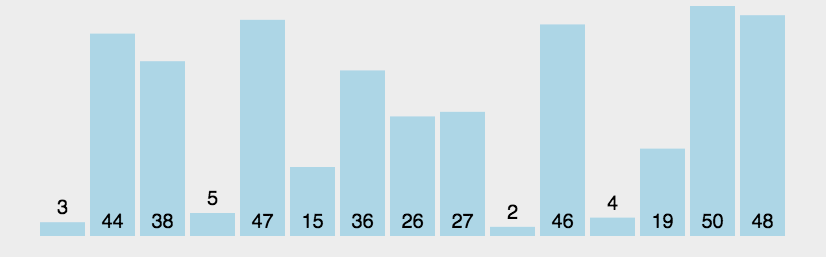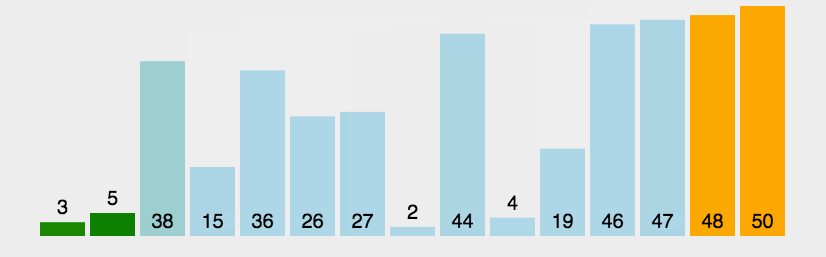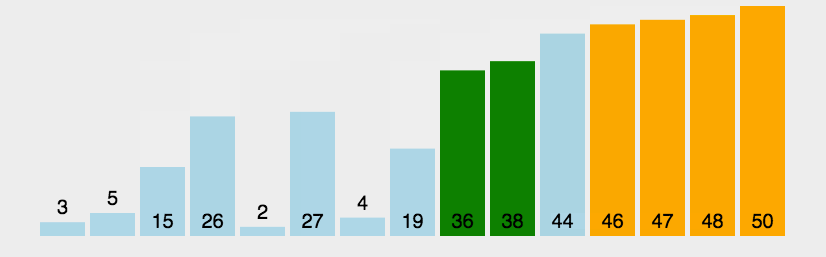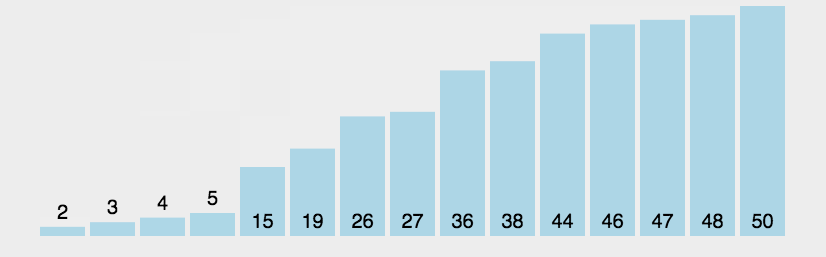十大排序算法总结
目录
- 总结
- 1. 快速排序
- 2. 冒泡排序
- 3. 插入排序
- 4. 堆排序
- 5. 归并排序
- 6. 选择排序
- 7. 基数排序
- 8. 希尔排序
- 9. 计数排序
- 10. 桶排序
- 算法比较:随机数案例
总结
依照本文所示顺序,进行了如下总结。在最后一节中,将通过生成五组随机数对每种算法的时效性进行测试。关于时间复杂度的介绍见:算法的时间复杂度。
| 序号 | 排序算法 | 代码复杂度 | 时间复杂度(平均) | 时间复杂度(最坏) | 空间复杂度 | 稳定性 |
|---|---|---|---|---|---|---|
| 1 | 快速排序 | ✩ | O ( n l o g 2 n ) O(nlog_2n) O(nlog2n) | O ( n 2 ) O(n^2) O(n2) | O ( n l o n g 2 n ) O(nlong_2n) O(nlong2n) | 不稳定 |
| 2 | 冒泡排序 | ✩ | O ( n 2 ) O(n^2) O(n2) | O ( n 2 ) O(n^2) O(n2) | O ( 1 ) O(1) O(1) | 稳定 |
| 3 | 插入排序 | ✩ | O ( n 2 ) O(n^2) O(n2) | O ( n 2 ) O(n^2) O(n2) | O ( 1 ) O(1) O(1) | 稳定 |
| 4 | 堆排序 | ✩✩✩ | O ( n l o g 2 n ) O(nlog_2n) O(nlog2n) | O ( n l o g 2 n ) O(nlog_2n) O(nlog2n) | O ( 1 ) O(1) O(1) | 不稳定 |
| 5 | 归并排序 | ✩✩ | O ( n l o g 2 n ) O(nlog_2n) O(nlog2n) | O ( n l o g 2 n ) O(nlog_2n) O(nlog2n) | O ( n ) O(n) O(n) | 稳定 |
| 6 | 选择排序 | ✩ | O ( n 2 ) O(n^2) O(n2) | O ( n 2 ) O(n^2) O(n2) | O ( 1 ) O(1) O(1) | 不稳定 |
| 7 | 基数排序 | ✩ | O ( n k ) O(nk) O(nk) | O ( n k ) O(nk) O(nk) | O ( n + k ) O(n+k) O(n+k) | 稳定 |
| 8 | 希尔排序 | ✩✩ | O ( n 1.3 ) O(n^{1.3}) O(n1.3) | O ( n 2 ) O(n^2) O(n2) | O ( 1 ) O(1) O(1) | 不稳定 |
| 9 | 计数排序 | ✩ | O ( n + k ) O(n+k) O(n+k) | O ( n + k ) O(n+k) O(n+k) | O ( n + k ) O(n+k) O(n+k) | 稳定 |
(以上表格部分数据引用自:Reference;本文使用 Python3 实现,需要 JavaScript 实现亦可点击上述链接)
1. 快速排序
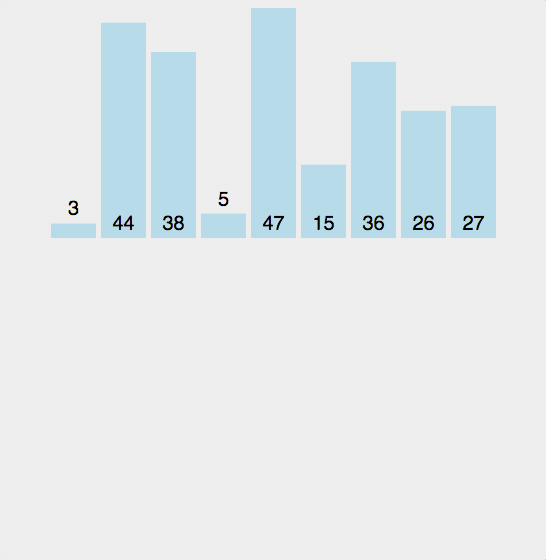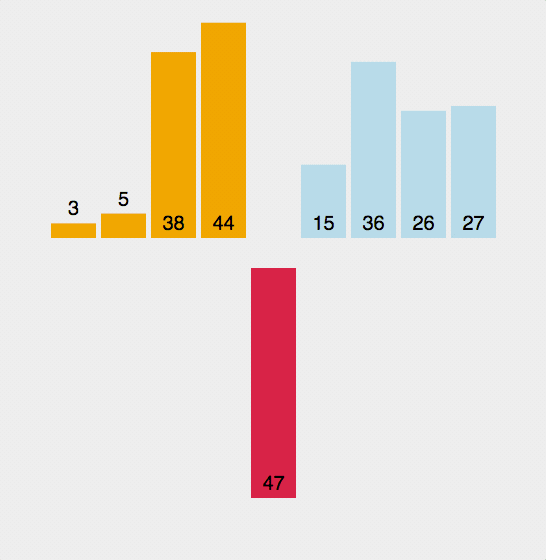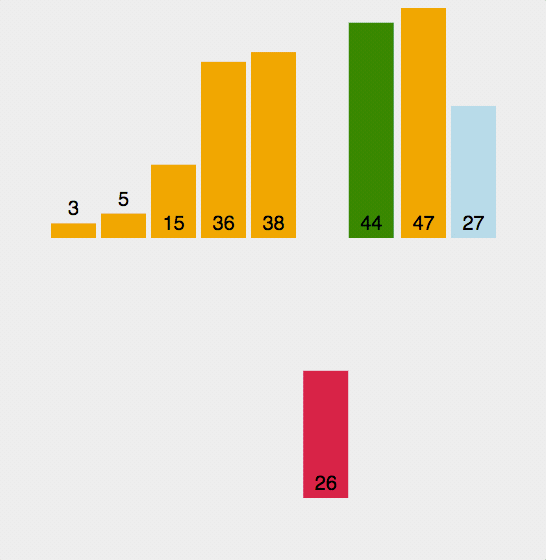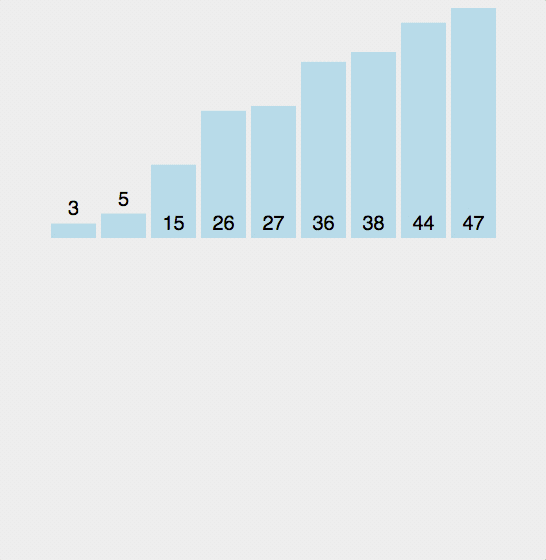
简称快排,核心思想在于递归。通过抽取数列中任意一个值作为基准 (Pivot),将全列分为三段,小于和大于该值的子数列使用同样的方法继续划分下去,直到分段只剩下一个数。
def quicksort(l):
if len(l) <= 1:
return l
else:
pivot = l[0] #基准
left_l = [x for x in l if x < pivot] #左段
mid_l = [x for x in l if x == pivot] #中间段
right_l = [x for x in l if x > pivot] #右段
return quicksort(left_l) + mid_l + quicksort(right_l) #递归
quicksort([8,5,3,4,1,2,6,7,9])
2. 冒泡排序
从第一个数开始,走访每一个后面出现的数,通过两两交换把较大的数往后推,直到走访过的数中最大的数被推到最后面,再开始第二轮;第二轮不再走访最后一个数,把剩下的数中最大的推到最后,也就是整个数列最大数的前面;以此类推。
def bubblesort(l):
for i in range(len(l)-1):
for j in range(len(l)-i-1): #不再走访前次循环排到数列最后的数
if l[j] > l[j+1]:
l[j], l[j+1] = l[j+1], l[j] #两两交换
return l
bubblesort([8,5,3,4,1,2,6,7,9])
3. 插入排序
从第二个数开始,走访每一个在此之前的数,找到合适的位置插入进去,并从原来的位置将该数删除。
def insertionsort(l):
for i in range(len(l)-1): #遍历每一个数
for j in range(i): #走访在此数之前的每一个数
if (l[j] <= l[i+1]) & (l[i+1] <= l[j+1]):
l.insert(j+1,l[i+1]) #插入该数
del l[i+2] #从原来位置删除
return l
insertionsort([8,5,3,4,1,2,6,7,9])
4. 堆排序
堆是从二叉树中走出来的一种数据结构,符合完全二叉树定义,除最后一层外其他每一层都被完全填充,并且所有结点都保持向左对齐;堆根据父节点和子节点的大小关系分为大根堆和小根堆,小根堆中父节点小于等于子节点,大根堆反之;堆排序是借助堆的数据结构设计的算法。例如,数列 [ 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 ] [1,2,3,4,5,6,7,8,9] [1,2,3,4,5,6,7,8,9] 的小根堆表示如下所示:

可以很轻易看出,两个子节点的位置分别为父节点下标 (n) 的 (2n) 和 (2n+1) ,这将是我们排序中需要利用的最关键的特性。关于堆的更多内容这里超出我们的文章讨论范围,暂时不介绍。Python 实现堆排序算法的步骤如下:
- 准备工作:在数列开头添加任意数值,以解决Python环境中初始下标为0的问题(该值不会参与排序)
- 第一步:通过自下往上遍历所有父节点,每次遍历以父节点和两个子节点中的最大值替换当前父节点,生成大根堆
- 第二步:取出这个大根堆的堆顶节点(全局最大值),与堆的最下最右的节点进行交换,然后剔除该最下最右的节点,用剩下的节点再构造出一个大根堆;重复以上步骤,直到新的大根堆长度为一,完成排序。
def adjust(l, start, end): #将当前堆转换为大根堆
temp = l[start]
i = start #调查父节点
j = start * 2 #第一个子节点
while j <= end:
if (j < end) and (l[j] < l[j + 1]): j += 1 #取数值更大的子节点
if temp < l[j]:
l[i] = l[j] #将该更大的值赋给父节点
i = j
j = j * 2
else:
break
l[i] = temp #将父节点初始值(最小值)赋给被替换的子节点
return l
def heapsort(l):
#准备工作
l = [0] + l #随意添加一个数
#第一步
max_upper = (len(l)-1)//2 #下标最大的父节点
for i in range(max_upper): #自下往上遍历每一个父节点
l = adjust(l, max_upper-i, len(l)-1) #层层替换
#第二步
for i in range(len(l)-2):
l[1], l[len(l)-1-i] = l[len(l)-1-i], l[1] #将堆顶节点和最下最右节点互换
l = adjust(l, 1, len(l)-i-2)
return [l[i] for i in range(1,len(l))]
heapsort([8,5,3,4,1,2,6,7,9])
5. 归并排序
与快速排序法类似,归并排序同样用到递归的思路,但归并排序直接对初始序列采取分治法(Divide & Conquer),将序列无限二分至所有子序列长度小于二,而后再根据划分顺序将排序结果一一合并。
def merge(left_l, right_l):
merged = []
a = b = 0
while a < len(left_l) and b < len(right_l):
if left_l[a] < right_l[b]:
merged.append(left_l[a])
a += 1
else:
merged.append(right_l[b])
b += 1
merged += left_l[a:]
merged += right_l[b:]
return merged
def mergesort(l):
if len(l) <= 1:
return l
mid = len(l)//2
left_l = mergesort(l[:mid])
right_l = mergesort(l[mid:])
return merge(left_l, right_l)
mergesort([8,5,3,4,1,2,6,7,9])
6. 选择排序
从第一个数开始遍历至最后一个数,找到最小值与第一个数互换;然后从第二个数开始遍历,找到最小值与第二个数互换;以此类推。
def selectionsort(l):
for i in range(len(l)): #从头开始遍历
min_index = i
min_value = l[i]
for j in range(len(l)-i-1): #走访此数之后的每一个数
if l[i+j+1] < min_value:
min_index = i+j+1 #记录最小值下标
min_value = l[min_index] #记录最小值
l[i], l[min_index] = l[min_index], l[i] #位置互换
return l
selectionsort([8,5,3,4,1,2,6,7,9])
7. 基数排序
第一轮,按所有数的个位数,将数分类放进0-9的槽中;第二轮,将槽中的数从0到9按顺序取出,再从第一个开始重新按顺序根据十位数放进槽中;以此类推,最大的数有多少位,则进行多少次迭代。
def radixsort(l):
for k in range(4): #从个位数开始排序
boxes = [[] for _ in range(10)] #新建槽位
for i in l:
boxes[int(i/(10**k)%10)].append(i) #放入对应槽中
l = [num for box in boxes for num in box] #将数按顺序取出
return l
radixsort([8,5,3,4,1,2,6,7,9])
8. 希尔排序
又称为缩小增量排序,是针对插入排序算法进行改良后的成果。首先将序列分为若干行(专业名为增量分组),对每一列进行直接插入排序;排序完成后,将行数按一定整数加倍进行序列重组,而后对新的列重新进行插入排序;以此类推,直到每行(每个增量分组)仅剩一个数,排序完成。以初始划分为两行为例,第一次排序:(右下角括号为 Python 索引下标)
 第二次排序:
第二次排序: 第三次排序步长调整为 1,每行仅剩一个数,排序完成则为最终排序结果。
第三次排序步长调整为 1,每行仅剩一个数,排序完成则为最终排序结果。
def shellsort(l):
step = len(l)//2
while step > 0:
for i in range(step,len(l)): #从第二行第一个数开始,进行列排序
while (i >= step) & (l[i] < l[i-step]):
l[i],l[i-step] = l[i-step],l[i]
i -= step
step = step // 2 #缩小步长,增加行数,进行下一次迭代
return l
shellsort([8,5,3,4,1,2,6,7,9])
9. 计数排序
从数列中的最小值开始,直到最大值,统计每个整数出现的频率,而后按数值从小到大生成一条新的序列。计数排序要求数列中不能出现浮点小数,且当极差过大时,内存占用是灾难性的。
def countingsort(l):
sort = []
for i in range(max(l)+1): #从0开始遍历至最大值
sort += [i]*l.count(i) #根据整数的频率在新数列中相应添加
return sort
countingsort([8,5,3,4,1,2,6,7,9])
10. 桶排序
桶排序是在计数排序的基础上衍生出来的排序思想,没有特定的实施步骤,它摒弃计数排序中占用过大空间的整数计频方法,要求使用者采用更高效的办法对数据进行映射,分到有限个的桶中,使用任意算法对非空桶中的数进行排序后,对所有数进行汇总。笔者这里使用求自然对数后取整的方法将 1 至 20000 的数投入到 0 - 9 十个桶中,对桶中的数进行选择排序。
import math
def selectionsort(l): #与上文中的选择排序代码相同
for i in range(len(l)): #从头开始遍历
min_index = i
min_value = l[i]
for j in range(len(l)-i-1): #走访此数之后的每一个数
if l[i+j+1] < min_value:
min_index = i+j+1 #记录最小值下标
min_value = l[min_index] #记录最小值
l[i], l[min_index] = l[min_index], l[i] #位置互换
return l
def bucketsort(l):
buckets = [[] for _ in range(10)] #建桶
for i in l:
buckets[int(math.log(i+1))].append(i) #分桶
return [num for bucket in buckets for num in selectionsort(bucket)] #汇总
bucketsort([8,5,3,4,1,2,6,7,9])
算法比较:随机数案例
用以下代码分别生成五组随机数,对除桶排序以外的所有排序算法进行测试:
import random
params = ((10,1e4),(10,1e5),(100,1e4),(1000,1e4),(10000,1e4))
for param in params:
print('\nMax_Value %d, Length %d:'%(param[0],param[1]))
l = [random.randint(1,param[0]) for _ in range(param[1])] #生成随机数
for sort_func in [quicksort,bubblesort,insertionsort,heapsort,mergesort,
selectionsort,radixsort,shellsort,countingsort,bucketsort]: #遍历每一种算法
start = time()
sort_func(l); #模拟运行
end = time()
print('%s \t%.6fs'%(sort_func,end-start))
测试结果如下:
| 序号 | 排序算法 | [ 10 ] × 1 0 3 [10]\times10^3 [10]×103 | [ 10 ] × 1 0 5 [10]\times10^5 [10]×105 | [ 1 0 2 ] × 1 0 3 [10^2]\times10^3 [102]×103 | [ 1 0 3 ] × 1 0 3 [10^3]\times10^3 [103]×103 | [ 1 0 4 ] × 1 0 3 [10^4]\times10^3 [104]×103 |
|---|---|---|---|---|---|---|
| 1 | 快速排序 | 0.000496s | 0.002976s | 0.000991s | 0.001488s | 0.018814s |
| 2 | 冒泡排序 | 0.067956s | 6.287795s | 0.061465s | 0.066464s | 7.055603s |
| 3 | 插入排序 | 0.098705s | 16.901715s | 0.082337s | 0.081344s | 8.364087s |
| 4 | 堆排序 | 0.001984s | 0.026784s | 0.002480s | 0.001984s | 0.028768s |
| 5 | 归并排序 | 0.002976s | 0.037209s | 0.002976s | 0.003472s | 0.039184s |
| 6 | 选择排序 | 0.040174s | 4.224440s | 0.041166s | 0.043683s | 4.444198s |
| 7 | 基数排序 | 0.001984s | 0.016369s | 0.001488s | 0.001488s | 0.016864s |
| 8 | 希尔排序 | 0.000992s | 0.019840s | 0.002480s | 0.002480s | 0.045137s |
| 9 | 计数排序 | 0.000496s | 0.001488s | 0.001488s | 0.013392s | 1.305474s |
| 10 | 桶排序 | 0.015376s | 1.764807s | 0.012400s | 0.016864s | 1.461186s |
由以上结果可见,快速排序和基数排序在大批量和大额整数的排序上表现更为优异和稳定。