堆排序极简思想

1、构建大（小）顶堆

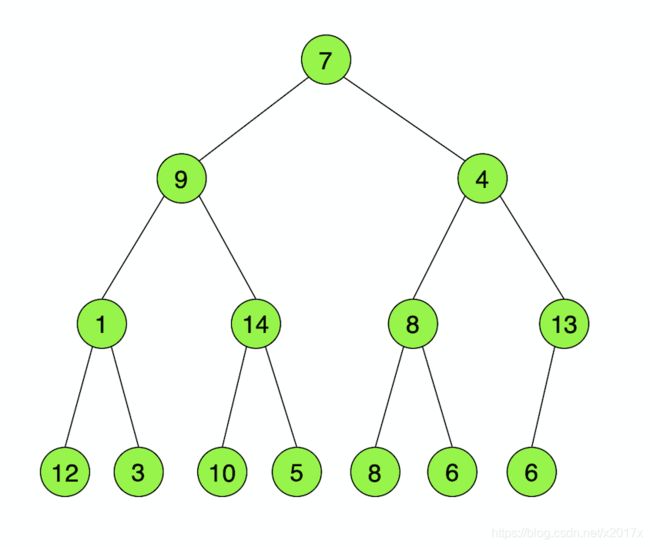
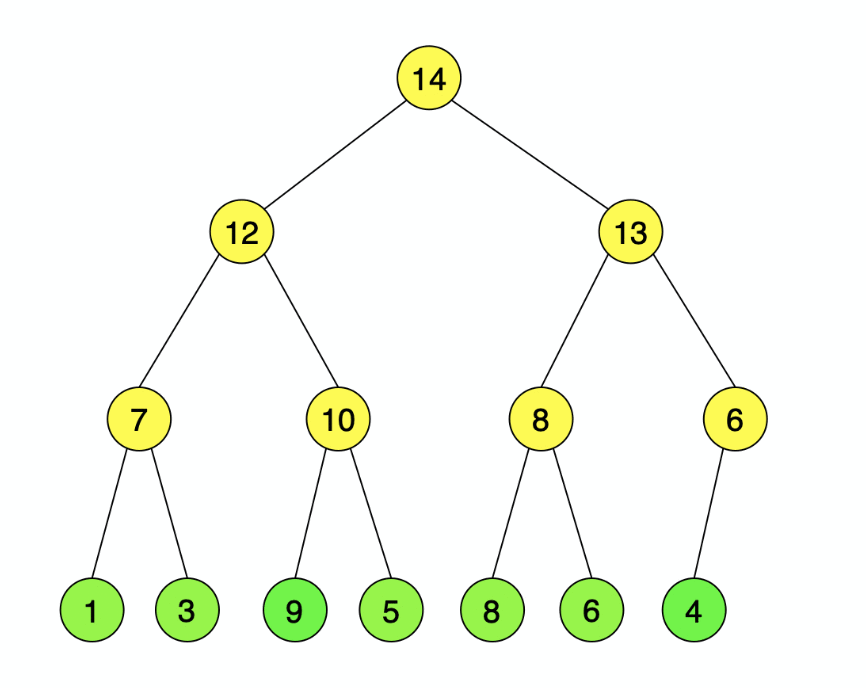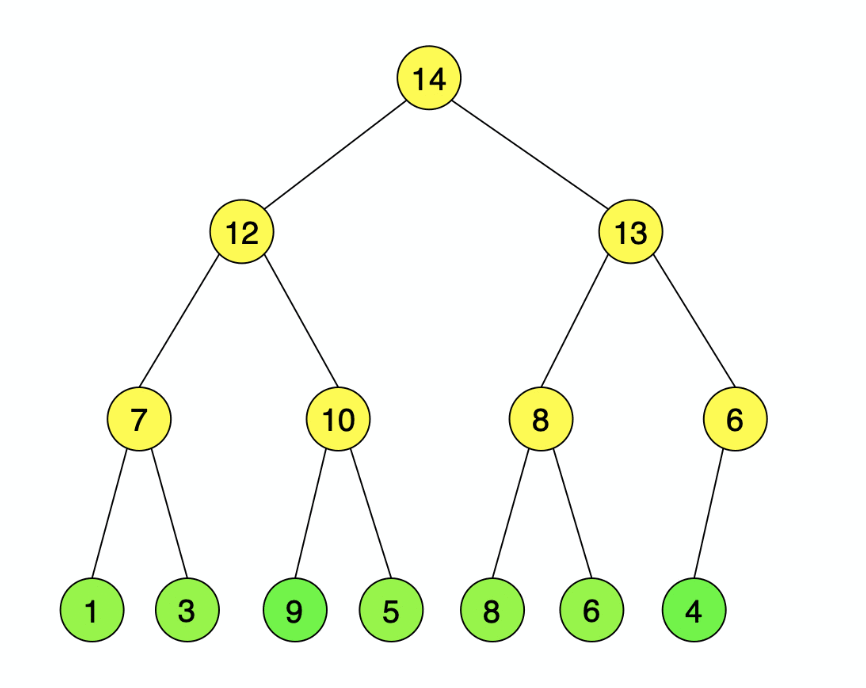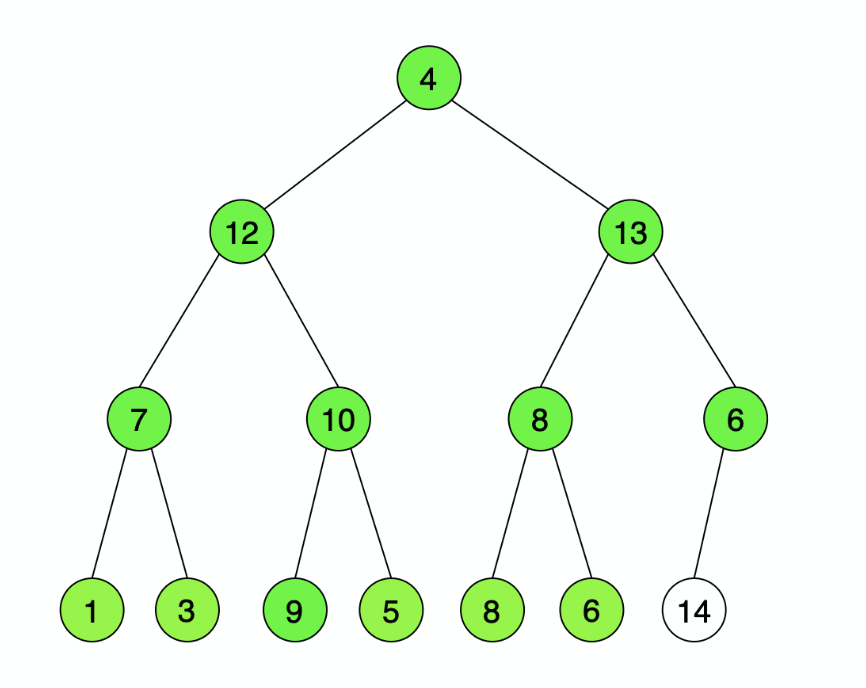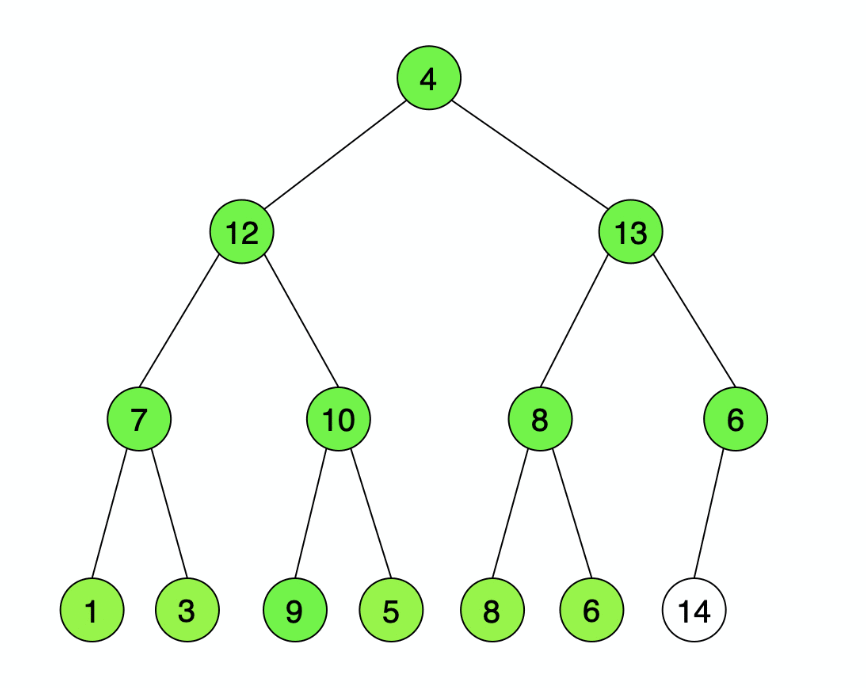
      以上是一个大顶堆示意图（后续均以大顶堆为示例），用完全二叉树来表示，每个根节点的值均不小于其左右子节点（如果有左右子节点）的值。使用完全二叉树可以简化我们的代码，完全不用使用其它的数据结构，用数组表示就足够了，规则就是以深度遍历顺序存储（上图存储即为{14,12,13,9,7,10,8,1,3,4,5,8,6,6}，下图则为{7,9,4,1,14,8,13,12,3,10,5,8,6,6}），设数组初始下标为0，父子节点下标关系为：左孩子下标=父亲下标*2+1，右孩子下标=父亲下标*2+2，父亲下标=（左/右孩子下标-1）/2。

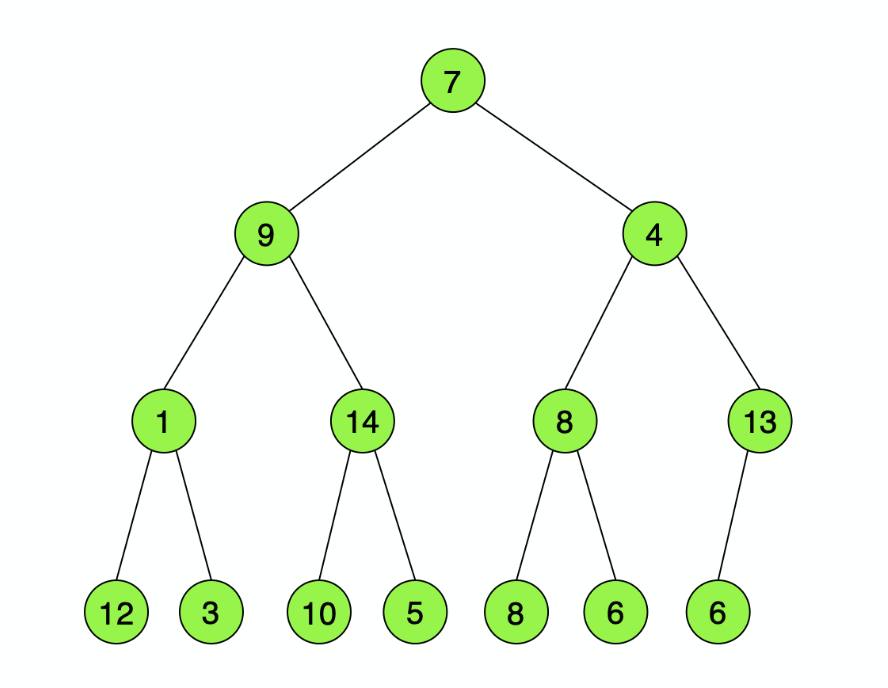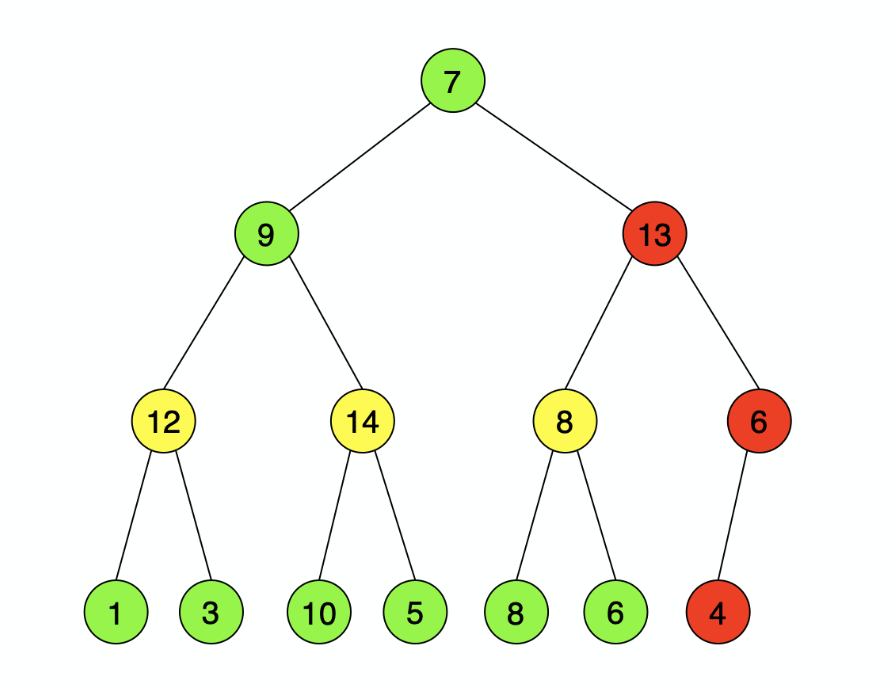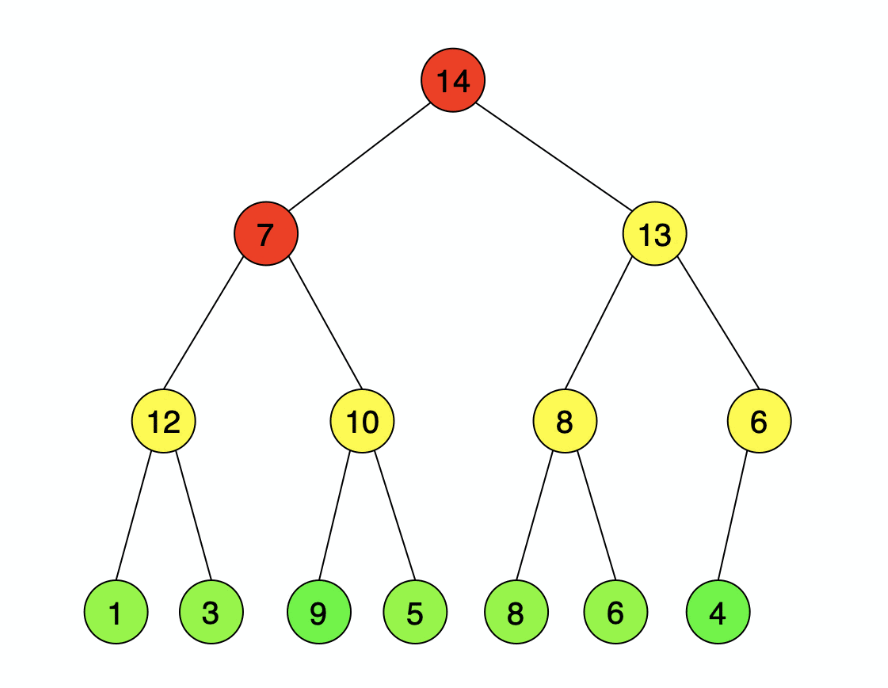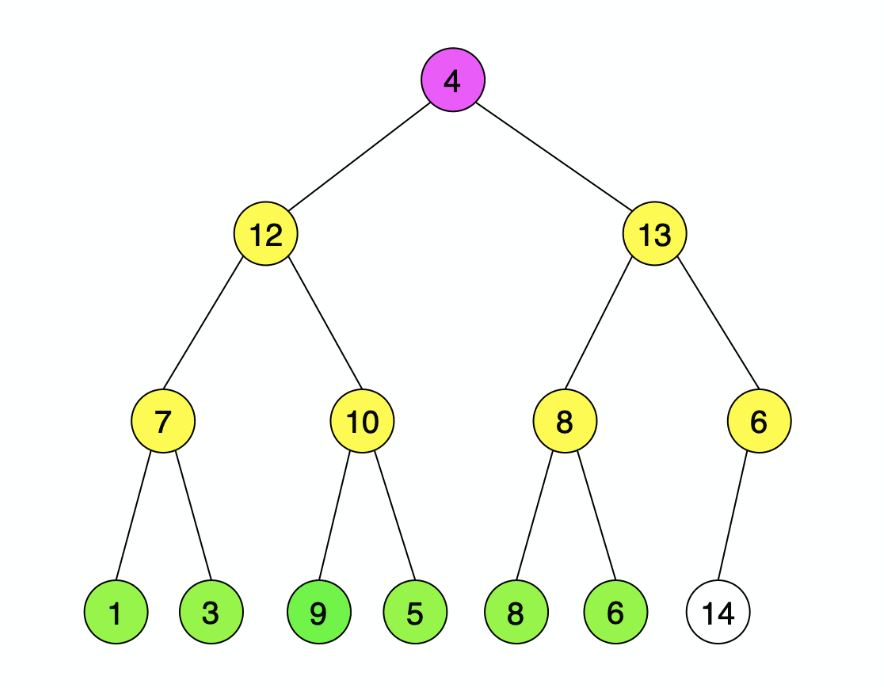
       构建大顶堆：核心思想就是保证根节点不小于左右孩子，且左右子树均为大顶堆。对于无孩子的节点，我们认定为其本身就是一个大顶堆，因此从最后一个有孩子的节点（上图13）开始（其子树均为大顶堆），对以该节点为根的树“调整为大顶堆（注意：其子树均为大顶堆）”，依次向前遍历（根节点13 8 14 1 4 9 7），直至最终的根节点。由于先遍历的子节点，因此可以保证每个根节点被遍历到时均能满足子树为大顶堆，so，我们的核心问题就是“调整为大顶堆（其子树均为大顶堆）”，后面你会发现这将是整个堆排序的核心。把这个核心问题简化为一个函数(adjust()下面讲到)，我们要做的就是从最后一个有孩子的节点向前遍历调用adjust()就好了，最后一个有孩子的节点也就是数组最后一个节点的父节点。

       “调整为大顶堆（其子树均为大顶堆）”：核心思想就是保证根节点不小于左右孩子，且左右子树均为大顶堆。从根节点开始比较其与左右孩子的值，如果根节点本身最大或没有左右孩子，则结束，如果左孩子（右孩子同理）最大，则交换根节点值与左孩子值，对左子树进行操作“调整为大顶堆（其子树均为大顶堆）”，如此递归即可。

       下图为构建大顶堆的过程，形成的大顶堆序列为{14,12,13,7,10,8,6,1,3,9,5,8,6,4}。

2、将堆顶元素与堆尾未排好序的元素交换

       大顶堆构建好了，大顶堆对于排序最有意义的一点就是堆顶为该堆的最大值，我们要的就是这个最大值，因此将堆顶元素的值与堆尾元素交换，将目前的最大值存储到数组的最后，保证数组的最后为目前堆的最大值，即已排序好的数组。以下{14}即为已排好序的数列。接下来的处理要针对数组{4,12,13,7,10,8,6,1,3,9,5,8,6}了。

3、将被打乱的堆调整为大顶堆

       刚才把堆尾的元素放到了堆顶，好不容易构建的大顶堆，你又给我破坏了。别急，我们要做的就是被破坏的再恢复回去，基于上面一步，现在我们要处理的堆是出去上一步中被放到已排序号的数组中的那个元素，也就是少了一个元素。既然那个最大值被驱出族群，那么剩下的这个堆只有根节点不是最大堆，其千千万万子堆还是最大堆对不对。因此我们的当务之急就是对根节点进行“调整为大顶堆（其子树均为大顶堆）”操作，仅对根节点调用一次adjust()即可。

4、循环步骤2和3

       操作一次步骤2、3，就完成了一个元素的排序，循环n-1遍（n为数组个数）就完成了n-1元素的排序，最后留下的肯定是最小的了，结束。

 

下面给出C++实现：

#include
using namespace std;

void heapsort(int* a, int n);
void swap(int& a,int& b);


int main()
{
    int n;
    cin>>n;
    int* a = new int[n];
    for(int i=0;i>a[i];
    cout<a[m])
    {
        swap(a[m*2+1],a[m]);
        adjust(a, n, m*2+1);
    }
    if(m*2+2a[m])
    {
        swap(a[m*2+2],a[m]);
        adjust(a, n, m*2+2);
    }
}

void heapsort(int* a, int n)
{
    for(int i = ((n-1)-1)/2;i>=0;--i)
        adjust(a,n,i);
    
    for(int i=n-1;i>0;--i)
    {
        swap(a[0],a[i]);
        adjust(a, i, 0);
    }
    return;
}