分享几道前端面试高频算法题~
下面我会列举数组排序、斐波那契数列、数组去重、数组扁平化、输出一个正数n,要求输出所有和为n的连续正整数序列这几种算法题的几种实现解法~
我比较着重讲的是算法思想,尽量通俗易懂,看了真香系列~
目录
- 一、数组排序
-
- 1. 冒泡排序
- 2. 插入排序
- 3. 快速排序
- 二、斐波那契数列
- 三、数组去重
-
- 1. 方案一:利用ES6新特性:Set集合
- 2. 方案二:利用includes/indexof
- 3. 方案三:利用正则分组的引用,来处理相邻项
- 四、数组扁平化
-
- 1. 方案一:利用ES6新特性:flat方法
- 2. 方案二:循环数组
- 五、输入一个正数n,要求输出所有和为n的连续正整数序列
一、数组排序
1. 冒泡排序
- 将数组当前项与后一项对比,如果比后一项大,则交换位置
- 每比较一轮都会把一个最大的值放在数组的末尾,以此递增;
举个简单的例子,数组[5,4,3,2,1]
第一轮比较,变为了[4,3,2,1,5],一共比较了四次
第二轮比较,变为了[3,2,1,4,5],一共比较了三次(无需和最后一项对比,因为上一轮已经把该数组中最大的数放到了末尾)
第三轮比较,变为了[2,1,3,4,5],一共比较了两次
第四轮比较,变为了[1,2,3,4,5],一共比较了一次,结束~
显而易见,一共需要两次for循环,上面这种说的还是最坏的一种情况。另外例举一种最好的情况,数组[1,2,3,4,5],第一轮比较的时候,结果是无需交换任何值,这意味着,以后的每一轮比较,都是无需交换值的,因为此时数组已经排好序了;数组[2,1,3,4,5],也是同理,第一轮比较后,交换了一次值,变为了[1,2,3,4,5],第二轮比较后,同样发现无需交换值,此时我们可以直接结束循环,返回结果了。
Array.prototype.bubble = function () {
let _this = this,
n = _this.length,
flag = false;// 优化
// 控制比较多少轮
for (let i = 0; i < n - 1; i++) {
// 每轮比较多少次
for (let j = 0; j < n - 1 - i; j++) {
// 当前项与后一项对比,如果比后一项大,则交换位置
if (_this[j] > _this[j + 1]) {
[_this[j], _this[j+1]] = [_this[j+1], _this[j];
flag = true;
}
}
if (!flag) break;
flag = false;
}
return _this;
}
const arr = [2, 1, 4, 6, 17, 5, 3, 88, 34];
console.log(arr.bubble());
2. 插入排序
举个形象的例子,就像抓牌一样,先抓一张牌放在手里
- 再抓一张牌进来,如果新抓的牌(假设从后往前比)比前面的牌大,则插在后面
- 如果比前面的牌小,则继续往前进一步,再次与它前面的牌比较
- 如果比到头一张牌(尽头)了,还是没有前面的牌小,则放在数组开头
Array.prototype.insert = function () {
let _this = this,
n = _this.length,
ary = [];
ary.push(_this[0]);
for (let i = 1; i < n; i++) {
for (let j = ary.length - 1; j >= 0; j--) {
if (_this[i] > ary[j]) {
ary.splice(j + 1, 0, _this[i]);// 在位置j后面插入_this[i]
break;
}
if (j === 0) ary.unshift(_this[i])
}
}
return ary;
}
const arr = [2, 1, 4, 6, 17, 5, 3, 88, 34];
console.log(arr.insert());
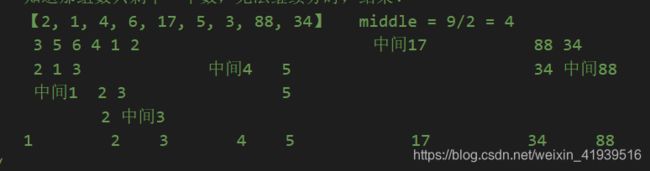
3. 快速排序
这里是用到二分法(递归实现)
- 取数组的中间数(向下取整)
- 分成左右两组数——比中间数小的放左边,比中间大的放右边
- 然后左边那组数,继续取中间数,依旧是分成左右两组数。。。右边也是
- 以此递推————————
- 直到那组数只剩下一个数,无法继续分时,结束!
下面这种图是这种思想的一个图(看不懂就跳过把,毕竟这种图有丢丢潦草)
Array.prototype.middle = function () {
let _this = this,
middle = Math.floor(_this.length / 2);// 当数组不可再分时,结束递归(即数组长度为1时)
if (middle === 0) return _this;
let left = [],
right = [];
for (let i = 0; i < _this.length; i++) {
if (i === middle) continue;
_this[i] < _this[middle] ? left.unshift(_this[i]) : right.push(_this[i]);
}
return left.middle().concat(_this[middle], right.middle());
}
const arr = [2, 1, 4, 6, 17, 5, 3, 88, 34];
console.log(arr.middle());
二、斐波那契数列
什么是斐波那契数列呢?这种数组的特点就是:数组前两项为1,后面每一项的值都是自己前两项的值的和,例如它~
[1,1,2,3,5,8,13,21....]
如何输出该数列中下标为n的数呢?
下面我例举了两种方案,第一种超级好理解,一看就会那种~
- 先初始化数组
[1,1],每次前两项相加的值添加到该数组中 - 假设n =5,则说明数组有6(5+1)个数,需要添加4(5+1-2)个数进去,每增加一次则需要遍历一次。
- -遍历结束后,返回数组的最后一项的值
边看着代码理解吧~
function feibonaqi(n) {
let arr = [1, 1];
// 循环多少次 n+1-2次
for (let i = 0; i < n + 1 - 2; i++) {
arr.push(arr[arr.length - 2] + arr[arr.length - 1])
}
return arr[arr.length - 1]
}
console.log(feibonaqi(5));
第二种方案是递归实现的~
function feibonaqi(n) {
if (n === 0 || n === 1) {
return 1;
}
return feibonaqi(n - 1) + feibonaqi(n - 2);
}
三、数组去重
网络上数组去重的算法数不胜数,但归根到底,都是那几种思想,这里我列出三种方案,看完这三种方案,你同样也可以写出“关于数组去重的n种算法”~
1. 方案一:利用ES6新特性:Set集合
Set 是无序不可重复的多个value的集合体,重复的元素在Set中自动被过滤掉。
注意:Set返回的数据类型是"object"
console.log(typeof new Set([1,2,3,3,2]));//object
let arr = [1, 2, 4, 5, 2, 3, 4, 6, 7, 7, 8, 1];
let ary = Array.from(new Set(arr)); // 将数据类型转换为数组类型
//==============================
// 或者这样子做也可以将数据类型转换为数组类型
let ary = [...new Set(arr)];//利用es6的拓展运算符,将一个数组转为用逗号分隔的参数序列
2. 方案二:利用includes/indexof
这种思想呢,就是遍历原数组,通过includes/indexof来查看是否有重复元素。
(1)新建一个数组来装。遍历原数组,如果在新数组中没有找到正在遍历的元素,则添加进去
let arr = [1, 2, 4, 5, 2, 3, 4, 6, 7, 7, 8, 1];
let ary = [];
for (let i = 0; i < arr.length; i++) {
// if(ary.indexOf(arr[i]) === -1) ary.push(arr[i])
if(!ary.includes(arr[i])) ary.push(arr[i])
}
console.log(ary);
(2)删除原来数组的重复项。遍历原数组,如果有重新项,则删除。但这样子做容易有数组塌陷的问题,注意哦!
let arr = [1, 2, 4, 5, 2, 3, 4, 6, 7, 7, 8, 1];
for(let i = 0;i<arr.length;i++){
if(arr.indexOf(arr[i]) !== i){
arr.splice(i,1);
i--;// 防止数组塌陷,缺点就是每次只要有重复项,该项后面的所有元素的下标都要重新排一遍
}
}
console.log(arr)
另外一种解决数组塌陷的方式,如下~
let arr = [1, 2, 4, 5, 2, 3, 4, 6, 7, 7, 8, 1];
for(let i = 0;i<arr.length;i++){
if(arr.indexOf(arr[i]) !== i){
arr[i] = null;// 把重复项赋值为null
}
}
// 再遍历一次数组,把null值的元素剔除掉
arr = arr.filter(item =>item !== null);// 如果省略{}就可以省略return
console.log(arr)
3. 方案三:利用正则分组的引用,来处理相邻项
首先就是将数组排序,这样子重复的项自然会相邻,利用repalce的正则捕获就可以完成了。这里如果不了解replace里面回调函数的运行机制的孩纸,可以去补补正则的功课哈~
let arr = [1, 2, 4, 5, 2, 3, 4, 6, 7, 7, 8, 1];
arr.sort((a,b)=>a-b);
arr = arr.join('@')+'@';
let reg = /(\d+@)\1*/g,
ary=[];
// 匹配几次,回调函数就执行几次,
arr.replace(reg,(current,arg)=>ary.push(Number(arg.slice(0,arg.length-1))))
console.log(ary)
四、数组扁平化
例如[1,2,3,4,5]就是一维数组,下面这个是四维数组
let arr = [ // 这是个四维数组
[1, 2, 3, 4, 6],
22,
[1, 2, 3, [1, 1, 4, 5], [8, 9, 7, [1, 2, 3, 4, 77, 24], 6, 6, 5]]
]
扁平化就是把数组”降维“降到一维的意思~
实现数组扁平化同样也有很多方法,这里也是例举几种~
1. 方案一:利用ES6新特性:flat方法
es6里面数组原型的flat方法,可以实现扁平化
arr.flat(n); //arr数组扁平化n级
arr = arr.flat(Infinity);//将数组扁平化无穷极,也就是直接到一维数组啦
2. 方案二:循环数组
(1)
while (arr.some(item => Array.isArray(item))) {// 只有有任意一个元素是数组
arr = [].concat(...arr)
}
(2) 利用递归实现~
只要里面的元素有一个是数组类型的,就继续循环该元素,直到循环的数组的元素没有数组类型为止,返回该元素
function flat() {
let ary = [],
_this = this;
let fn = (arr) => {
for (let i = 0; i < arr.length; i++) {
if (arr[i] instanceof Array) {
fn(arr[i]);
continue;
}
ary.push(arr[i]);//把不是数组的元素放到新数组里面去
}
}
fn(_this);
return ary;
}
Array.prototype.flat = flat;
console.log(arr.flat())
五、输入一个正数n,要求输出所有和为n的连续正整数序列
例如,输入15,输出[ [ 1, 2, 3, 4, 5 ], [ 4, 5, 6 ], [ 7, 8 ] ]
解题思想就是——先算出该正数的中间数(向上取整),因为数列最大的数不可能超过这个数。
例如15的中间数为8,8+9就肯定会超过15,所以输出结果里面序列的数字一定是1~8之间的,那么我们就在这个区间进行判断即可
直接上代码把~
// 创建一组a-b之间的连续正数数组
function createArr(a, b) {
// let arr =[];
// for(let i = a;i<=b;i++){
// arr.push(i);
// }
// return arr;
return new Array(b - a + 1).fill(null).map(item => item = a++)
}
function fn(n) {
let middle = Math.ceil(n / 2);// 该序列最大的数不超过这个数
let arr = [],
sum = 0;
for (let i = 1; i <= middle; i++) {
sum = 0;
for (let j = i; j <= middle; j++) {
sum += j;
if (sum === n) {
arr.push(createArr(i, j));
break;
}
if (sum > n) {
break;
}
}
}
return arr;
}
console.log(fn(15))
能看到这里的你,一定很棒!!