博弈论基础知识与SG函数

写在前面：本文很长，若有兴趣，请耐心阅读。

简介

博弈论，又称为对策论（Game Theory）、赛局理论等。博弈论主要研究公式化的激励结构间的相互作用，是研究具有斗争或竞争性质现象的数学理论和方法。 博弈论考虑游戏中的个体的预测行为和实际行为，并研究它们的优化策略。

要素

1.局中人：在一场竞赛或博弈中，每一个有决策权的参与者成为一个局中人。只有两个局中人的博弈现象称为两人博弈,而多于两个局中人的博弈称为多人博弈。

2.策略：一局博弈中，每个局中人都有选择实际可行的完整的行动方案，即方案不是某阶段的行动方案，而是指导整个行动的一个方案，一个局中人的一个可行的自始至终全局筹划的一个行动方案，称为这个局中人的一个策略。如果在一局博弈中局中人都总共有有限个策略，则称为有限博弈 ，否则称为无限博弈。

3.得失：一局博弈结局时的结果称为得失。每个局中人在一局博弈结束时的得失，不仅与该局中人自身所选择的策略有关，而且与全局中人所取定的一组策略有关。所以，一局博弈结束时每个局中人的“得失”是全体局中人所取定的一组策略的函数，通常称为支付（payoff）函数。

4.对于博弈参与者来说，存在着一个博弈结果的结合。

5.博弈涉及到均衡：均衡是平衡的意思，在经济学中，均衡意即相关量处于稳定值。在供求关系中，某一商品市场如果在某一价格下，想以此价格买此商品的人均能买到，而想卖的人均能卖出，此时我们就说，该商品的供求达到了均衡。所谓纳什均衡，它是一种稳定的博弈结果。

博弈论研究的假设：
决策主体是理性的，最大化自己的利益；
完全理性是共同知识；
每个参与人被假定为对所处环境及其他参与者的行为形成正确信念与预期。

博弈的类型

博弈的分类根据不同的基准也有不同的分类。

1.合作博弈 和 非合作博弈

合作博弈和非合作博弈的区别在于相互发生作用的当事人之间有没有一个具有约束力的协议，如果有，就是合作博弈，如果没有，就是非合作博弈。

2.静态博弈 和 动态博弈

从行为的时间序列性，博弈可以进一步分为静态博弈、动态博弈两类：
①静态博弈 是指在博弈中，参与人同时选择或虽非同时选择但后行动者并不知道先行动者采取了什么具体行动；
②动态博弈 是指在博弈中，参与人的行动有先后顺序，且后行动者能够观察到先行动者所选择的行动。

3.完全信息博弈 和 不完全信息博弈

按照参与人对其他参与人的了解程度分为完全信息博弈和不完全信息博弈。
①完全信息博弈 是指在博弈过程中，每一位参与人对其他参与人的特征、策略空间及收益函数有准确的信息。
②不完全信息博弈 是指如果参与人对其他参与人的特征、策略空间及收益函数信息了解的不够准确、或者不是对所有参与人的特征、策略空间及收益函数都有准确的信息，在这种情况下进行的博弈就是不完全信息博弈。

博弈论还有很多分类，比如：以博弈进行的次数或者持续长短可以分为有限博弈和无限博弈；以表现形式也可以分为一般型（战略型）或者展开型；以博弈的逻辑基础不同又可以分为传统博弈和演化博弈。在此不做过多说明。

纳什均衡

纳什均衡(Nash Equilibrium)：在一策略组合中，所有的参与者面临这样一种情况，当其他人不改变策略时，他此时的策略是最好的。也就是说，此时如果他改变策略他的支付将会降低。

在纳什均衡点上，每一个理性的参与者都不会有单独改变策略的冲动。

纳什均衡点存在性证明的前提是 博弈均衡偶 概念的提出。所谓“均衡偶”是在二人零和博弈_{（零和博弈，又称零和游戏，是博弈论的一个概念，指参与博弈的各方，在严格竞争下，一方的收益必然意味着另一方的损失，博弈各方的收益和损失相加总和永远为“零”，双方不存在合作的可能。）}中，当局中人A采取其最优策略a*，局中人B也采取其最优策略b*,如果局中人B仍采取b*，而局中人A却采取另一种策略a，那么局中人A的支付不会超过他采取原来的策略a*的支付。这一结果对局中人B亦是如此。

这样，“均衡偶”的明确定义为：一对策略a和策略b称之为均衡偶，对任一策略a和策略b，总有：偶对(a, b*) ≤ 偶对(a*,b*) ≥偶对(a*,b)。

对于非零和博弈也有如下定义：一对策略a和策略b称为非零和博弈的均衡偶，对任一策略a和策略b，总有：
对局中人A的偶对（a, b*） ≤偶对(a*,b*);
对局中人B的偶对（a*，b）≤偶对(a*,b*)。

有了上述定义，就立即得到纳什定理：

任何具有有限纯策略的二人博弈至少有一个均衡偶。这一均衡偶就称为纳什均衡点。

纳什定理的严格证明要用到不动点理论，不动点理论是经济均衡研究的主要工具。通俗地说，寻找均衡点的存在性等价于找到博弈的不动点。

纳什均衡点概念提供了一种非常重要的分析手段，使博弈论研究可以在一个博弈结构里寻找比较有意义的结果。但纳什均衡点定义只局限于任何局中人不想单方面变换策略，而忽视了其他局中人改变策略的可能性，因此，在很多情况下，纳什均衡点的结论缺乏说服力，研究者们形象地称之为“天真可爱的纳什均衡点”。

塞尔顿（R·Selten)在多个均衡中剔除一些按照一定规则不合理的均衡点，从而形成了两个均衡的精炼概念：子博弈完全均衡和颤抖的手完美均衡。(至于这到底都是些什么，不用管它)

经典案例一

囚徒困境
在博弈论中，“囚徒困境”（prisoner’s dilemma）是较为经典的博弈模型。该模型用一种特别的方式为我们讲述了一个警察与小偷的故事。
假设有两个小偷A和B被警察抓住。警方将两人分别置于不同的两个房间内进行审讯，对每一个犯罪嫌疑人，警方给出的政策是：如果两个犯罪嫌疑人都坦白了罪行，两人都被判有罪，各被判刑8年；如果只有一个犯罪嫌疑人坦白，另一个人抵赖，则抵赖者判刑10年，坦白者立即释放。如果两人都抵赖，则各判型1年。下表给出了这个博弈的支付矩阵。

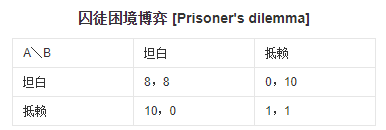
对A来说，尽管他不知道B作何选择，但他知道无论B选择什么，他选择“坦白”总是最优的。对于B而言亦是如此，结果是两人都被判刑8年。但是，倘若他们都选择“抵赖”，每人只被判刑1年。

在上表中的四种行动选择组合中，（抵赖、抵赖）是最优最有选择，因为这以外的任何选择都至少会使一个人的境况变差。但是，“坦白”是每一个犯罪嫌疑人个人的最优战略，而（坦白，坦白）是一个最优战略均衡，即纳什均衡。

不难看出，两者之间存在冲突。

从数学角度讲，这个理论是合理的，也就是都选择坦白。但从心理学角度讲，选择坦白的成本会更大，一方坦白害得另一方加罪，那么事后的报复行为以及他将来可能受到的损失会更多。

经典案例二

美女的硬币
一位陌生美女主动过来和你搭讪，并要求和你一起玩个游戏。美女提议：“让我们各自亮出硬币的一面，或正或反。如果我们都是正面，那么我给你3元，如果我们都是反面，我给你1元，剩下的情况你给我2元就可以了。”听起来不错的提议，但是这个游戏真的够公平吗？

男士/美女	女正面	女反面
男正面	3，-3	-2，2
男反面	-2，2	1，-1

假设男士出正面的概率是$x$，反面的概率是$1-x$。为了使利益最大化，应该在对手出正面或反面的时候我们的收益都相等，不然对手总是可以改变正反面出现的概率让我们的总收入减少，由此列出方程就是$$3x+(-2)\ast (1-x)=(-2)\ast x+1\ast (1-x)$$
解方程得$x=\frac{3}{8}$，也就是说平均每八次出示3次正面，5次反面是我们的最优策略。而将$x=\frac{3}{8}$代入到收益表达式 $3\ast x+(-2)\ast (1-x)$中 就可得到每次的期望收入，计算结果是$-\frac{1}{8}$元。

同样，设美女出正面的概率是y，反面的概率是1-y，列方程$$-3y+2(1-y)=2y+(-1)\ast (1-y)$$
解得y也等于$\frac{3}{8}$，而美女每次的期望收益则是 $2(1-y)-3y=\frac{1}{8}$ 元。这告诉我们，在双方都采取最优策略的情况下，平均每次美女赢$\frac{1}{8}$元。其实只要美女采取了$(\frac{3}{8},\frac{5}{8})$这个方案，不论你再采用什么方案，都是不能改变局面的。如果全部出正面，每次的期望收益是

$\frac{3+3+3-2-2-2-2-2}{8}=-\frac{1}{8}$元

如果全部出反面，每次的期望收益也是

$\frac{-2-2-2+1+1+1+1+1}{8}=-\frac{1}{8}$元。

而任何策略无非只是上面两种策略的线性组合，所以期望还是$-\frac{1}{8}$元。但是当你也采用最佳策略时，至少可以保证自己输得最少。否则，你肯定就会被美女采用的策略针对，从而赔掉更多。

总的来说“博弈论”其本质是将日常生活中的竞争矛盾以游戏的形式表现出来，并使用数学和逻辑学的方法来分析事物的运作规律。既然有游戏的参与者那么也必然存在游戏规则的制定者。深入的了解竞争行为的本质，有助于我们分析和掌握竞争中事物之间的关系，更方便我们对规则进行制定和调整，使其最终按照我们所预期的目的进行运作。

四大博弈模型

一、巴什博弈

定义：一堆$n$个物品，两个人轮流从中取出不多于$m$个，最后取光者胜，不能继续取的人输；

结论：若$n\%(m+1)!=0$，则先手必胜；反之，先手必输。

证明：若$n\%(m+1)!=0$，记 $n=k\ast (m+1)+r$，先者取走$r$个，那么设后者$t$个，只要先者拿$(m+1-t)$个，即始终和后者拿的数目之和为$(m+1)$,先手必胜。反之，先手必输。

二、尼姆博弈 ※

尼姆博弈是我们重点学习的一个模型。
定义：$n$堆物品，每堆物品的个数任意，两人轮流取，每次取某堆中不少于1个，最后取完者胜。

结论：将每堆物品的数量全部异或起来，若值为0，则先手必败，否则先手必胜。

证明： 证明可参考算法竞赛进阶指南 0X3A.

我们将每堆物品数异或起来为0这个状态称为必败态，顾名思义，这个状态下，谁取谁必败。因为当这个状态时，经过两人轮流取物，后者始终可以维持这个必败态，即A取完后，B一定可以取一个数，使得取完后每堆物品数异或起来仍为0。这样一直到最后一轮，B取完一定会使每堆数都为0，此时同样也是必败态（异或起来为0），这时B获胜，A面对所有堆都为0这个状态取，直接失败。

所以当每堆物品数全部异或起来，若值为0，此时已是必败态，先手必败；若值不为0，则先手一定会取一个数使得每堆数异或起来为0，达到必败态，从而后手必败。

注： 博弈时，每个人都会走当前最优策略，所以每个人都会尽量给对方创造必败态，给自己创造必胜态。

代码实现

	int r=0;
	for(int i=1;i<=n;++i)
	{
		r=r^a[i];
	} 
	if(r) return true;
	else return false;

SG函数

实际题目中，并不可能给出如此标准的博弈模型。对于更加一般的博弈论问题，我们需要通过SG函数转化为尼姆博弈的方式进行求解。关于SG函数在后面有更加详细的讲解。

三、斐波那契博弈

定义：有一堆物品，共$n$个，两人轮流取物，先手可取任意件，但不能不取，也不能把物品取完，之后每次取的物品数不能超过上一次的两倍，且至少为1件，取走最后一件物品的人获胜。

结论：当且仅当n不是斐波那契数时，先手胜。

证明：此博弈的证明需要各种不等式关系证明，一般记住结论即可，具体证明可以看 这篇文章

四、威佐夫博弈

定义：有两堆物品，数量分别为$a$个和$b$个，两人轮流取物，每次可以从一堆中取出任意个，也可以从两堆中取出相同数量的物品，每次至少要取一个，最后取完所有物品的人获胜。

结论：若$abs(a-b)\ast \frac{\sqrt{5}+1}{2}==min(a,b)$成立，则后手获胜，否则先手胜。其中$\frac{\sqrt{5}+1}{2}$为黄金分割比。

证明：这个证明比较神奇，也出现了神奇的黄金分割率，具体证明可以看 这篇文章

SG函数

首先给出一种 ICG（公平组合游戏）博弈游戏模型：给定一个有向无环图和一个起始顶点上的一枚棋子，两名选手交替的将这枚棋子沿有向边进行移动，无法移动者判负。

将ICG问题进行转换：任意一个ICG都可以通过把每个局面看成一个顶点，对每个局面和它的子局面连成一条有向边来抽象成这个有向图游戏。

首先定义一个mex函数，mex函数就是求集合中未出现的最小的非负整数。例如mex{0,1,2,4}=3，mex{2,3,5}=0，mex{}=0；

对于一个给定的有向无环图，定义关于图的每个顶点的SG函数SG如下(yi是x的后继) 。$$SG(x)=mex(SG(y1),SG(y2),\dots ,SG(yk))$$
特别地，整个有向图G的SG值被定义为有向图起点s的SG值即$SG(G)=SG(s)$。
下面我们借助图的形式来理解一下：

根据以下步骤建树：
一、找出必败态（SG值为0）
二、找出当前所有状态的前驱结点
三、根据定义计算结点的SG值
四、重复以上步骤，直到建树完成

操作如下：
Step 1：找出所有的必败态

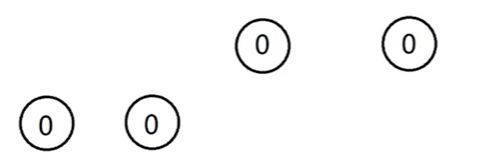
Step 2：寻找到能转移到必败态的结点，并加入到图中

Step 3：根据定义计算结点的SG值

Step 4：重复操作直到建树完成


这样我们就建树完成。

此时根结点SG值为0，我们可以知道这个点一定是必败态，这样是因为我们从这个点每个人交替进行移动，先手有两种选择，向左和向右。若向右移动，显然后手的人在移动一步就会到达先手的必败态，此时先手输。同理向左。

有向图游戏的和

设$G_1,G_2,...,G_m$是$m$个有向图游戏。定义有向图游戏$G$，它的行动规则是任选某个有向图游戏$G_i$，并在$G_i$上行动一步。$G$被称为有向图游戏$G_1,G_2,...,G_m$的和。

有向图游戏的和的SG函数值等于它所包含的各个子游戏SG值的异或和，即$$SG(G)=SG(G_1)xorSG(G_2)xor...SG(G_m)$$
而终点也就是游戏结束局面的$SG(x)=0$。

则有：
有向图游戏的某个局面必胜，当且仅当该局面对应节点的SG函数值大于0
有向图游戏的某个局面必败，当且仅当该局面对应节点的SG函数值等于0

证明请参考 这篇文章

深入学习SG函数

对于SG函数的进一步学习，请阅读 这篇文章 （推荐阅读）

例题

Luogu：

例题1

P4101 [HEOI2014]人人尽说江南好

例题1 题解 戳这里

例题2

P2594 [ZJOI2009]染色游戏

练习

Luogu：

练习1

P2197 【模板】nim游戏

练习2

P5675 [GZOI2017]取石子游戏

练习3

P3210 [HNOI2010]取石头游戏

参考文献

博弈论-百度百科
https://baike.baidu.com/item/%E5%8D%9A%E5%BC%88%E8%AE%BA/81545?fr=aladdin

博弈论总结 四大博弈模型 SG函数
https://blog.csdn.net/qq_45735851/article/details/108285065?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522161406683216780265466614%2522%252C%2522scm%2522%253A%252220140713.130102334.pc%255Fall.%2522%257D&request_id=161406683216780265466614&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2_allfirst_rank_v2~rank_v29-13-
108285065.first_rank_v2_pc_rank_v29&utm_term=%E5%8D%9A%E5%BC%88%E8%AE%BA

【ACM】博弈论基础
https://www.bilibili.com/video/BV15b411W73J?from=search&seid=3472685741901795478

算法竞赛进阶指南 李煜东
https://book.douban.com/subject/30136932/

写在后面： 博弈论的相关知识需要根据题目条件寻找最优的博弈策略，是一种思维上的跳跃（本人觉得和贪心差不多hh）