快速排序和归并排序非递归的详解
在经过主页中《八大排序》(下)的学习,我们了解了快速排序和归并排序且都是递归的思想,但是如果递归的深度很深呢?这一节我们就引出用非递归的思想解决这个问题。
快速排序非递归及归并排序非递归
- 快速排序非递归
-
- 思想
- 代码
- 快排非递归总结
- 归并排序非递归
-
- 思想
- 代码
- 归并非递归总结
- 总代码
-
- Stack.h
- Stack.c
- Sort.c
- 结语
快速排序非递归
大家都知道递归是在栈帧上建立空间(Windows默认1兆,Linux默认8兆),如果递归的深度太深,建立的栈帧过大呢?
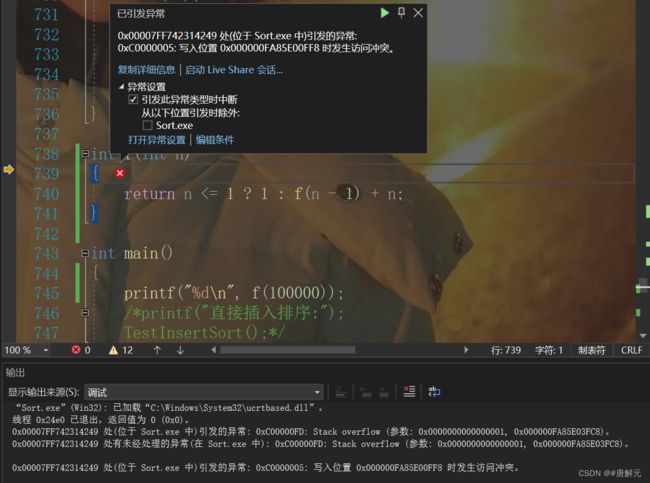
**递归的缺陷:**如果栈帧的深度太深,栈空间不够用,就会导致栈溢出。
思想
既然递归有一定的缺陷,那么我们怎么确定非递归的思路呢?
- 1.直接改循环(但是只能针对比较简单的);
- 2.借助数据结构的栈来模拟递归过程(针对复杂情况)。
针对快排我们就用第二种思路。第二种非递归思想中用到的栈是我们malloc出来的,是在堆上申请的,堆上的空间很大,和操作系统的栈并 不是一样的。
步骤:
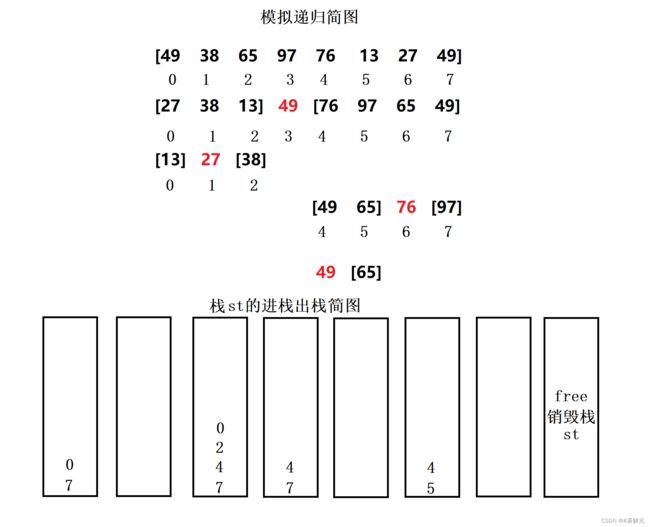
- 单趟和挖坑法一样,既然是模拟递归,那么和递归是很相似的
- 1.先在序列中选出一个基准值keyIndex,并将这个keyIndex放到相应地位置上,使左边比keyIndex小,右边比keyIndex大;
- 2.将整个区间划分三个区间:[left,keyIndex-1] keyIndex [keyIndex+1,right],由于栈是先进后出的原则,先把右区间压栈到下面,左区间压栈到上面;
- 3.如果左半区间内有多个数据,重复步骤1和步骤2,直到左半区间全部处理完了,再去处理右区间;
- 4.如果右半区间内有多个数据,重复步骤1和步骤2,当右半区间有序后,整个序列就就是有序的。
代码
void QuickSortNonR(int* a,int n)
{
ST st;
StackInit(&st);//初始化一个栈
StackPush(&st, n - 1);//把数组中最后一个元素入进去
StackPush(&st, 0);//把数组中第一个元素入进去
while (!StackEmpty(&st))
{
int left = StackTop(&st);//取栈顶数据
StackPop(&st);//出栈
int right = StackTop(&st);
StackPop(&st);
//单趟排选谁无所谓
int keyIndex = PartSort1(a, left, right);//这里单趟排序用的是挖坑法,前后指针和左右指针都可以。
//[left,keyIndex-1] keyIndex [keyIndex+1,right]此时数组被分为了三个区间
//入栈先入右区间,再入左区间,这样就可以先处理左区间,再处理右区间
if (keyIndex + 1 < right)//表示右区间内还有多个数据,无序就入栈
{
StackPush(&st, right);
StackPush(&st, keyIndex + 1);
}
if (left < keyIndex - 1)//表示左区间内还有多个数据,无序就入栈
{
StackPush(&st, keyIndex - 1);
StackPush(&st, left);
}
}
StackDestory(&st);
}
void TestQuickSort()
{
int a[] = { 49, 38, 65, 97, 76, 13, 27, 49 };
QuickSortNonR(a, sizeof(a) / sizeof(int));
PrintArray(a, sizeof(a) / sizeof(int));
}
快排非递归总结
快排非递归思想性能和递归思想两者性能几乎没有差距,但是非递归很好的解决了栈溢出问题。
归并排序非递归
思想
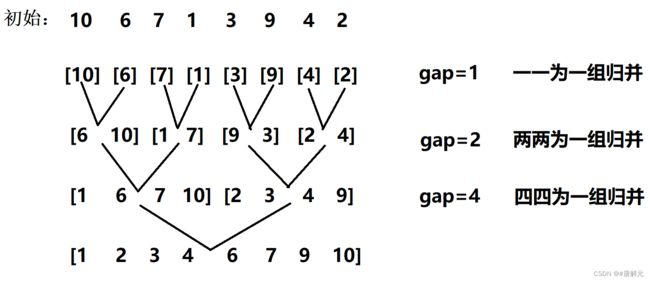
在上文中我们了解到递归改非递归有两种,一种是循环解决,另一种是用栈模拟递归
这里我们使用循环就完全可以了。归并排序递归思想和非递归思想恰恰相反,递归思想是将序列分解为不可再分的子序列再进行归并,而非递归是将序列直接以不可再分的子序列进行归并。如图:
代码
void MergeSortNonR(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
int gap = 1;//每组数据个数
while (gap < n)
{
for (int i = 0; i < n; i += 2 * gap)
{
//[i,i+gap-1] [i+gap,i+2*gap-1]
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
int index = i;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[index++] = a[begin1++];
}
else
{
tmp[index++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[index++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[index++] = a[begin2++];
}
//拷贝回去--把临时数组内的元素拷贝到原数组中
}
for (int j = 0; j < n; ++j)
{
a[j] = tmp[j];
}
gap *= 2;//刚才是11一组归并,*=2让2倍归并
}
free(tmp);
}
void TestMergeSort()
{
int a[] = { 10, 6, 7, 1, 3, 9, 4, 2 };
MergeSortNonR(a, sizeof(a) / sizeof(int));
PrintArray(a, sizeof(a) / sizeof(int));
}
int main()
{
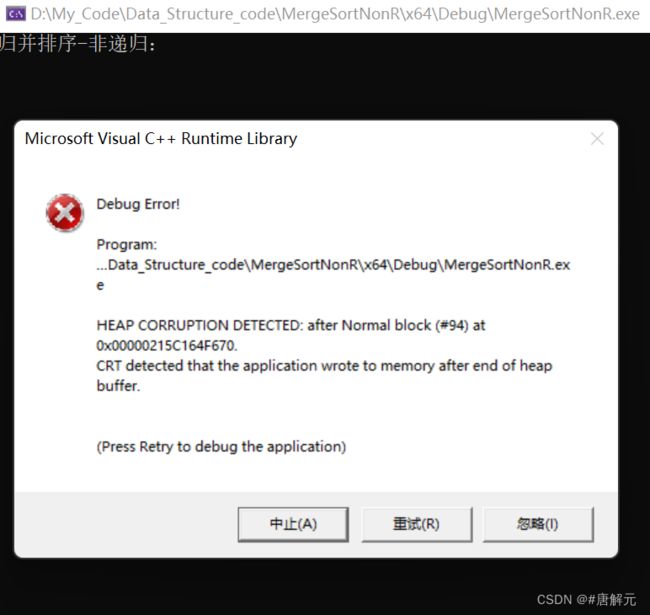
printf("归并排序-非递归:");
TestMergeSort();
return 0;
}
问题:
上面是我们理想的状态,就像满二叉树一样,数组长度不是2的整数次方的话,就会存在数组越界的情况,总结一下有以下三种情况:
- 1.归并过程中左区间存在,但是右半区间不存在;
- 2.归并过程中左区间存在,但是右半区间有且只有一部分;
- 3.归并过程中左半区间有且只有一部分,右半区间不存在。
问题处理:
对上面三个问题的解决:
- 1.那就不需要归并了
if (begin2 >= n) break;- 2.将end2修正一下
if (end2 >= n) { end2 = n - 1; }- 3.不对左半区间进行处理,将拷贝回去的代码放到for循环里,归并一部分拷贝一部分
for (int j = i; j <= end2; ++j) { a[j] = tmp[j]; }
//归并排序——非递归
//时间复杂度是O(N*logN)
void MergeSortNonR(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int)*n);
int gap = 1;//每组数据个数
while (gap < n)
{
for (int i = 0; i < n; i += 2*gap)
{
//[i,i+gap-1] [i+gap,i+2*gap-1]
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
//归并过程中右半区间可能不存在
if (begin2 >= n)
break;
//归并过程中右半区间有且不多(算多了)修正一下
if (end2 >= n)
{
end2 = n - 1;
}
int index = i;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[index++] = a[begin1++];
}
else
{
tmp[index++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[index++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[index++] = a[begin2++];
}
//拷贝回去--把临时数组内的元素拷贝到原数组中
for (int j = i; j <= end2; ++j)
{
a[j] = tmp[j];
}
}
gap *= 2;//刚才是11一组归并,*=2让2倍归并
}
free(tmp);
}
void TestMergeSort()
{
int a[] = { 10, 6, 7, 1, 3, 9, 4, 2 };
MergeSortNonR(a, sizeof(a) / sizeof(int));
PrintArray(a, sizeof(a) / sizeof(int));
}
归并非递归总结
时间复杂度还是不错的和归并排序递归是一样的都是O(N*logN)。
总代码
Stack.h
#include Stack.c
#include"Stack.h"
void StackInit(ST* ps)
{
assert(ps);
ps->a = (STDataType*)malloc(sizeof(STDataType) * 4);
if (ps->a == NULL)
{
printf("malloc fail\n");
exit(-1);
}
ps->capacity = 4;
ps->top = 0;
}
void StackDestory(ST* ps)
{
assert(ps);
free(ps->a);
ps->a = NULL;
ps->top = ps->capacity = 0;
}
void StackPush(ST* ps, STDataType x)
{
assert(ps);
//满了怎么办?---增容
if (ps->top == ps->capacity)
{
STDataType* tmp = (STDataType*)realloc(ps->a, ps->capacity * 2 * sizeof(STDataType));
if (tmp == NULL)
{
printf("realloc fail\n");
exit(-1);
}
else
{
ps->a = tmp;
ps->capacity *= 2;//乘等2才会变成它的二倍
}
}
ps->a[ps->top] = x;
ps->top++;
}
void StackPop(ST* ps)
{
assert(ps);
//栈空了,调用pop,直接中止程序并报错
assert(ps->top > 0);
ps->top--;
}
STDataType StackTop(ST* ps)
{
assert(ps);
//栈空了,调用top,直接中止程序并报错
assert(ps->top > 0);
return ps->a[ps->top - 1];
}
int StackSize(ST* ps)
{
assert(ps);
return ps->top;//top所在数组的下标就是栈的长度
}
bool StackEmpty(ST* ps)
{
assert(ps);
return ps->top == 0;//如果为空返回非零结果,如果不为空返回0
}
Sort.c
这里因为快速排序非递归中用到了单趟排序,所以直接在拷贝了一份挖坑法的单趟排序,不理解的可以去看《八大排序》(下)
#include"Stack.h"
void PrintArray(int* a, int n)
{
for (int i = 0; i < n; ++i)
{
printf("%d ", a[i]);
}
printf("\n");
}
//交换
void Swap(int* p1, int* p2)
{
int* tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
//三数取中--为了解决我们key选择的数不是最大,也不是最小的
int GetMidIndex(int* a, int left, int right)
{
int mid = (left + right) >> 1;
if (a[left] < a[mid])//如果左小于中间
{
if (a[mid] > a[right])//如果左小于中间,中间大于右,则返回中间
{
return mid;
}
else if (a[left] > a[right])//如果左小于中间,左大于右,则返回左
{
return left;
}
else
{
return right;//如果左小于中间,中间大于右,则返回右
}
}
else //a[left] > a[mid]
{
if (a[mid] > a[right])
{
return mid;
}
else if (a[left] < a[right])
{
return left;
}
else
{
return right;
}
}
}
int PartSort1(int* a, int left, int right)
{
int index = GetMidIndex(a, left, right);//三数取中
//Swap(&a[left], &a[index]);
int begin = left, end = right;
int pivot = begin;
int key = a[begin];
//单趟排序
//单趟排序时间复杂度是O(N)-begin从左向右走,end从右向左走
while (begin < end)
{
//右边找小,放到左边
while (begin < end && a[end] >= key)
--end;
//小的放到左边的坑里,自己形成新的坑位
a[pivot] = a[end];
pivot = end;
//右边找大
while (begin < end && a[begin] <= key)
++begin;
//大的放到右边的坑里,自己形成新的坑位
a[pivot] = a[begin];
pivot = begin;
}
//把小的放到pivot的左边,大的放到pivot的右边后,把key的值放到数组pivot的位置
pivot = begin;
a[pivot] = key;
//返回的是坑的位置
return pivot;
}
//快速排序--非递归
void QuickSortNonR(int* a, int n)
{
ST st;
StackInit(&st);//初始化一个栈
StackPush(&st, n - 1);//把数组中最后一个元素入进去
StackPush(&st, 0);//把数组中第一个元素入进去
while (!StackEmpty(&st))//当栈里没有区间的时候就结束
{
int left = StackTop(&st);
StackPop(&st);
int right = StackTop(&st);
StackPop(&st);
//单趟排选谁无所谓
int keyIndex = PartSort1(a, left, right);//这里单趟排序用的是挖坑法,前后指针和左右指针都可以。
//[left,keyIndex-1] keyIndex [keyIndex+1,right]此时数组被分为了三个区间
//入栈先入右区间,再入左区间,这样就可以先处理左区间,再处理右区间
if (keyIndex + 1 < right)//表示右区间内还有多个数据,无序就入栈
{
StackPush(&st, right);
StackPush(&st, keyIndex + 1);
}
if (left < keyIndex - 1)//表示左区间内还有多个数据,无序就入栈
{
StackPush(&st, keyIndex - 1);
StackPush(&st, left);
}
}
StackDestory(&st);//栈销毁
//非递归中malloc的空间是在操作系统的堆上面的,因为堆很大,所以空间并没有什么影响,
//malloc的空间是在操作系统上的,与数据结构的栈(栈和队列)和堆(二叉树)没有关系
}
void TestQuickSort()
{
int a[] = { 49, 38, 65, 97, 76, 13, 27, 49 };
QuickSortNonR(a, sizeof(a) / sizeof(int));
PrintArray(a, sizeof(a) / sizeof(int));
}
//归并排序——非递归
//时间复杂度是O(N*logN)
void MergeSortNonR(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
int gap = 1;//每组数据个数
while (gap < n)
{
for (int i = 0; i < n; i += 2 * gap)
{
//[i,i+gap-1] [i+gap,i+2*gap-1]
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
//归并过程中右半区间可能不存在
if (begin2 >= n)
break;
//归并过程中右半区间有且不多(算多了)修正一下
if (end2 >= n)
{
end2 = n - 1;
}
int index = i;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[index++] = a[begin1++];
}
else
{
tmp[index++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[index++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[index++] = a[begin2++];
}
//拷贝回去--把临时数组内的元素拷贝到原数组中
for (int j = i; j <= end2; ++j)
{
a[j] = tmp[j];
}
}
gap *= 2;//刚才是11一组归并,*=2让2倍归并
}
free(tmp);
}
void TestMergeSort()
{
int a[] = { 10, 6, 7, 1, 3, 9, 4, 2 };
MergeSortNonR(a, sizeof(a) / sizeof(int));
PrintArray(a, sizeof(a) / sizeof(int));
}
int main()
{
printf("快速排序-非递归:");
TestQuickSort();
printf("归并排序-非递归:");
TestMergeSort();
return 0;
}
结语
熬夜写的,写着写着脑子就不太灵光了,懵懵的文章中有错误欢迎大家积极指出哦