ai俄罗斯方块java_俄罗斯方块进阶--AI俄罗斯方块
原标题:俄罗斯方块进阶--AI俄罗斯方块
人工智能大火的今天,如果还是自己玩俄罗斯方块未免显得太LOW,为什么不对游戏升级,让机器自己去玩俄罗斯方块呢?有了这个想法之后利用周六周日两天的时间去搜集了大量的资料,在电脑死机好多次之后终于将AI俄罗斯方块实现了。
程序介绍
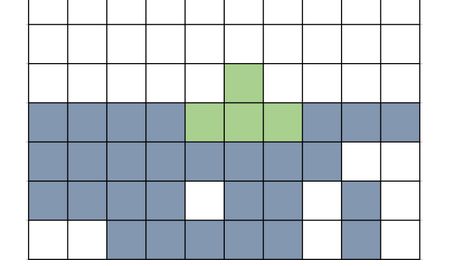
所谓让机器自己去玩俄罗斯方块,就是让机器计算当前方块的所有形态可放置的所有位置,然后根据统一的评价标准,计算出最优的位置进行放置。这个评价的标准简单的来说就是:板块放置的位置越靠下越好,方块之间越紧密越好,自身对消除行的方块贡献数量越多越好,但是这里还要注意的是不可为了追求消除行数,而去造成过多的空洞,这样也是不合理的。
关于AI算法主要有两种:一种是经典的Pierre Dellacherie算法,一种基于基于深度搜索的算法。深度搜索需要优化的地方很多,假如计算的层数不够、没有高效的剪枝,一不小心容易写成人工智障,时间复杂度也不好。Pierre Dellacherie算法更加清晰,复杂度更低。但是该算法只考虑当前,不对未来的情况进行计算,注重的是“不死性”,追求方块的“密集”,有时就算可以一次性消除 3 行,却会使全局方块更加“疏”,即过多的空洞。
代码由三部分组成Tetris.py,AI.py和Utils.py游戏的主要逻辑由Tetis控制,Utils定义了方块的样式,AI顾名思义实现了主要的AI算法。
具体介绍Pierre Dellacherie算法
只考虑当前方块,不对未来的情况进行计算,注重的是“不死性”,算法每次生成一个方块,便穷举该方块所有旋转的所有落点。一种方块最多有 4 种旋转,并且由于游戏界面是10*20的,所以对于每个旋转形状,只需要考虑10种落点。算法的核心是一个评估函数,对穷举出的每一种下落情况,计算 6 个参数值,用评估函数加权求和得到一个值,该值最大的情况便是目前方块的最优下落位置,六个参数分别是:
1.下落高度(Landing Height):
当前方块落下去之后,方块中点距底部的方格数事实上,不求中点也是可以的,详见官网。2.消行数(Rows eliminated)
消行层数与当前方块贡献出的方格数乘积3.行变换(Row Transitions):
从左到右(或者反过来)检测一行,当该行中某个方格从有方块到无方块(或无方块到有方块),
视为一次变换。游戏池边界算作有方块。行变换从一定程度上反映出一行的平整程度,越平整值越小
该指标为所有行的变换数之和
如图:■表示有方块,□表示空格(游戏池边界未画出)
■■□□■■□□■■□□ 变换数为6
□□□□□■□■□■□■ 变换数为9
■■■■□□□□□□■■ 变换数为2
■■■■■■■■■■■■ 变换数为04.列变换(Column Transitions):大意同上
列变换从一定程度上反映出一列中空洞的集中程度,空洞越集中值越小5.空洞数(Number of Holes)
不解释6.井的总和(Well Sums):
井指两边皆有方块的空列。该指标为所有井的深度连加到1再求总和注意一列中可能有多个井,如图:
■□□
■□■
■□■
■■■
■□■
■□■
■□■
中间一列为井,深度连加到一的和为 (2+1)+(3+2+1)=9
评估函数如下 (首字母简写):
关于方块形态
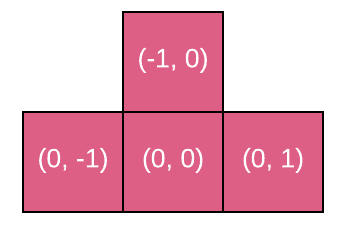
相对于上次文章中的俄罗斯方块,这里对AI俄罗斯方块的形态做一下特别说明,各个方块都是根据中心点的坐标来生成的,以(0,0)为中心点,在x、y轴加减1则是其他方格的坐标,这个好处就是只要确定中心点坐标,其他的方格位置就能随即生成。看图就懂↓
1# 每种块包含的四个小方块相对坐标分布
2self.shapes_relative_coords = [
3[[ 0, 0], [ 0, 0], [ 0, 0], [ 0, 0]],
4[[ 0, -1], [ 0, 0], [ 0, 1], [ 0, 2]],
5[[ 0, -1], [ 0, 0], [ 0, 1], [ 1, 1]],
6[[ 0, -1], [ 0, 0], [ 0, 1], [ -1, 1]],
7[[ 0, -1], [ 0, 0], [ 0, 1], [ 1, 0]],
8[[ 0, 0], [ 0, -1], [ 1, 0], [ 1, -1]],
9[[ 0, 0], [ 0, -1], [ -1, 0], [ 1, -1]],
10[[ 0, 0], [ 0, -1], [ 1, 0], [ -1, -1]]
11]
基于深度搜索
暂时不对此方法作介绍。
收获成果
责任编辑: