判断子序列

问题描述

给定字符串s和t,判断s是否为t的子序列?

解法1:双指针法

思路很简单,设计两个指针,分别用以遍历母字符串t和子字符串t.每一次遍历到子字符串的某个元素,开始遍历母字符串,直到母字符串也有相同的元素对应,这之后指向两个字符串的指针分别自增1.再进行如上判断.直到对于子串的某个元素母串没有对应的匹配或者子串遍历完毕为止.



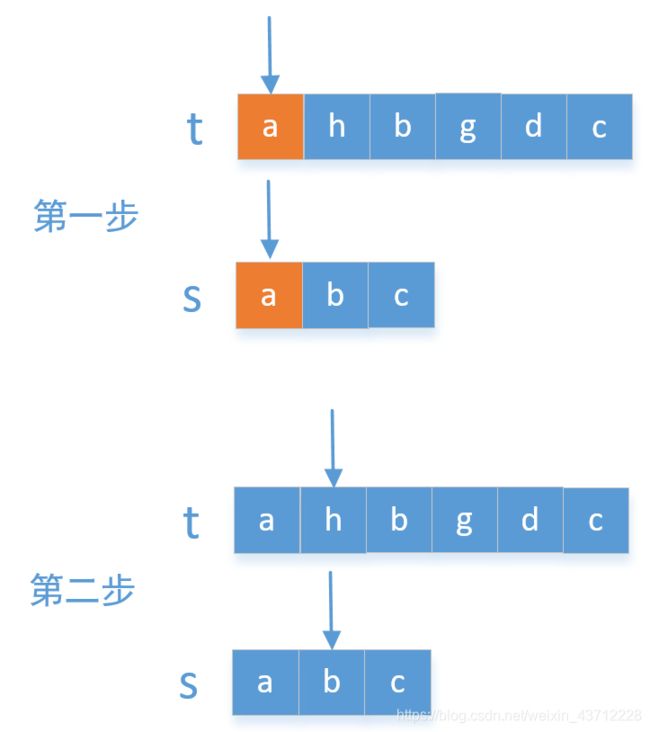
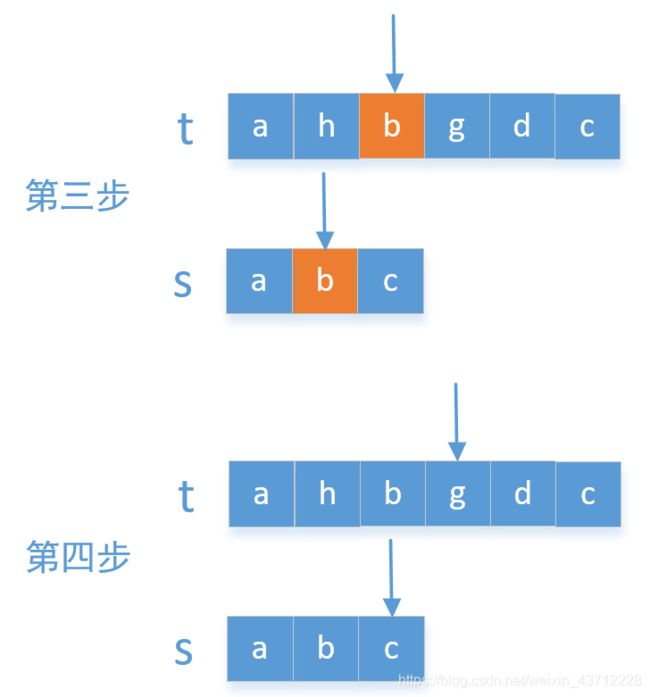
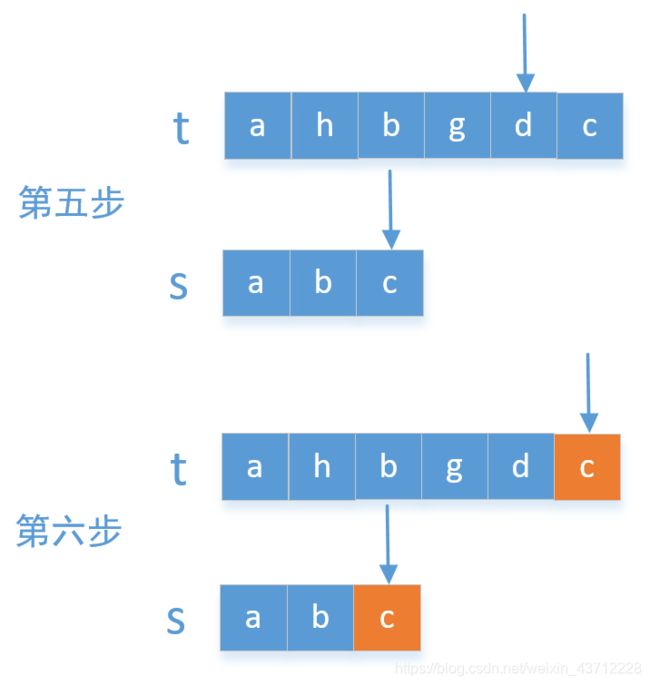
原理很简单,在此就不贴代码了(其实我也没写哈哈)

解法2.动态规划法

其实动态规划法特别适合求这种判断子串子序列的问题,之前的博客中曾经具体讨论过求两个字符串的公共子串和公共子序列的长度的问题.这里其实也差不多.我们用dp[i][j]来表示字符串t的前j个字符包含s的前i个字符,如果确实包含,则为true,否则为false.
它的递推公式是这样的:
1.如果s[i] == t[j],那么dp[i][j] = dp[i-1][j-1].也就是说,如果s的第i个元素等于t的第j个元素,那么t的前j个元素是否包含s的前i个元素本质上和t的前j-1个元素是否包含s的前i-1个元素这两个问题是等价的,这个可以参考我之前的一篇博客
一篇文章带你读懂什么是编辑距离

2.如果s[i] != t[j],说明t的第j个元素并不等于s的第i个元素,但是它也不一定就是false.因为当j>k>=i的时候很有可能t的前k个元素就已经实现了包含s的前i个元素了,所以dp[i][j] = dp[i-1][j],也就是判断t的前j个元素是否包含s的前i个元素等价于判断t的前j-1个元素是否包含s的前i个元素.
我们用j指向母串t,用i指向子串i也是有深意的.因为按照我们的习惯,总是逐行填满元素,也就是先遍历母串,固定子串的元素,这就类似于双指针法中固定一个子串元素,寻找母串中是否有元素与之相等.如果母串中的某个元素和子串中的某个元素相等,这只是dp[i][j] = true的必要条件,**因为子序列是有顺序的,这也就表示s中的所有元素在t中保持相同的顺序,**才能说明t中有s这个子序列,如果只找到两个元素相等,还要看这个相等的元素位于s的位置,如果是第一个,那自然是true.但如果不是第一个,那就需要看t中这个元素之前的元素是否包含s中这个元素之前的元素,也就是j指针不断的后退去寻找s中前面的元素的对应.这在动态规划中,就变成了查看它的前一行前一列是否为true.接下来就是确定边界条件了,根据上面的分析,我们得知,**s的第一个元素在t中存在是s中前两个元素是t中的子序列的前提,而s的第二个元素在t中存在也是s中前三个元素是t中的子序列的前提…,**所以我们只要分别写满第一行和第一列这也就是边界条件了.
代码如下:

public class JudgeIfSubString {
    public boolean isSubsequence(String s, String t){
        if(s.length() == 0){
            return true;
        }
        boolean[][] dp = new boolean[s.length() + 1][t.length() + 1];
        //边界条件
        for(int j = 0; j < t.length(); j++){
            dp[0][j] = true;
        }
        for(int i = 1; i < s.length(); i++){
            for(int j = 1; j <= t.length(); j++){
                //递推公式
                if(s.charAt(i-1) == t.charAt(j-1)){
                    dp[i][j] = dp[i-1][j-1];
                }else{
                    dp[i][j] = dp[i][j-1];
                }
            }
        }
        return dp[s.length()][t.length()];
    }
}

解法3:逐个查找

如果熟悉java语言的都知道,在java中String类有这样一个方法,public int indexOf(int ch, int fromIndex),它表示的是在字符串中是否存在一个字符ch,并且是从字符串的下标fromIndex开始查找的.我们要做的是在t中查找s中的每一个字符,如果没找到,则返回false.如果找到了,就从t的下一个位置继续开始查.

/*
* 利用Java中的函数indexOf(int ch, int fromIndex)
* 从fromIndex开始寻找字符ch是否包含在字符串中,如果存在返回ch第一次出现的位置.否则返回-1.
* 其实就是双指针法.
* */
public class JudgeIfSubString2 {
    public boolean isSubsequence(String s, String t) {
        int index = -1;
        for(char c : s.toCharArray()){
            index = t.indexOf(c, index+1);
            if(index == -1){
                return false;
            }
        }
        return true;
    }
}

虽然动态规划的思想的确有点绕,但是其实本质上不难,后面我会继续寻找相关题目的.