线段树详解java 线段树完整模版 题目实战
目录
- 线段树引入
- 线段树原理及实现
- 线段树的数据结构
- 线段树的建立
- 线段树的更新
- 线段树的查询
- 线段树完整模版
- 题目实战
-
- 力扣729.我的日程安排表 I
- 力扣731.我的日程安排表 II
-
- 法一
- 法二
- 力扣732.我的日程安排表 III
- 力扣307.区域和检索 - 数组可修改
-
- 法一
- 法二
- 力扣715.Range 模块
- 力扣699.掉落的方块
- 力扣2407. 最长递增子序列 II
线段树引入
线段树解决的是「区间和」的问题,且该「区间」会被修改
什么意思呢?举个简单的例子,对于 nums = [1, 2, 3, 4, 5]
如果我们需要多次求某些区间的和,是不是首先想到了利用「前缀和」。
但是如果 nums 会被修改呢?比如:
把第 i 个元素修改成 x
把第 i 个元素增加 x
把区间 [i, j] 内的元素都增加 x
此时,如果我们再使用「前缀和」,就没那么高效了。因为每一次更新,前缀和数组必须也随之更新,时间复杂度为 O(n)
既然「前缀和」在这种场景下没那么高效了,所以就有了今天要介绍的「线段树」
线段树原理及实现
上面提到过:线段树解决的是「区间和」的问题,且该「区间」会被修改
所以线段树主要实现两个方法:「求区间和」&&「修改区间」,且时间复杂度均为 O(logn)
始终记住一句话:线段树的每个节点代表一个区间
nums = [1, 2, 3, 4, 5] 对应的线段树如下所示:
从图中可以看到,每个节点代表一个区间,而节点的值就是该区间的和 (其实还可以根据题目问题,改变表示的含义!!)
数字之和「总数字之和 = 左区间数字之和 + 右区间数字之和」
最大公因数 (GCD)「总 GCD = gcd(左区间 GCD, 右区间 GCD)」
最大值「总最大值 = max(左区间最大值,右区间最大值)」
不符合区间加法的例子:
众数「只知道左右区间的众数,没法求总区间的众数」
01 序列的最长连续零「只知道左右区间的最长连续零,没法知道总的最长连续零」
根节点代表的区间是问题的总区间,如这个例子,问题的总区间就是数组的长度 [0, 4]
其实线段树是一棵近似的完全二叉树,该例子就是一棵完全二叉树,但是有些情况不是完全二叉树
所以对于给定的一个问题,如果该问题的范围是确定的,那么该问题的线段树也是确定的,因为建立线段树的过程就是不断把区间「平分」的过程,直到区间长度为 1
注意:下面的所有实现均基于求「区间和」以及对区间进行「加减」的更新操作
线段树的数据结构
我们可以使用数组来表示一棵线段树,假如根节点为 i,那么左孩子的节点就为 2 * i,右孩子的节点就为 2 * i + 1 (前提:i 从 1 开始,否则则是2 * i + 1和2 * i + 2)
我们也可以使用链表来表示一棵线段树,其节点的数据结构如下:
class Node {
// 左右孩子节点
Node left, right;
// 当前节点值
int val;
}
个人比较倾向使用链表,因为比较节约内存,下面的实现均基于链表
线段树的建立
如果题目中给了具体的区间范围,我们根据该范围建立线段树。比如力扣307.区域和检索 - 数组可修改
public void buildTree(Node node, int start, int end) {
// 到达叶子节点
if (start == end) {
node.val = arr[start];
return ;
}
int mid = (start + end) >> 1;
node.left = new Node();
node.right = new Node();
buildTree(node.left, start, mid);
buildTree(node.right, mid + 1, end);
// 向上更新
pushUp(node);
}
// 向上更新
private void pushUp(Node node) {
node.val = node.left.val + node.right.val;
}
但是很多时候,题目中都没有给出很具体的范围,只有数据的取值范围,一般都很大,所以我们更常用的是「动态开点」
下面我们手动模拟一下「动态开点」的过程。同样的,也是基于上面的例子 nums = [1, 2, 3, 4, 5]
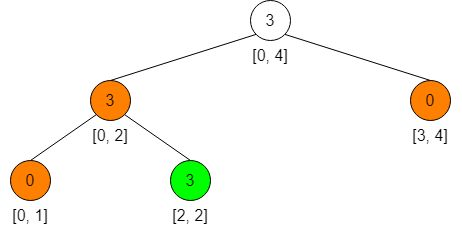
假设一种情况,最开始只知道数组的长度 5,而不知道数组内每个元素的大小,元素都是后面添加进去的。所以线段树的初始状态如下图所示
假设此时,我们添加了一个元素 [2, 2]; val = 3。现在线段树的结构如下图所示:
这里需要解释一下,如果一个节点没有左右孩子,会一下子把左右孩子节点都给创建出来,如上图橙色节点所示,具体代码可见下面介绍的方法 pushDown()
两个橙色的叶子节点仅仅只是被创建出来了,并无实际的值,均为 0;而另外一个橙色的非叶子节点,值为 3 的原因是下面的孩子节点的值向上更新得到的
下面给出依次添加剩余节点的过程:(注意观察值的变化!!)
「动态开点」一般是在「更新」或「查询」的时候动态的建立节点,具体可见下面的更新和查询操作
线段树的更新
大多数教程都是把更新分为两种:「点更新」和「区间更新」。其实这两种可以合并成一种,「点更新」不就是更新长度为 1 的区间嘛!
更新区间的前提是找到需要更新的区间,所以和查询的思路很相似
如果我们要把区间 [2, 4] 内的元素都「➕1」
我们会发现一个很有意思的现象,我们只把 [2,2] 和 [3,4] 这两个区间对应的节点更新了,而区间 [3, 3] 和 [4,4] 并没有更新
按道理来说,[3, 3] 和 [4,4] 也是需要更新的,不然当我们查询区间 [3, 3] 和 [4,4] 的值,就会出现错误!
这是因为我们使用了**「懒惰标记」**的方法,我们只需要更新到满足条件的区间即可,然后再给该区间对应的节点加一个懒惰标记,表示该节点所有对应的孩子节点都应该有此更新
当我们向孩子节点遍历的时候会把「懒惰标记」下推给孩子节点
我们需要稍微修改一下 Node 的数据结构
class Node {
// 左右孩子节点
Node left, right;
// 当前节点值
int val;
// 懒惰标记
int add;
}
基于「动态开点」的前提,我们下推懒惰标记的时候,如果节点不存在左右孩子节点,那么我们就创建左右孩子节点,先来实现下推懒惰标记的函数:
// leftNum 和 rightNum 表示左右孩子区间的叶子节点数量
// 因为如果是「加减」更新操作的话,需要用懒惰标记的值✖️叶子节点的数量
private void pushDown(Node node, int leftNum, int rightNum) {
// 动态开点
if (node.left == null) node.left = new Node();
if (node.right == null) node.right = new Node();
// 如果 add 为 0,表示没有标记
if (node.add == 0) return ;
// 注意:当前节点加上标记值✖️该子树所有叶子节点的数量
node.left.val += node.add * leftNum;
node.right.val += node.add * rightNum;
// 把标记下推给孩子节点
// 对区间进行「加减」的更新操作,下推懒惰标记时需要累加起来,不能直接覆盖!
node.left.add += node.add;
node.right.add += node.add;
// 取消当前节点标记
node.add = 0;
}
下面来实现更新的函数:
// 在区间 [start, end] 中更新区间 [l, r] 的值,将区间 [l, r] ➕ val
// 对于上面的例子,应该这样调用该函数:update(root, 0, 4, 2, 4, 1)
public void update(Node node, int start, int end, int l, int r, int val) {
// 找到了满足要求的区间
if (l <= start && end <= r) {//此时整个区间都要加 那就很方便了
// 区间节点加上更新值
// 注意:需要✖️该子树所有叶子节点
node.val += (end - start + 1) * val;
// 添加懒惰标记
// 对区间进行「加减」的更新操作,懒惰标记需要累加,不能直接覆盖
node.add += val;
return ;
}
int mid = (start + end) >> 1;
// 下推标记
// mid - start + 1:表示左孩子区间叶子节点数量
// end - mid:表示右孩子区间叶子节点数量
pushDown(node, mid - start + 1, end - mid);
// [start, mid] 和 [l, r] 可能有交集,遍历左孩子区间
if (l <= mid) update(node.left, start, mid, l, r, val);
// [mid + 1, end] 和 [l, r] 可能有交集,遍历右孩子区间
if (r > mid) update(node.right, mid + 1, end, l, r, val);
// 向上更新
pushUp(node);
}
线段树的查询
如果我们要查询区间 [2, 4] 的结果,如下图红色标记所示:
下面给出代码实现:
// 在区间 [start, end] 中查询区间 [l, r] 的结果,即 [l ,r] 保持不变
// 对于上面的例子,应该这样调用该函数:query(root, 0, 4, 2, 4)
public int query(Node node, int start, int end, int l, int r) {
// 区间 [l ,r] 完全包含区间 [start, end]
// 例如:[2, 4] = [2, 2] + [3, 4],当 [start, end] = [2, 2] 或者 [start, end] = [3, 4],直接返回
if (l <= start && end <= r) return node.val;
// 把当前区间 [start, end] 均分得到左右孩子的区间范围
// node 左孩子区间 [start, mid]
// node 左孩子区间 [mid + 1, end]
int mid = (start + end) >> 1, ans = 0;
// 下推标记
pushDown(node, mid - start + 1, end - mid);
// [start, mid] 和 [l, r] 可能有交集,遍历左孩子区间
if (l <= mid) ans += query(node.left, start, mid, l, r);
// [mid + 1, end] 和 [l, r] 可能有交集,遍历右孩子区间
if (r > mid) ans += query(node.right, mid + 1, end, l, r);
// ans 把左右子树的结果都累加起来了,与树的后续遍历同理
return ans;
}
线段树完整模版
注意:下面模版基于求「区间和」以及对区间进行「加减」的更新操作,且为「动态开点」
public class SegmentTreeDynamic {
class Node {
Node left, right;
int val, add;
}
private int N = (int) 1e9;//线段树范围大小
private Node root = new Node();
// 在区间 [start, end] 中更新区间 [l, r] 的值,将区间 [l, r] ➕ val
// 如果结点表示为「区间最值」的情况时在更新结点时不需要✖️叶子节点的数量
// 下面的pushDown函数里也是 也要根据题目判断是否需要✖️叶子节点的数量
// 如果是「点更新」 也不需要✖️叶子节点的数量 因为此时区间是一个点所以一定会更新到叶子节点
//start, end一般是用0和N 对应root的范围!
public void update(Node node, int start, int end, int l, int r, int val) {
if (l <= start && end <= r) {
node.val += (end - start + 1) * val;//✖️叶子节点的数量
node.add += val;//这里俩个+=如果在点赋值时可以改成= 点累加不行
return ;
}
int mid = (start + end) >> 1;
pushDown(node, mid - start + 1, end - mid);
if (l <= mid) update(node.left, start, mid, l, r, val);
if (r > mid) update(node.right, mid + 1, end, l, r, val);
pushUp(node);
}
// 在区间 [start, end] 中查询区间 [l, r] 的结果, [l ,r] 保持不变
public int query(Node node, int start, int end, int l, int r) {
if (l <= start && end <= r) return node.val;
int mid = (start + end) >> 1, ans = 0;
pushDown(node, mid - start + 1, end - mid);
if (l <= mid) ans += query(node.left, start, mid, l, r);
if (r > mid) ans += query(node.right, mid + 1, end, l, r);
return ans;
}
// 向上更新
private void pushUp(Node node) {
node.val = node.left.val + node.right.val;
}
// 推懒惰标记的函数
// 如果是「覆盖」的更新操作 则在下推懒惰标记的时候『不需要累加』
private void pushDown(Node node, int leftNum, int rightNum) {
if (node.left == null) node.left = new Node();
if (node.right == null) node.right = new Node();
if (node.add == 0) return ;
// 当前节点加上标记值✖️该子树所有叶子节点的数量 同上面update函数同步修改
node.left.val += node.add * leftNum;
node.right.val += node.add * rightNum;//这里俩个+=如果在点赋值时可以改成= 点累加不行
// 对区间进行「加减」的更新操作时,下推懒惰标记时需要累加起来,不能直接覆盖
node.left.add += node.add;
node.right.add += node.add;
node.add = 0;
}
}
再次强调一遍:上面给出的模版基于求「区间和」以及对区间进行「加减」的更新操作,且为「动态开点」
但是下面给出的题目实战中,有些题目需要对模版进行小小的修改,这里统一整理汇总一下
1.对于表示为「区间和」且对区间进行「加减」的更新操作的情况,我们在更新节点值的时候『需要✖️左右孩子区间叶子节点的数量 (注意是叶子节点的数量)』;我们在下推懒惰标记的时候『需要累加』!!(这种情况和模版一致!!)
如力扣933.最近的请求次数
2.对于表示为「区间和」且对区间进行「覆盖」的更新操作的情况,我们在更新节点值的时候『需要✖️左右孩子区间叶子节点的数量 (注意是叶子节点的数量)』;我们在下推懒惰标记的时候『不需要累加』!!(因为是覆盖操作!!)
如力扣307.区域和检索 - 数组可修改
3.对于表示为「区间最值」且对区间进行「加减」的更新操作的情况,我们在更新节点值的时候『不需要✖️左右孩子区间叶子节点的数量 (注意是叶子节点的数量)』;我们在下推懒惰标记的时候『需要累加』!!
如力扣729.我的日程安排表 I、力扣732.我的日程安排表 III
注意:对于题目 力扣933.最近的请求次数 和 区域和 力扣307.区域和检索 - 数组可修改 可以「不用✖️左右孩子区间叶子节点的数量」
为什么??因为这两个题目是「点更新」,在介绍线段树更新的时候,我们说过:「点更新」和「区间更新」可以合并成一种,「点更新」不就是更新长度为 1 的区间嘛!!
上面两个题目调用更新函数的方式为:update(root, 1, N, t, t, 1); 和 update(root, 0, N, i, i, nums[i]);
由于区间是一个点,所以一定会更新到叶子节点,故可以不用✖️左右孩子区间叶子节点的数量!!
题目实战
力扣729.我的日程安排表 I
题目
class MyCalendar {
public MyCalendar() {
}
public boolean book(int start, int end) {
// 先查询该区间是否为 0
if (query(root, 0, N, start, end - 1) != 0) return false;
// 更新该区间
update(root, 0, N, start, end - 1, 1);
return true;
}
// *************** 下面是模版 ***************
class Node {
// 左右孩子节点
Node left, right;
// 当前节点值,以及懒惰标记的值
int val, add;
}
private int N = (int) 1e9;
private Node root = new Node();
public void update(Node node, int start, int end, int l, int r, int val) {
if (l <= start && end <= r) {
node.val += val;
node.add += val;
return ;
}
pushDown(node);
int mid = (start + end) >> 1;
if (l <= mid) update(node.left, start, mid, l, r, val);
if (r > mid) update(node.right, mid + 1, end, l, r, val);
pushUp(node);
}
public int query(Node node, int start, int end, int l, int r) {
if (l <= start && end <= r) return node.val;
pushDown(node);
int mid = (start + end) >> 1, ans = 0;
if (l <= mid) ans = query(node.left, start, mid, l, r);
if (r > mid) ans = Math.max(ans, query(node.right, mid + 1, end, l, r));
return ans;
}
private void pushUp(Node node) {
// 每个节点存的是当前区间的最大值
node.val = Math.max(node.left.val, node.right.val);
}
private void pushDown(Node node) {
if (node.left == null) node.left = new Node();
if (node.right == null) node.right = new Node();
if (node.add == 0) return ;
node.left.val += node.add;
node.right.val += node.add;
node.left.add += node.add;
node.right.add += node.add;
node.add = 0;
}
}
力扣731.我的日程安排表 II
题目
法一
套模板即可
class MyCalendarTwo {
// 让线段树结点保存区间最大值 值1表示预定了一次 2表示预定了2次
// 同时修改线段树query函数 让其返回区间最大值
public MyCalendarTwo() {
}
public boolean book(int start, int end) {
if(query(root,0,N,start,end-1)>1) return false;
else{
update(root,0,N,start,end-1,1);
return true;
}
}
class Node {
Node left, right;
int val, add;
}
private int N = (int) 1e9;//线段树范围大小
private Node root = new Node();
// 在区间 [start, end] 中更新区间 [l, r] 的值,将区间 [l, r] ➕ val
// 如果结点表示为「区间最值」的情况时在更新结点时不需要✖️叶子节点的数量
// 下面的pushDown函数里也是 也要根据题目判断是否需要✖️叶子节点的数量
// 如果是「点更新」 也不需要✖️叶子节点的数量 因为此时区间是一个点所以一定会更新到叶子节点
public void update(Node node, int start, int end, int l, int r, int val) {
if (l <= start && end <= r) {
node.val += val;//✖️叶子节点的数量
node.add += val;//这里俩个+=如果在点赋值时可以改成= 点累加不行
return ;
}
int mid = (start + end) >> 1;
pushDown(node, mid - start + 1, end - mid);
if (l <= mid) update(node.left, start, mid, l, r, val);
if (r > mid) update(node.right, mid + 1, end, l, r, val);
pushUp(node);
}
// 在区间 [start, end] 中查询区间 [l, r] 的最大值, [l ,r] 保持不变
public int query(Node node, int start, int end, int l, int r) {
if (l <= start && end <= r) return node.val;
int mid = (start + end) >> 1, ans = 0;
pushDown(node, mid - start + 1, end - mid);
if (l <= mid) ans = Math.max(ans,query(node.left, start, mid, l, r));
if (r > mid) ans = Math.max(ans,query(node.right, mid + 1, end, l, r));
return ans;
}
// 向上更新
private void pushUp(Node node) {
node.val = Math.max(node.left.val , node.right.val);
}
// 推懒惰标记的函数
// 如果是「覆盖」的更新操作 则在下推懒惰标记的时候『不需要累加』
private void pushDown(Node node, int leftNum, int rightNum) {
if (node.left == null) node.left = new Node();
if (node.right == null) node.right = new Node();
if (node.add == 0) return ;
// 当前节点加上标记值✖️该子树所有叶子节点的数量 同上面update函数同步修改
node.left.val += node.add;
node.right.val += node.add;//这里俩个+=如果在点赋值时可以改成= 点累加不行
// 对区间进行「加减」的更新操作时,下推懒惰标记时需要累加起来,不能直接覆盖
node.left.add += node.add;
node.right.add += node.add;
node.add = 0;
}
}
法二
官解提供的一种线段树解法,相较于上面的法一比较费时,也是一种建立线段树的思路,代码比较简洁。
class MyCalendarTwo {
Map<Integer, int[]> tree;//一种线段树表示方法 前面的int表示数组索引 后面的int[]来表示结点的存储值
//第一个值保存当前区间最大值 第二个值是该区间的懒标记(节省时间,更新结点时不需要更新到子节点)
//这里用1作为起始索引 那么左子树可认为是2i 右子树是2i+1
public MyCalendarTwo() {
tree = new HashMap<Integer, int[]>();
}
public boolean book(int start, int end) {
update(start, end - 1, 1, 0, 1000000000, 1);//从根结点进入 希望在[start, end - 1]进行+1操作
//tree.putIfAbsent(1, new int[2]); //官解这句话不知道有什么作用 删了也能过
if (tree.get(1)[0] > 2) {//已经满了 会产生三重预定
update(start, end - 1, -1, 0, 1000000000, 1);//从根结点进入 希望在[start, end - 1]进行-1操作
return false;
}
return true;
}
public void update(int start, int end, int val, int l, int r, int idx) {
if (r < start || end < l) {
return;
}
tree.putIfAbsent(idx, new int[2]);
if (start <= l && r <= end) {
tree.get(idx)[0] += val;
tree.get(idx)[1] += val;
} else {
int mid = (l + r) >> 1;
update(start, end, val, l, mid, 2 * idx);
update(start, end, val, mid + 1, r, 2 * idx + 1);
tree.putIfAbsent(2 * idx, new int[2]);
tree.putIfAbsent(2 * idx + 1, new int[2]);
tree.get(idx)[0] = tree.get(idx)[1] + Math.max(tree.get(2 * idx)[0], tree.get(2 * idx + 1)[0]);
}
}
}
力扣732.我的日程安排表 III
题目
套区间最值,区间加减模版即可。
class MyCalendarThree {
public MyCalendarThree() {
}
public int book(int startTime, int endTime) {
update(root,0,N,startTime,endTime-1,1);
return query(root,0,N,0,N);
}
class Node {
Node left, right;
int val, add;
}
private int N = (int) 1e9;//线段树范围大小
private Node root = new Node();
// 在区间 [start, end] 中更新区间 [l, r] 的值,将区间 [l, r] ➕ val
// 如果结点表示为「区间最值」的情况时在更新结点时不需要✖️叶子节点的数量
// 下面的pushDown函数里也是 也要根据题目判断是否需要✖️叶子节点的数量
// 如果是「点更新」 也不需要✖️叶子节点的数量 因为此时区间是一个点所以一定会更新到叶子节点
//这里是区间最值的区间更新 结点保存区间最大值
public void update(Node node, int start, int end, int l, int r, int val) {
if (l <= start && end <= r) {
node.val += val;
node.add += val;//这里俩个+=如果在点赋值时可以改成= 点累加不行
return ;
}
int mid = (start + end) >> 1;
pushDown(node, mid - start + 1, end - mid);
if (l <= mid) update(node.left, start, mid, l, r, val);
if (r > mid) update(node.right, mid + 1, end, l, r, val);
pushUp(node);
}
// 在区间 [start, end] 中查询区间 [l, r] 的结果, [l ,r] 保持不变
public int query(Node node, int start, int end, int l, int r) {
if (l <= start && end <= r) return node.val;
int mid = (start + end) >> 1, ans = 0;
pushDown(node, mid - start + 1, end - mid);
if (l <= mid) ans = query(node.left, start, mid, l, r);
if (r > mid) ans = Math.max(ans,query(node.right, mid + 1, end, l, r));
return ans;
}
// 向上更新 维护最大值
private void pushUp(Node node) {
node.val = Math.max(node.left.val , node.right.val);
}
// 推懒惰标记的函数
// 如果是「覆盖」的更新操作 则在下推懒惰标记的时候『不需要累加』
private void pushDown(Node node, int leftNum, int rightNum) {
if (node.left == null) node.left = new Node();
if (node.right == null) node.right = new Node();
if (node.add == 0) return ;
// 当前节点加上标记值✖️该子树所有叶子节点的数量 同上面update函数同步修改
node.left.val += node.add;
node.right.val += node.add;//这里俩个+=如果在点赋值时可以改成= 点累加不行
// 对区间进行「加减」的更新操作时,下推懒惰标记时需要累加起来,不能直接覆盖
node.left.add += node.add;
node.right.add += node.add;
node.add = 0;
}
}
力扣307.区域和检索 - 数组可修改
题目
法一
使用基于动态开点的方法,完全是为了加深对动态开点的理解,因为题目给定了数组大小且使用过程中不会改变数组大小,所以可以其实上来创建固定大小的线段树。
class NumArray {
public NumArray(int[] nums) {
N=nums.length-1;
for (int i = 0; i <= N; i++) {
updateTree(root,0,N,i,i,nums[i]);
}
}
public void update(int index, int val) {
updateTree(root,0,N,index,index,val);
}
public int sumRange(int left, int right) {
return query(root,0,N,left,right);
}
/*******下面为线段树模版********* */
class Node {
Node left, right;
int val, add;
}
private int N;//线段树范围大小
private Node root = new Node();
// 在区间 [start, end] 中更新区间 [l, r] 的值,将区间 [l, r] ➕ val
// 如果结点表示为「区间最值」的情况时在更新结点时不需要✖️叶子节点的数量
// 下面的pushDown函数里也是 也要根据题目判断是否需要✖️叶子节点的数量
public void updateTree(Node node, int start, int end, int l, int r, int val) {
if (l <= start && end <= r) {
node.val = val;//✖️叶子节点的数量
node.add = val;
return ;
}
int mid = (start + end) >> 1;
pushDown(node, mid - start + 1, end - mid);
if (l <= mid) updateTree(node.left, start, mid, l, r, val);
if (r > mid) updateTree(node.right, mid + 1, end, l, r, val);
pushUp(node);
}
// 在区间 [start, end] 中查询区间 [l, r] 的结果, [l ,r] 保持不变
public int query(Node node, int start, int end, int l, int r) {
if (l <= start && end <= r) return node.val;
int mid = (start + end) >> 1, ans = 0;
pushDown(node, mid - start + 1, end - mid);
if (l <= mid) ans += query(node.left, start, mid, l, r);
if (r > mid) ans += query(node.right, mid + 1, end, l, r);
return ans;
}
// 向上更新
private void pushUp(Node node) {
node.val = node.left.val + node.right.val;
}
// 推懒惰标记的函数
// 如果是「覆盖」的更新操作 则在下推懒惰标记的时候『不需要累加』
private void pushDown(Node node, int leftNum, int rightNum) {
if (node.left == null) node.left = new Node();
if (node.right == null) node.right = new Node();
if (node.add == 0) return ;
// 当前节点加上标记值✖️该子树所有叶子节点的数量 同上面updateTree函数同步修改
node.left.val = node.add;
node.right.val = node.add;
// 对区间进行「加减」的更新操作时,下推懒惰标记时需要累加起来,不能直接覆盖
node.left.add = node.add;
node.right.add = node.add;
node.add = 0;
}
}
法二
根据给定范围建树版本
class NumArray {
public NumArray(int[] nums) {
N=nums.length-1;
buildTree(root,0,N,nums);
}
public void update(int index, int val) {
updateTree(root,0,N,index,index,val);
}
public int sumRange(int left, int right) {
return query(root,0,N,left,right);
}
/*******下面为线段树模版********* */
class Node {
Node left, right;
int val, add;
}
private int N;//线段树范围大小
private Node root = new Node();
public void buildTree(Node node, int start, int end, int[] nums) {
// 到达叶子节点
if (start == end) {
node.val = nums[start];
return ;
}
int mid = (start + end) >> 1;
node.left = new Node();
node.right = new Node();
buildTree(node.left, start, mid, nums);
buildTree(node.right, mid + 1, end, nums);
// 向上更新
pushUp(node);
}
// 在区间 [start, end] 中更新区间 [l, r] 的值,将区间 [l, r] ➕ val
// 如果结点表示为「区间最值」的情况时在更新结点时不需要✖️叶子节点的数量
// 下面的pushDown函数里也是 也要根据题目判断是否需要✖️叶子节点的数量
public void updateTree(Node node, int start, int end, int l, int r, int val) {
if (l <= start && end <= r) {
node.val = val;//✖️叶子节点的数量
node.add = val;
return ;
}
int mid = (start + end) >> 1;
pushDown(node, mid - start + 1, end - mid);
if (l <= mid) updateTree(node.left, start, mid, l, r, val);
if (r > mid) updateTree(node.right, mid + 1, end, l, r, val);
pushUp(node);
}
// 在区间 [start, end] 中查询区间 [l, r] 的结果, [l ,r] 保持不变
public int query(Node node, int start, int end, int l, int r) {
if (l <= start && end <= r) return node.val;
int mid = (start + end) >> 1, ans = 0;
pushDown(node, mid - start + 1, end - mid);
if (l <= mid) ans += query(node.left, start, mid, l, r);
if (r > mid) ans += query(node.right, mid + 1, end, l, r);
return ans;
}
// 向上更新
private void pushUp(Node node) {
node.val = node.left.val + node.right.val;
}
// 推懒惰标记的函数
// 如果是「覆盖」的更新操作 则在下推懒惰标记的时候『不需要累加』
private void pushDown(Node node, int leftNum, int rightNum) {
if (node.add == 0) return ;
// 当前节点加上标记值✖️该子树所有叶子节点的数量 同上面updateTree函数同步修改
node.left.val = node.add;
node.right.val = node.add;
// 对区间进行「加减」的更新操作时,下推懒惰标记时需要累加起来,不能直接覆盖
node.left.add = node.add;
node.right.add = node.add;
node.add = 0;
}
}
力扣715.Range 模块
题目
class RangeModule {
public RangeModule() {
}
public void addRange(int left, int right) {//+1代表跟踪
update(root,1,N,left,right-1,1);
}
public boolean queryRange(int left, int right) {
return query(root,1,N,left,right-1)==1?true:false;
}
public void removeRange(int left, int right) {//-1代表取消跟踪
update(root,1,N,left,right-1,-1);
}
class Node {
Node left, right;
int val, add;//val表示当前区域是否被跟踪 1表示被跟踪 -1表示未被跟踪
}
private int N = (int) 1e9;//线段树范围大小
private Node root = new Node();
// 在区间 [start, end] 中更新区间 [l, r] 的值,将区间 [l, r] ➕ val
// 如果结点表示为「区间最值」的情况时在更新结点时不需要✖️叶子节点的数量
// 下面的pushDown函数里也是 也要根据题目判断是否需要✖️叶子节点的数量
// 如果是「点更新」 也不需要✖️叶子节点的数量 因为此时区间是一个点所以一定会更新到叶子节点
// 本题结点应该表示该区域是否被跟踪 可以理解为区间最值的一种 可以用区间最小值 1代表这个区间所有实数都被跟踪了
public void update(Node node, int start, int end, int l, int r, int val) {
if (l <= start && end <= r) {
if(val==-1){
node.val = -1;
node.add = -1;
}
else{//val=1
node.val = 1;
node.add = 1;
}
return ;
}
int mid = (start + end) >> 1;
pushDown(node, mid - start + 1, end - mid);
if (l <= mid) update(node.left, start, mid, l, r, val);
if (r > mid) update(node.right, mid + 1, end, l, r, val);
pushUp(node);
}
// 在区间 [start, end] 中查询区间 [l, r] 的结果, [l ,r] 保持不变
public int query(Node node, int start, int end, int l, int r) {
if (l <= start && end <= r) return node.val;
int mid = (start + end) >> 1, ans=1;
pushDown(node, mid - start + 1, end - mid);
if (l <= mid) ans = Math.min(ans,query(node.left, start, mid, l, r));
if (r > mid) ans = Math.min(ans,query(node.right, mid + 1, end, l, r));
return ans;
}
// 向上更新
private void pushUp(Node node) {
node.val = Math.min(node.left.val , node.right.val);
}
// 推懒惰标记的函数
// 如果是「覆盖」的更新操作 则在下推懒惰标记的时候『不需要累加』
private void pushDown(Node node, int leftNum, int rightNum) {
if (node.left == null) node.left = new Node();
if (node.right == null) node.right = new Node();
if (node.add == 0) return ;
// 当前节点加上标记值✖️该子树所有叶子节点的数量 同上面update函数同步修改
node.left.val = node.add;
node.right.val = node.add;
// 对区间进行「加减」的更新操作时,下推懒惰标记时需要累加起来,不能直接覆盖
node.left.add = node.add;
node.right.add = node.add;
node.add = 0;
}
}
力扣699.掉落的方块
题目
class Solution {
public List<Integer> fallingSquares(int[][] positions) {
List<Integer>list=new ArrayList<>();
int maxheight=0;
for (int[] position : positions) {
int height=query(root,1,N,position[0],position[0]+position[1]-1);//这里有个易错点的细节 就是区间右边界要-1
update(root,1,N,position[0],position[0]+position[1]-1,height+position[1]);//比如[[1,2]] 那么x轴上只有坐标1和2的高度是2 端点3的坐标还是0 你不能将另一个正方形放在它的端点上
maxheight=Math.max(maxheight,height+position[1]);
list.add(maxheight);
}
return list;
}
class Node {
Node left, right;
int val, add;
}
private int N = (int) 1e8;//线段树范围大小
private Node root = new Node();
// 在区间 [start, end] 中更新区间 [l, r] 的值,将区间 [l, r] ➕ val
// 如果结点表示为「区间最值」的情况时在更新结点时不需要✖️叶子节点的数量
// 下面的pushDown函数里也是 也要根据题目判断是否需要✖️叶子节点的数量
// 如果是「点更新」 也不需要✖️叶子节点的数量 因为此时区间是一个点所以一定会更新到叶子节点
// 本题是区间最值 区间为x轴的横轴 最值为对应区间内y轴上已有的最高的高度
public void update(Node node, int start, int end, int l, int r, int val) {
if (l <= start && end <= r) {
node.val = val;
node.add = val;
return ;
}
int mid = (start + end) >> 1;
pushDown(node, mid - start + 1, end - mid);
if (l <= mid) update(node.left, start, mid, l, r, val);
if (r > mid) update(node.right, mid + 1, end, l, r, val);
pushUp(node);
}
// 在区间 [start, end] 中查询区间 [l, r] 的结果, [l ,r] 保持不变
public int query(Node node, int start, int end, int l, int r) {
if (l <= start && end <= r) return node.val;
int mid = (start + end) >> 1, ans = 0;
pushDown(node, mid - start + 1, end - mid);
if (l <= mid) ans = query(node.left, start, mid, l, r);
if (r > mid) ans = Math.max(ans,query(node.right, mid + 1, end, l, r));
return ans;
}
// 向上更新
private void pushUp(Node node) {
node.val = Math.max(node.left.val , node.right.val);
}
// 推懒惰标记的函数
// 如果是「覆盖」的更新操作 则在下推懒惰标记的时候『不需要累加』
private void pushDown(Node node, int leftNum, int rightNum) {
if (node.left == null) node.left = new Node();
if (node.right == null) node.right = new Node();
if (node.add == 0) return ;
// 当前节点加上标记值✖️该子树所有叶子节点的数量 同上面update函数同步修改
node.left.val = node.add;
node.right.val = node.add;//这里俩个+=如果在点赋值时可以改成= 点累加不行
// 对区间进行「加减」的更新操作时,下推懒惰标记时需要累加起来,不能直接覆盖
node.left.add = node.add;
node.right.add = node.add;
node.add = 0;
}
}
力扣2407. 最长递增子序列 II
题目
public class Solution {
/*
在求解「上升子序列(IS)」问题时,一般有两种优化方法:
维护固定长度的 IS 的末尾元素的最小值 + 二分优化;
基于值域的线段树、平衡树等数据结构优化。
这两种做法都可以用 O(nlogn)的时间解决 300. 最长递增子序列。
对于本题,由于有一个差值不超过 kkk 的约束,用线段树更好处理。
具体来说,定义f[i][j]表示nums的前i个元素中,以元素j(注意不是 nums[j])结尾的满足题目两个条件的子序列的最长长度。
当j!=nums[i] f[i][j]=f[i-1][j]
当j==nums[i] f[i][j]=1+maxf[i-1][j'] 其中j'属于[j-k,j-1]
上式有一个「区间求最大值」的过程,这非常适合用线段树计算,且由于f[i]只会从 f[i−1]转移过来,我们可以把 f 的第一个维度优化掉
这样我们可以用线段树表示整个f 数组,在上面查询和更新。
最后答案为max(f[n-1]) 对应到线段树上就是根节点的值。
*/
public int lengthOfLIS(int[] nums, int k) {
int ans = 0;
for (int i = 0; i < nums.length; i++) {
// 查询上一轮f区间中以 [nums[i] - k, nums[i] - 1] 结尾的最长长度
// nums[i]的结尾不用查 因为要保证严格递增
int cnt = query(root, 0, N, Math.max(0, nums[i] - k), nums[i] - 1) + 1;
// 更新,注意这里是覆盖更新,对应的模版中覆盖更新不需要累加,已在下方代码中标注
update(root, 0, N, nums[i], nums[i], cnt);
ans = Math.max(ans, cnt);
}
return ans;
}
// *************** 下面是模版 ***************
class Node {
Node left, right;
int val, add;//线段树在[0, right]范围内的值tree.val表示以right值为结尾的序列的最长长度为tree.val
}
private int N = (int) 1e5;
private Node root = new Node();
public void update(Node node, int start, int end, int l, int r, int val) {
if (l <= start && end <= r) {
node.val = val; // 不需要累加
node.add = val; // 不需要累加
return ;
}
pushDown(node);
int mid = (start + end) >> 1;
if (l <= mid) update(node.left, start, mid, l, r, val);
if (r > mid) update(node.right, mid + 1, end, l, r, val);
pushUp(node);
}
public int query(Node node, int start, int end, int l, int r) {
if (l <= start && end <= r) return node.val;
pushDown(node);
int mid = (start + end) >> 1, ans = 0;
if (l <= mid) ans = query(node.left, start, mid, l, r);
if (r > mid) ans = Math.max(ans, query(node.right, mid + 1, end, l, r));
return ans;
}
private void pushUp(Node node) {
node.val = Math.max(node.left.val, node.right.val);
}
private void pushDown(Node node) {
if (node.left == null) node.left = new Node();
if (node.right == null) node.right = new Node();
if (node.add == 0) return ;
node.left.val = node.add; // 不需要累加
node.right.val = node.add; // 不需要累加
node.left.add = node.add; // 不需要累加
node.right.add = node.add; // 不需要累加
node.add = 0;
}
}
博主原链接,相对于本博客,本人加了一些个人理解和注释