二叉树
⼆叉树专题精讲
一、⼆叉树的理论基础
1.⼆叉树的种类
在我们解题过程中⼆叉树有两种主要的形式：满⼆叉树和完全⼆叉树。
满⼆叉树：如果⼀棵⼆叉树只有度为 0 的结点和度为 2 的结点，并且度为 0 的结点在同⼀层上，则这棵⼆叉树为满⼆叉树。
完全⼆叉树 ：在完全⼆叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最⼤值，并且最下⾯⼀层的节点都集中在该层最左边的若⼲位置。若最底层为第 h 层，则该层包含 1~ 2^h -1 个节点。
⼆叉搜索树 ： 前⾯介绍的树，都没有数值的，⽽⼆叉搜索树是有数值的了，⼆叉搜索树是⼀个有序树 。
- 若它的左⼦树不空，则左⼦树上所有结点的值均⼩于它的根结点的值；
- 若它的右⼦树不空，则右⼦树上所有结点的值均⼤于它的根结点的值；
- 它的左、右⼦树也分别为⼆叉排序树
平衡⼆叉搜索树：⼜被称为 AVL （ Adelson-Velsky and Landis ）树，且具有以下性质：它是⼀棵空树 它的左右两个⼦树的⾼度差的绝对值不超过1 ，并且左右两个⼦树都是⼀棵平衡⼆叉树。
如图:
2.⼆叉树的存储⽅式
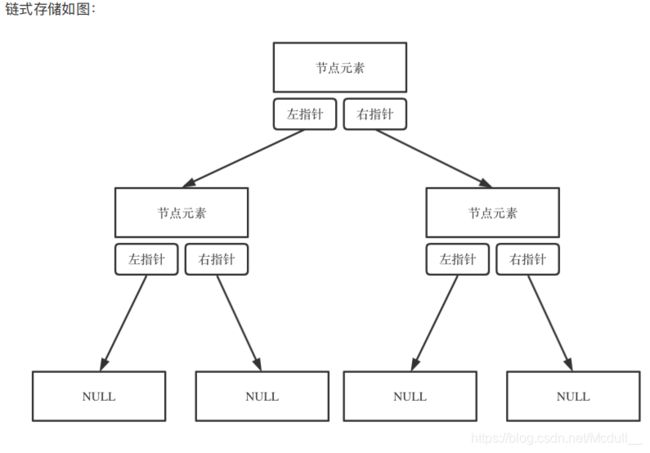
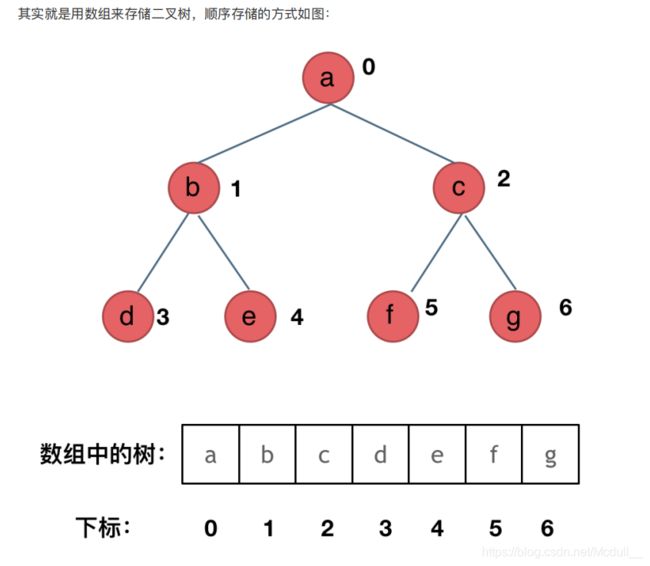
⼆叉树可以链式存储，也可以顺序存储.
那么链式存储⽅式就⽤指针， 顺序存储的⽅式就是⽤数组。
顺序存储:
⽤数组来存储⼆叉树如何遍历的呢？
如果⽗节点的数组下表是i，那么它的左孩⼦就是i * 2 + 1，右孩⼦就是 i * 2 + 2。
但是⽤链式表示的⼆叉树，更有利于我们理解，所以⼀般我们都是⽤链式存储⼆叉树。
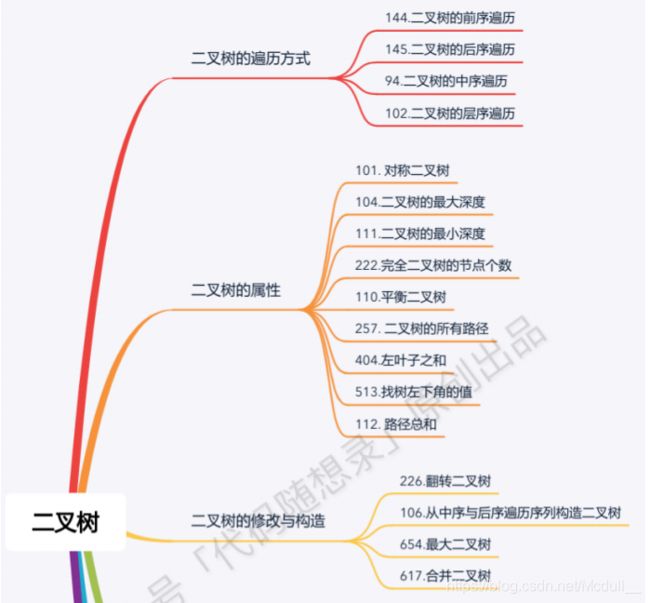
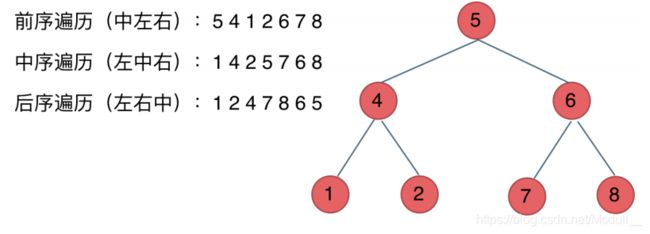
3.⼆叉树的遍历⽅式
⼆叉树主要有两种遍历⽅式：
（1）深度优先遍历：先往深⾛，遇到叶⼦节点再往回⾛。
- 前序遍历（递归法，迭代法） 【这⾥前中后，其实指的就是中间节点的遍历顺序，只要⼤家记住前中后序指的就a是中间节点的位置就可以了】
- 中序遍历（递归法，迭代法）
- 后序遍历（递归法，迭代法）
（2）⼴度优先遍历：⼀层⼀层的去遍历。
- 层次遍历（迭代法）
之前我们讲栈与队列的时候，就说过栈其实就是递归的⼀种是实现结构 ，也就说前中后序遍历的逻辑其实都是可以借助栈使⽤⾮递归的⽅式来实现的。
⽽⼴度优先遍历的实现⼀般使⽤队列来实现，这也是队列先进先出的特点所决定的，因为需要先进先出 的结构，才能⼀层⼀层的来遍历⼆叉树。
4.⼆叉树的定义
在现场⾯试的时候 ⾯试官可能要求⼿写代码，所以数据结构的定义以及简单逻辑的代码⼀定要锻炼⽩纸写出来。
值，左节点，右节点，无参构造，有一个值的参数构造，全参构造
public class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode() {}
TreeNode(int val) { this.val = val; }
TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}5.⼆叉树的递归遍历
递归算法的三个要素：
1. 确定递归函数的参数和返回值：
确定哪些参数是递归的过程中需要处理的，那么就在递归函数⾥加上这个参数， 并且还要明确每次递归的返回值是什么进⽽确定递归函数的返回类型。
2. 确定终⽌条件：
写完了递归算法 , 运⾏的时候，经常会遇到栈溢出的错误，就是没写终⽌条件或者终⽌条件写的不对，操作系统也是⽤⼀个栈的结构来保存每⼀层递归的信息，如果递归没有终⽌，操作系统的内存栈必然就会溢出。
3. 确定单层递归的逻辑：
确定每⼀层递归需要处理的信息。在这⾥也就会重复调⽤⾃⼰来实现递归的过程。
二、⼆叉树的遍历⽅式
二叉树的遍历方式 : 递归，迭代（栈）， 迭代（栈，统一写法）共9种
144.⼆叉树的前序遍历 https://leetcode-cn.com/problems/binary-tree-preorder-traversal/
145.⼆叉树的后序遍历 https://leetcode-cn.com/problems/binary-tree-postorder-traversal/solution/
94.⼆叉树的中序遍历 https://leetcode-cn.com/problems/binary-tree-inorder-traversal/
迭代（栈，统一写法）模板：以前序遍历为例。
//二叉树的前序遍历（迭代： 统一写法）
class Solution {
public List preorderTraversal(TreeNode root) {
List ans = new ArrayList<>();
Stack stack = new Stack<>();
if(root != null){
stack.push(root);
}
while(!stack.isEmpty()){
TreeNode node = stack.pop();//取出栈顶元素
if(node != null){
if(node.right != null){
stack.push(node.right);//添加右节点
}
if(node.left != null){
stack.push(node.left);//添加左节点
}
stack.push(node);//添加中节点
stack.push(null);//中节点访问过，但是还没有处理，加入空节点作为标记
}else{//只有遇到空节点（标志位）的时候，才将下一个节点放进结果集
node = stack.pop();//重新取出栈中元素
ans.add(node.val);
}
}
return ans;
}
} ⼆叉树的层序遍历
102.⼆叉树的层序遍历
题⽬地址： https://leetcode-cn.com/problems/binary-tree-level-order-traversal/
这道题可以作为模板
//广度优先遍历 队列
class Solution {
public List> levelOrder(TreeNode root) {
List> ans = new ArrayList<>();
Queue queue = new LinkedList<>();
if(root != null){
queue.offer(root);//添加元素offer 弹出元素 poll
}
while(!queue.isEmpty()){
int size = queue.size();
List res = new ArrayList<>();
for(int i=0;i
下面这几道题都可以套上面的模板：
107.⼆叉树的层次遍历 II （在模板的基础上增加一个反转即可）
题⽬链接： https://leetcode-cn.com/problems/binary-tree-level-order-traversal-ii/
199. ⼆叉树的右视图
题⽬链接： https://leetcode-cn.com/problems/binary-tree-right-side-view/
637. ⼆叉树的层平均值
题⽬链接： https://leetcode-cn.com/problems/average-of-levels-in-binary-tree/
429.N 叉树的层序遍历
题⽬链接： https://leetcode-cn.com/problems/n-ary-tree-level-order-traversal/
515. 在每个树⾏中找最⼤值
题⽬链接： https://leetcode-cn.com/problems/find-largest-value-in-each-tree-row/
116. 填充每个节点的下⼀个右侧节点指针
题⽬链接： https://leetcode-cn.com/problems/populating-next-right-pointers-in-each-node/
117. 填充每个节点的下⼀个右侧节点指针 II
题⽬地址： https://leetcode-cn.com/problems/populating-next-right-pointers-in-each-node-ii/
三、⼆叉树的属性
对称⼆叉树：
递归：后序，⽐较的是根节点的左⼦树与右⼦树是不是相互翻转迭代：使⽤队列 / 栈将两个节点顺序放⼊容器中进⾏⽐较
101. 对称⼆叉树
题⽬地址： https://leetcode-cn.com/problems/symmetric-tree/
100. 相同的树
题⽬地址： https://leetcode-cn.com/problems/same-tree/
572. 另⼀个树的⼦树
题⽬地址： https://leetcode-cn.com/problems/subtree-of-another-tree/
⼆叉树的最⼤深度：
递归：后序，求根节点最⼤⾼度就是最⼤深度，通过递归函数的返回值做计算树的⾼度迭代：层序遍历
104.⼆叉树的最⼤深度
题⽬地址：https://leetcode-cn.com/problems/maximum-depth-of-binary-tree/
559.N叉树的最⼤深度
题⽬地址：https://leetcode-cn.com/problems/maximum-depth-of-n-ary-tree/
⼆叉树的最⼩深度：
递归：后序，求根节点最⼩⾼度就是最⼩深度，注意最⼩深度的定义迭代：层序遍历
111.⼆叉树的最⼩深度
题⽬地址： https://leetcode-cn.com/problems/minimum-depth-of-binary-tree/
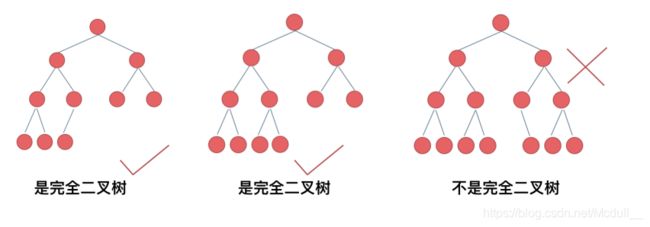
完全⼆叉树的节点个数 ：
递归：后序，通过递归函数的返回值计算节点数ᰁ迭代：层序遍历
222.完全⼆叉树的节点个数
题⽬地址：https://leetcode-cn.com/problems/count-complete-tree-nodes/
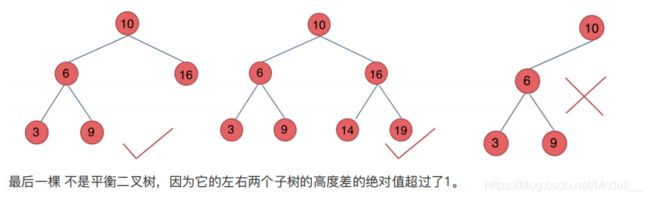
平衡⼆叉树：
递归：后序，注意后序求⾼度和前序求深度，递归过程判断⾼度差迭代：效率很低，不推荐
110.平衡⼆叉树
题⽬地址：https://leetcode-cn.com/problems/balanced-binary-tree/
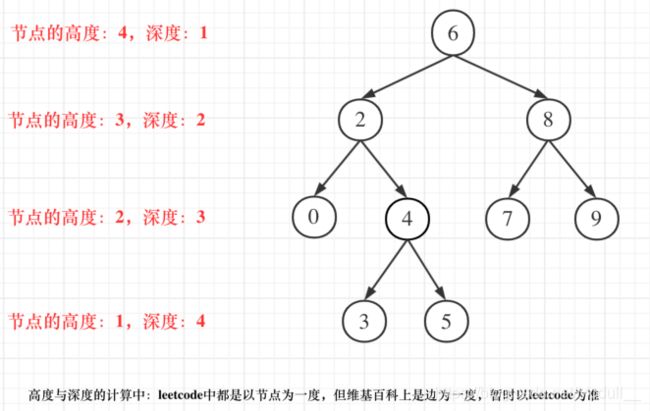
高度和深度：根节点的⾼度就是这颗树的最⼤深度
求深度可以从上到下去查 所以需要前序遍历（中左右），⽽⾼度只能从下到上去查，所以只能后序遍历（左右中）
⼆叉树的所有路径：
递归：前序，⽅便让⽗节点指向⼦节点，涉及回溯处理根节点到叶⼦的所有路径迭代：⼀个栈模拟递归，⼀个栈来存放对应的遍历路径
257. ⼆叉树的所有路径
题⽬地址：https://leetcode-cn.com/problems/binary-tree-paths/
左叶⼦之和：
递归：后序，必须三层约束条件，才能判断是否是左叶⼦。迭代：直接模拟后序遍历
404. 左叶⼦之和
题⽬地址： https://leetcode-cn.com/problems/sum-of-left-leaves/
树左下⻆的值：
递归：顺序⽆所谓，优先左孩⼦搜索，同时找深度最⼤的叶⼦节点。迭代：层序遍历找最后⼀⾏最左边
513.找树左下⻆的值
题⽬地址：https://leetcode-cn.com/problems/find-bottom-left-tree-value/
如果需要遍历整颗树，递归函数就不能有返回值。如果需要遍历某⼀条固定路线，递归函数就⼀定要有返回值！
路径总和：
递归：顺序⽆所谓，递归函数返回值为 bool 类型是为了搜索⼀条边，没有返回值是搜索整棵树。迭代：栈⾥元素不仅要记录节点指针，还要记录从头结点到该节点的路径数值总和
112. 路径总和
题⽬地址：https://leetcode-cn.com/problems/path-sum/
113. 路径总和II
题⽬地址：https://leetcode-cn.com/problems/path-sum-ii/
四、⼆叉树的修改与构造
翻转⼆叉树：
递归：前序，交换左右孩⼦迭代：直接模拟前序遍历
226. 翻转⼆叉树 （四种方法对二叉树的遍历进行总结）
题⽬地址： https://leetcode-cn.com/problems/invert-binary-tree/
构造⼆叉树登场：
递归：前序，重点在于找分割点，分左右区间构造迭代：⽐较复杂，意义不⼤
106.从中序与后序遍历序列构造⼆叉树
题⽬地址：https://leetcode-cn.com/problems/construct-binary-tree-from-inorder-and-postorder-traversal/
105.从前序与中序遍历序列构造⼆叉树
题⽬地址：https://leetcode-cn.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal/
前序和中序可以唯⼀确定⼀颗⼆叉树。
后序和中序可以唯⼀确定⼀颗⼆叉树。
那么前序和后序可不可以唯⼀确定⼀颗⼆叉树呢？
前序和后序不能唯⼀确定⼀颗⼆叉树！ ，因为没有中序遍历⽆法确定左右部分，也就是⽆法分割。
构造⼀棵最⼤的⼆叉树：
递归：前序，分割点为数组最⼤值，分左右区间构造迭代：⽐较复杂，意义不⼤
654.最⼤⼆叉树
题⽬地址：https://leetcode-cn.com/problems/maximum-binary-tree/
注意类似⽤数组构造⼆叉树的题⽬，每次分隔尽量不要定义新的数组，⽽是通过下表索引直接在原数组上操作，这样可以节约时间和空间上的开销。
合并两个⼆叉树：
递归：前序，同时操作两个树的节点，注意合并的规则迭代：使⽤队列，类似层序遍历
617. 合并⼆叉树
题⽬地址： https://leetcode-cn.com/problems/merge-two-binary-trees/
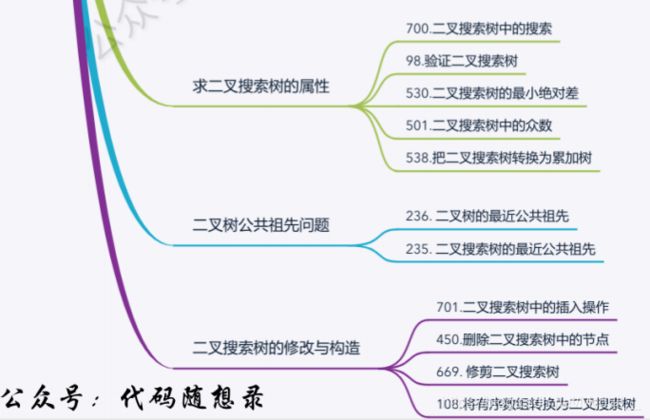
五、求⼆叉搜索树的属性
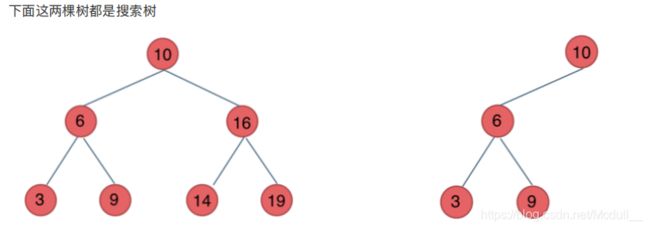
⼆叉搜索树中的搜索：
递归：⼆叉搜索树的递归是有⽅向的迭代：因为有⽅向，所以迭代法很简单
700. ⼆叉搜索树中的搜索
题⽬地址： https://leetcode-cn.com/problems/search-in-a-binary-search-tree/
⼆叉搜索树是⼀个有序树：
- 若它的左⼦树不空，则左⼦树上所有结点的值均⼩于它的根结点的值；
- 若它的右⼦树不空，则右⼦树上所有结点的值均⼤于它的根结点的值；
- 它的左、右⼦树也分别为⼆叉搜索树
验证⼆叉搜索树：
递归：中序，相当于变成了判断⼀个序列是不是递增的迭代：模拟中序，逻辑相同
98.验证⼆叉搜索树
题⽬地址：https://leetcode-cn.com/problems/validate-binary-search-tree/
注意⼆叉搜索树中不能有重复元素
(⼆叉搜索树的特性)⼆叉搜索树的最⼩绝对差：
递归：中序，双指针操作迭代：模拟中序，逻辑相同
530. ⼆叉搜索树的最⼩绝对差
题⽬地址： https://leetcode-cn.com/problems/minimum-absolute-difference-in-bst/
⼆叉搜索树中的众数：
递归：中序，清空结果集的技巧，遍历⼀遍便可求众数集合迭代：模拟中序，逻辑相同
501. ⼆叉搜索树中的众数
题⽬地址： https://leetcode-cn.com/problems/find-mode-in-binary-search-tree/solution/
把⼆叉搜索树转换为累加树：
递归：中序，双指针操作累加迭代：模拟中序，逻辑相同
538. 把⼆叉搜索树转换为累加树
题⽬链接： https://leetcode-cn.com/problems/convert-bst-to-greater-tree/
六、⼆叉树公共祖先问题
⼆叉树的最近公共祖先：
递归：后序，回溯，找到左⼦树出现⽬标值，右⼦树节点⽬标值的节点。迭代：不适合模拟回溯
236. ⼆叉树的最近公共祖先
题⽬链接：https://leetcode-cn.com/problems/lowest-common-ancestor-of-a-binary-tree/
⼆叉搜索树的最近公共祖先：
递归：顺序⽆所谓，如果节点的数值在⽬标区间就是最近公共祖先迭代：按序遍历
235. ⼆叉搜索树的最近公共祖先
链接： https://leetcode-cn.com/problems/lowest-common-ancestor-of-a-binary-search-tree/
七、⼆叉搜索树的修改与构造
⼆叉搜索树中的插⼊操作：
递归：顺序⽆所谓，通过递归函数返回值添加节点迭代：按序遍历，需要记录插⼊⽗节点，这样才能做插⼊操作
701. ⼆叉搜索树中的插⼊操作
链接： https://leetcode-cn.com/problems/insert-into-a-binary-search-tree/
删除⼆叉搜索树中的节点：
递归：前序，想清楚删除⾮叶⼦节点的情况迭代：有序遍历，较复杂
450.删除⼆叉搜索树中的节点 （比插入复杂，因为因为⼆叉搜索树添加节点只需要在叶⼦上添加就可以的，不涉及到结构的调整，⽽删除节点操作涉及到结构的调整）
题⽬链接： https://leetcode-cn.com/problems/delete-node-in-a-bst/
修剪⼆叉搜索树：
递归：前序，通过递归函数返回值删除节点迭代：有序遍历，较复杂
669. 修剪⼆叉搜索树
题⽬链接： https://leetcode-cn.com/problems/trim-a-binary-search-tree/
构造⼀棵⼆叉搜索树：
递归：前序，数组中间节点分割迭代：较复杂，通过三个队列来模拟
108.将有序数组转换为⼆叉搜索树(本质就是寻找分割点，分割点作为当前节点，然后递归左区间和右区间 。)
题⽬链接： https://leetcode-cn.com/problems/convert-sorted-array-to-binary-search-tree/
八、总结
- 涉及到⼆叉树的构造，⽆论普通⼆叉树还是⼆叉搜索树⼀定前序，都是先构造中节点。
- 求普通⼆叉树的属性，⼀般是后序，⼀般要通过递归函数的返回值做计算。
- 求⼆叉搜索树的属性，⼀定是中序了，要不⽩瞎了有序性了。
注意在普通⼆叉树的属性中，我⽤的是⼀般为后序，例如单纯求深度就⽤前序， ⼆叉树：找所有路径 也⽤了前序，这是为了⽅便让⽗节点指向⼦节点。 所以求普通⼆叉树的属性还是要具体问题具体分析。