《数据结构》上机实验(第六章) —数组和广义表
1. 利用数组求解约瑟夫问题：设有n个人站成一圈，其编号为1~n。从编号为1的人开始按顺时针方向“1,2,3,4,…"循环报数，数到m的人出列，然后从出列者的下一个人重新开始报数，数到m的人又出列，如此重复进行，直到m个人都出列为止，要求输出这n个人的出列顺序。
- 算法思想：采用一维数组arr[]存放人的编号，先将n个人的编号存入到arr[0]~arr[n-1]中。从编号为1的人(下标=0)开始循环报数，数到m的人arr[t](下标=(t+m-1)%i，i表示当前未出列的人数)输出并将其从数组中删除(即将后面的元素前移一个位置)，因此每次报数的起始位置就是上次报数的出列位置。反复执行直到出列n个人为止。
void josephus(int n, int m)
{
int i, j, arr[MaxSize];
for (i = 0; i < n; i++) arr[i] = i + 1;
int t = 0;
for (i = n; i > 0; i--)
{
t = (t + m - 1) % i;
printf("%d ", arr[t]);
for (j = t + 1; j < n; j++) arr[j-1] = arr[j];
}
}
运行结果
2. 设计一个用于存储双层集合的存储结构，所谓双层集合是指这样的集合：其中每个元素又是一个集合(称为集合元素)，该集合元素由普通的整数元素构成。例如S={{1,3},{1,7,8},{5,6}}。
- 算法思想：采用类似于十字链表的思路，将每个集合元素设计成带头结点的单链表，将这些集合元素头结点串起来构成一个单链表，设置h所指的结点作为集合头结点。
数据结点的类型声明：
typedef struct dnode
{
int data;
struct dnode *next;
}DType;
集合元素头结点的类型声明：
typedef struct hnode
{
DType *next;
struct hnode *link;
}HType;
3. 假设n×n的稀疏矩阵A采用三元组表示。
（1）生成以下两个稀疏矩阵的三元组a和b
[ 1 0 3 0 0 1 0 0 0 0 1 0 0 0 1 1 ] \begin{bmatrix} 1 & 0 & 3 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 1 & 1\\ \end{bmatrix} ⎣⎢⎢⎡1000010030110001⎦⎥⎥⎤
[ 3 0 0 0 0 4 0 0 0 0 1 0 0 0 0 2 ] \begin{bmatrix} 3 & 0 & 0 & 0\\ 0 & 4 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 2\\ \end{bmatrix} ⎣⎢⎢⎡3000040000100002⎦⎥⎥⎤
void DispMat(TSMatrix t)
{
if (t.nums <= 0) return;
printf("\t%d\t%d\t%d\n", t.rows, t.cols, t.nums);
printf("\t------------------\n");
for (int i = 0; i < t.nums; i++)
printf("\t%d\t%d\t%d\n", t.data[i].r, t.data[i].c, t.data[i].d);
}
void CreateMat(TSMatrix &t,ElemType A[M][N])
{
t.cols = M;
t.rows = N;
t.nums = 0;
for (int i = 0; i < M; i++)
for (int j = 0; j < N; j++)
{
if (A[i][j] != 0)
{
t.data[t.nums].d = A[i][j];
t.data[t.nums].r = i;
t.data[t.nums].c = j;
t.nums++;
}
}
}
（2）输出a转置矩阵的三元组
void TranTat(TSMatrix t, TSMatrix& ta)
{
int k1=0;
if (t.nums <= 0) return;
ta.cols = t.cols;
ta.rows = t.rows;
ta.nums = t.nums;
for(int v=0;v<t.cols;v++)
for (int k = 0; k < t.nums; k++)
{
if (t.data[k].c == v)
{
ta.data[k1].r = t.data[k].c;
ta.data[k1].c = t.data[k].r;
ta.data[k1].d = t.data[k].d;
k1++;
}
}
}
（3）输出a+b的三元组
bool SumMat(TSMatrix a, TSMatrix b, TSMatrix &c)
{
int i = 0, j = 0, k = 0;
ElemType v;
if (a.rows != b.rows || a.cols != b.cols) return false; //行数或列数不等时不能进行相加运算
c.cols = a.cols; c.rows = a.rows; //c的行列数与a的相同
while (i < a.nums && j < b.nums) //处理a和b中的每一个元素
{
if (a.data[i].r == b.data[j].r) //行号相等时
{
if (a.data[i].c < b.data[j].c) //a元素的列号小于b元素的列号
{
c.data[k].r = a.data[i].r; //将a元素添加到c中
c.data[k].c = a.data[i].c;
c.data[k].d = a.data[i].d;
k++; i++;
}
else if (a.data[i].c > b.data[j].c) //a元素的列号大于b元素的列号
{
c.data[k].r = b.data[j].r; //将b元素添加到c中
c.data[k].c = b.data[j].c;
c.data[k].d = b.data[j].d;
k++; j++;
}
else //a元素的列号等于b元素的列号
{
v = a.data[i].d + b.data[j].d;
if (v != 0) //只将不为0的结果添加到c中
{
c.data[k].r = a.data[i].r;
c.data[k].c = a.data[i].c;
c.data[k].d = v;
k++;
}
i++; j++;
}
}
else if (a.data[i].r < b.data[j].r) //a元素的行号小于b元素的行号
{
c.data[k].r = a.data[i].r; //将a元素添加到c中
c.data[k].c = a.data[i].c;
c.data[k].d = a.data[i].d;
k++; i++;
}
else //a元素的行号大于b元素的行号
{
c.data[k].r = b.data[j].r; //将b元素添加到c中
c.data[k].c = b.data[j].c;
c.data[k].d = b.data[j].d;
k++; j++;
}
c.nums = k;
}
return true;
}
4. 求n×n阶螺旋方阵(按顺时针方向旋进)。
- 算法思想：fun(int a[][],int n)：用二维数组a存放m阶螺旋方阵。m阶螺旋方阵共有[n/2]圈，对于第i(0≤i≤m-1共执行m次)圈循环，产生该圈上横行的数字，产生该圈右竖行的数字，产生该圈下横行的数字，产生该圈左竖行的数字。最后输出该方阵。
#include
5. 求矩阵的马鞍点。(如果矩阵A中存在这样的一个元素，满足条件：A[i][j]是第i行中值最小的元素，且又是第j列中值最大的元素，则称之为该矩阵的一个马鞍点。)
- 算法思想：MinMax(int A[][])：先求出每行的最小值元素，放人min[m]中，再求出每列的最大值元素，放入max[n]中，若某元素既在min[i]中，又在max[j]中，则该元素A[i][j]便是马鞍点。
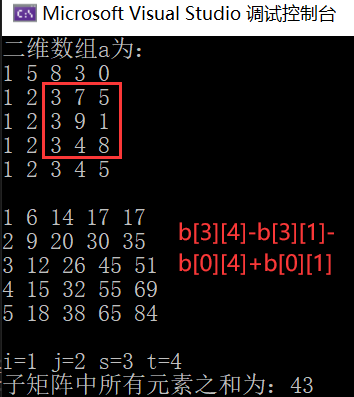
#include
6. 假设有一个m行n列的二维数组a，其中所有元素为整数。其大量的运算是求左上角为a[i,j]、右下角为a[s,t](i
- 算法思想：建立一个m行n列的二维数组b，b[i,j]为a中左上角为a[0,0]、右下角为a[i,j]的子矩阵的所有元素之和。
void sum(ElemType a[][MaxSize], ElemType b[][MaxSize], int m, int n)
{
int i, j;
b[0][0] = a[0][0];
for (i = 1; i < m; i++) b[i][0] = b[i - 1][0] + a[i][0]; //求b的第0列
for (j = 1; j < n; j++) b[0][j] = b[0][j-1] + a[0][j]; //求b的第0行
for (i = 1; i < m; i++) //求b[i][j]
for (j = 1; j < n; j++)
b[i][j] = a[i][j] + b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];
}
- 该算法的时间复杂度为O(m×n)。在求出b数组后，求数组a中左上角为a[i][j]、右下角为a[s][t]的子矩阵的所有元素之和就可以利用数组b来实现，其值为b[s][t] - b[s][j - 1] - b[i - 1][t] + b[i - 1][j - 1]。
ElemType submat(ElemType b[][MaxSize], int i, int j, int s, int t)
{
if (s == 0 && j == 0) return b[s][t];
return b[s][t] - b[s][j - 1] - b[i - 1][t] + b[i - 1][j - 1];
}
- 显然该算法的时间复杂度为O(1)。尽管sum算法的时间复杂度为O(m×n)，但只需要执行一次，而submit算法需要大量应用，所以这种设计是十分经济的。
7. (1)设有一个整型数组a，使a[i]的值变为a[0]到a[i-1]中小于原a[i]值的个数。
- 算法思想：i从n-1到0循环，累计a[0…i-1]中大于a[i]的元素个数c，置a[i]为c。本算法的时间复杂度为 O ( n 2 ) O(n^2) O(n2)。
void fun(ElemType arr[MaxSize], int n)
{
int i, j, count;
for (i = n - 1; i >= 0; i--)
{
count = 0;
for (j = 0; j < i; j++)
if (arr[j] < arr[i]) count++;
arr[i] = count;
}
}
(2)设有一个元素递增的整型数组a，且所有元素均不相同。使a[i]的值变为a[0]到a[i-1]中小于原a[i]值的个数。
- 算法思想：由于数组a中元素递增且所有元素均不相同，置a[0]=0，用i从0到n-1循环。temp保存[i-1]元素值，若a[i]>temp，置a[i]=a[i-1]+1，否则a[i]=a[i-1]。本算法的时间复杂度为O(n)。
void fun(ElemType arr[MaxSize], int n)
{
int i, j, temp = arr[0];
arr[0] = 0;
for (i = 1; i < n; i++)
{
if (arr[i] > temp) arr[i] = arr[i - 1] + 1;
else arr[i] = arr[i - 1];
}
}
8. 给定有n(n≥1)个整数的序列用整型数组a存储，要求求出其中最大连续子序列的和。
- 算法思想：设含有n个整数的序列a[0…n-1]的任何连续子序列a[i…j](i≤j,0≤i≤n-1,i≤j≤m-1)，求出它的所有元素之和thisSum，并通过比较将最大值存放在maxSum中，最后返回maxSum。
long maxSubSum1(int a[], int n)
{
int i, j, k, thisSum, maxSum = a[0];
for (i = 0; i < n; i++) //两重循环穷举所有的连续子序列
for (j = i; j < n; j++)
{
thisSum = 0;
for (k = i; k <= j; k++)
{
thisSum = thisSum + a[k];
if (thisSum > maxSum) maxSum = thisSum; //通过比较求最大连续子序列之和
}
}
return maxSum;
}
- 本算法穷举所有连续子序列(连续子序列由起始下标和终止下标j确定)来求解，用了三重循环，所以时间复杂度为 O ( n 3 ) O(n^3) O(n3)。
9. 将一维数组A[0…n×n-1](n≤10)中的元素按蛇形方式存放在二维数组B[0…m-1,0…n-1]中。
- 算法思想：以n=4为例，其中有7条斜线，每条斜线的元素个数为gs，奇数斜线的元素编号从下向上递增，偶数斜线的元素编号从上向下递增。
void fun(ElemType a[n], ElemType b[][n])
{
int i, j, k, m = 0, g, gs;
for (k = 1; k <= 2 * n - 1; k++) //对于每条对角线循环一次
{
if (k < n) gs = k; //gs为第k条斜线上的元素个数
else gs = 2 * n - k;
for (g = 1; g <= gs; g++)
{
if (k % 2 == 1) //k为奇数的情况，从下向上递增
{
i = gs - g;
j = g-1;
}
else //k为偶数的情况，从上向下递增
{
i = g-1;
j = gs - g;
}
if (k > n) //考虑第n+1到2n-1的斜线
{
i = i + n - gs;
j = j + n - gs;
}
b[i][j] = a[m++];
}
}
}
