联邦学习综述（二）

二、用Shapley值解释联邦学习模型

2.1 Shapley值

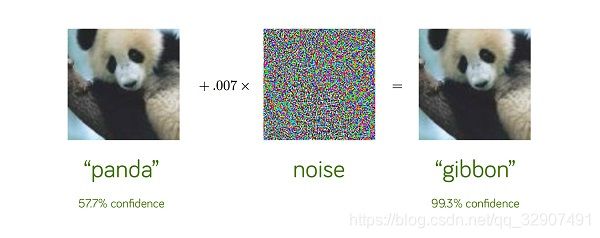
我们知道机器学习模型很多都是黑盒或者半黑盒模型。如果模型是用来做语音识别、图像识别之类的感知任务，可能人们就不会太过关心模型的可解释性问题；当然也有很多对抗学习的工作在研究感知模型，想必很多人对那个熊猫加没信号的电视机就变成长臂猿的例子记忆犹新，但这些工作可能更多是从模型可靠性的角度出发。

对于另一些关键应用中的非感知类的机器学习模型，比如贷款风险估算，保险核保预测，欺诈识别模型等等，模型的可解释性就尤为重要。博客“Algorithms Auditing：你的代码公平正义吗？”里面有大致聊过一些机器学习模型审计的重要性和一些方法。其中提到一个很有意思的独立于模型算法的模型解释方法就是用Shapley值来计算模型特征的重要性，也是SHAP这个工具包背后的重要思想。SHAP以已经被很多做金融和保险机器学习模型的同僚们应用在实际工作中了，瓶颈可能不在技术而更多在于如何给合规与法律部门的同事解释清楚这个东西到底是怎么回事。

我们假设已经训练好了一个模型$f(x)$，把特征向量x映射去一个预测值$y$，这里$x$包含了$n$个不同的特征，$x=x1,x2,\dots ,xn$。我们想知道每一个特征在这个模型中的起到了怎样的作用。这包含了两个层面：我们可以对每一个单独的预测感兴趣，用特征重要程度来试图解释每一个特定的决策；我们也可以对整个模型感兴趣，想知道每个特征在模型做出大量决策时的重要度。对于后者，也就是整个模型的特征重要性，其实如xgboost这样的工具包已经包含了类似的功能。SHAP更多是聚焦于前者。实际应用中对单个决策的解释也是非常重要，因为人们会问凭什么你给李雷放了贷款而不给我放，凭什么韩梅梅的保费就是比我低等等这样的问题。

Shapley值源自于博弈论，应用在模型解释性的思路也是很直接了当。模型$f$已经有了，对于一个特定决策，所有特征$x_1,x_2,\dots ,x_n$的具体值也在。我们把每个特征当作一个开关，尝试构造一系列模拟的特征值，每一次都把$x_1,x_2,\dots ,x_n$中的一些特征“开启”和“关掉”，然后计算预测结果和原始结果的偏差。当我们尝试尽所有可能的特征“开启”和“关掉”的组合，就有了一系列这样的偏差值。我们现在要计算特征$x_i$的重要性，只要参考除了$x_i$之外的其它所有特征排列组合下，$x_i$关掉和开启的两种情况对原始结果造成的平均波动就好了。

这样的思路，就是完全把模型当作一个黑盒子，不管你的盒子是神经网络做的还是随机森林做的，不断尝试拔掉和接上炸弹上面有颜色的电线，观察爆炸的猛烈程度来判断哪个电线是重要的哪个是没用的…

举个例子：首先思考这样一个问题：

小明，小军，小强（是的，就是他们，小学课本三人组），组队参加王者农药大赛，大赛设定哪个队先拿100个人头，可以获得一万元奖金。终于在他们三个的通力配合下，赢得了比赛，获得一万元奖金，但到了分钱阶段，分歧出现了，因为他们三个人的水平、角色不一，小强个人实力最强善用高输出角色，光是他自己就拿了大半的人头；但若是按照人头数分，也不合适，因为前期小强有几次差点挂掉，多亏队友及时治疗，另外有好多人头也是靠攻速抢到的。那么，应该怎么分配这一万块钱，才是最公平的呢？

机智（厚脸皮）的小老弟登场了，这个问题，我们可以从贡献出发：

小强自己可以干掉35个人，小军可以干掉15个人，小明可以干掉10个人，显然，他们每个人都无法独立完成目标。

小强和小军联手可以干掉70个人，小强和小明可以干掉60个人，小军和小明联手可以干掉40个人，同样，无法完成任务。

而只有当三个人联手时候，才可以干掉100个人，达成目标。

（可以理解为小军小强小明有辅助有输出有坦克）

考虑先后顺序，他们三个人一共有6种组队方式。

我们定义边际贡献：假定初始组合为小强一个人，贡献35，加入小军后，他们俩的组合贡献为70，则小军的边际贡献就是70-35=35，再加入小明，三个人的组合贡献为100，则小明的边际贡献为100-70=30；

根据组合次序计算全部的组合及组合中每个人的边际贡献，如表格所示，则可以求得每个人的贡献度。

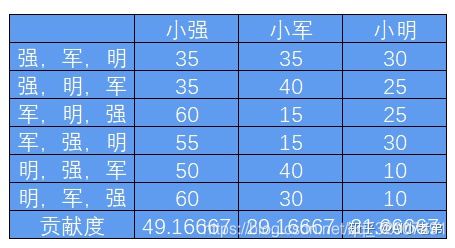
因此，最合理的分配方案就是小强小军小明分别获得4916、2917、2167。

大家可能奇怪上面的故事和本文主题有啥关系，实际上，上面的问题就是通俗的解释了SHAP方法的核心：shapley value(沙普利值)的简化版计算方法。表格中的贡献度即为SHAP值，代表每个人的贡献度。

关于SHAP值的计算参考：XGB模型可解释性SHAP包实战

2.2 联邦学习

在博客如“为什么保险行业需要联邦学习”中也有简单介绍。联邦学习的目标是能让多个数据拥有方在不暴露自己数据内容的情况下联合建模解决问题。 最早提出这个概念的谷歌把联邦学习应用在Gboard输入法中。用户在自己的手机上用自己的键盘数据训练一个输入法模型，然后用户的模型(而不是用户数据)会汇总到谷歌的服务器上做模型融合，模型再推送回给用户，如此迭代更新，用户在不牺牲自己键盘数据的情况下群体合作帮助谷歌训练出一个强大的Gboard输入法，帮你纠错和预测你下一步要输入的词。

谷歌的例子中，所有用户的特征空间是一致的，而用户ID之间没有重叠，这是对应于横向联邦学习的范畴。另一种纵向联邦学习的场景是对应于几方数据拥有者有重叠的用户ID，而分别掌控着不同的特征空间。一个例子是银行和电商的合作：银行拥有用户的金融特征信息，电商拥有用户的购买行为的特征信息。两方合作可以对用户有更全面的特征刻画，而纵向联邦学习可以让双方在不暴露自己具体数据的情况下针对双方不同的场景（不同预测目标）训练出更强大的机器学习模型。

对于横向联邦学习，模型的可解释性与普通机器学习并无两样，因为每个样本的全体特征数据依然掌握在同一方里。对于纵向联邦学习，解释某一个决策结果就是给出每一个预测的每一个特征的权重信息，很大可能会暴露出每个样本的另一方的特征数据。

所以这篇文章准确来讲是如何解释纵向联邦学习，在多方数据隐私保护和模型可解释性中寻找到一个平衡。

解释纵向联邦学习
对于A和B一起建立的纵向联邦学习模型，设想我们站在A的角度想做模型解释，我们自然希望A拥有的所有特征重要性都能尽可能准确和详细地展示出。因为B的特征值A并不能拿到，所以折衷起见我们希望能将B的所有特征集合成为一个大的特征，我们称为联邦特征，然后计算出这个B的联邦特征的权重值。

写到这里，结合Shapley值的介绍，可能各位已经猜到我们的做法。我们不再是对A和B的所有特征做排列组合和开启关闭，而是对A的所有特征和B的这一个大的联邦特征做排列组合，然后计算这些特征的Shapley值，期待我们能准确找到A的特征权重的同时，也能对B的特征权重有一个总体的认识。

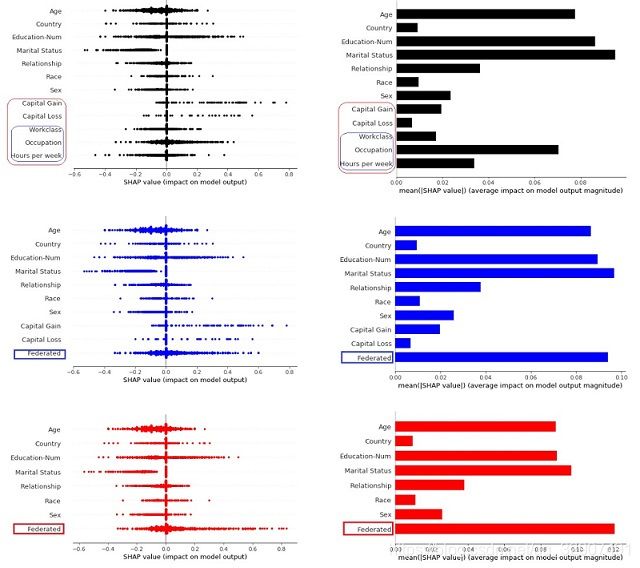
我们找了一个公开数据集来做实验，数据集用来预测一个人是否有钱（…）。特征里面包括了年龄、性别、种族、国家、教育信息这样的特征，还包括了过去一年的投资收成、工作等级、职位和每周工作时间这样的特征。我们使用Shapley值首先计算所有特征的权重值作为Ground Truth参考。然后模拟纵向联邦学习，将3个工作相关的特征作为B的联邦特征进行权重值计算，与Ground Truth进行比较。我们又加入投资成果与工作相关特征一共5个特征作为B的联邦特征进行计算，在联邦特征占据更多特征空间的情况下再次比较。单个预测的特征权重点和所有预测每个特征的平均权重结果如下：

可以看到虽然有一些特征被聚合成为联邦特征，失去了部分特征的细节粒度信息，但对于不需隐藏的A的几个特征，无论是单个预测的特征权重值分布还是全部预测每个特征的平均权重值，都很好地复现了没有联邦学习之前A的结果。而对于B，联邦特征的值也在不需要暴露特征具体信息的情况下比较好地总结了B的所有特征空间对模型预测的贡献。加入更多特征到联邦特征的集合里，也依然得到比较好的结果，显示我们提出的算法有一定的稳定性。

无论联邦学习还是模型可解释性，都是学术界研究的前沿问题。这里的工作只是联邦学习模型可解释性研究的冰山一角。Shapley值是一个独立于模型细节的模型解释方法，而各种机器学习算法要针对联邦学习做相应的适配，针对特定模型比如广义线性模型和树模型的联邦学习的解释方法，都是对现有模型解释算法的拓展，是未来可以继续研究的有趣方向。

参考文献：

1. Interpret Federated Learning with Shapley Values
2. A Principled Approach to Data Valuation for Federated Learning
3. 用Shapley值解释联邦学习模型代码