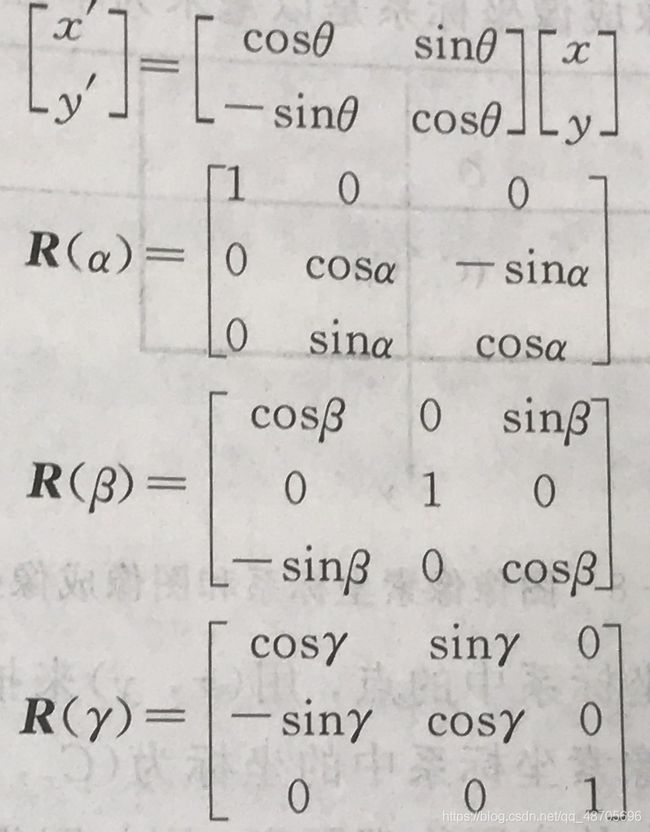Halcon_标定
转自:(2条消息) Halcon_标定_halcon标定_x1angzeeD.的博客-CSDN博客
在机器视觉领域中,为了确定空间物体表面某点的三维几何位置与其投影图像(二维)中对应点之间的关系,必须建立相机成像的几何模型,这些几何模型参数就是相机的内外参数。在大多数条件下,这些参数必须通过实验与计算才能得到,这个求解参数的过程称为标定(或者相机标定)。无论是在机器视觉还是在图像测量应用中,相机参数的标定都是非常关键的环节,其标定结果的精度及算法的稳定性直接影响结果的准确性。因此做好相机标定是进行后续工作及实验的前提。
标定的目的:
相机需要标定的原因之一就是镜头畸变。所有光学相机镜头都存在畸变问题,畸变属于成像的几何失真,它是由于焦平面上不同区域对影像的放大率不同而形成的画面扭曲变形现象,这种变形的程度从画面中心至画面边缘依次递增,主要在画面边缘反映得较为明显。
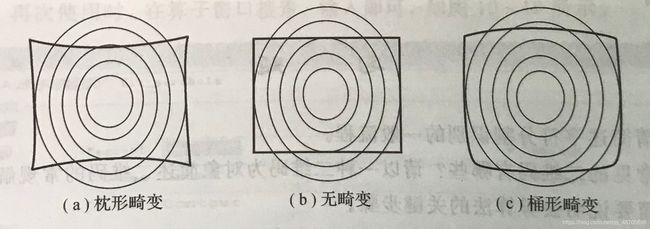
镜头畸变分为桶形畸变和枕形畸变,也有的分为径向畸变和梯形畸变
大多数镜头都有径向畸变,而切向畸变影响相对较小。
在正常拍摄的情况下,矩形物体的像仍是矩形。如果将矩形物体拍摄成四边向外凸形成桶形的影像,就称镜头具有负畸变或桶形畸变。相反,如果影像为四边凹进,称镜头具有正畸变或枕形畸变。桶形畸变是由于视场边缘的放大率比中心部分低所引起的,即便缩小光圈也不能矫正;枕形畸变是由于视场边缘部分的放大率比中心部分高所引起的,即倾斜角度大的光线的放大率比倾斜角度小的光线的放大率高。相机标定就是为了消除相机镜头在拍摄过程中产生的畸变。
标定理论
一、计算机视觉中的各种坐标系
在图像测量、定位过程以及其他机器视觉应用中,为确定空间物体表面某点的三维成何位置与其在图像中对应点之间的相互关系,必须建立相机成像的几何模型,这些几何模型参数就是相机参数。这个求解参数的过程就称为相机标定。
求解出镜头的畸变参数,就可以把有畸变的图像变换到没有畸变状态的图像。
首先了解针孔相机模型,真实世界(世界坐标系)的某点通过相机、镜头和图像采集设备映射到二维图像。
在相机的成像模型中,包含有几个坐标系:世界坐标系、相机坐标系、图像坐标系。相机成像过程的数学模型就是目标点在这几个坐标系中的转化过程。
在计算机视觉中常采用右手定则来上图中的坐标系。图中存在三个不同层次的坐标系,以下是对这三种坐标系的定义。
(1)世界坐标系(Xw,Yw,Zw):就是现实坐标系或全局坐标系,它是客观世界的绝对坐标,是由用户任意定义的三维空间坐标系,一般的3D场景用的就是这种坐标系(HALCON标定中以标定板为参考坐标系基准)。
(2)相机坐标系(Xc,Yc):是以小孔相机模型针孔平面上的聚焦中心为原点,以相机光轴为Z。构成的三维坐标系,其中Xc、Yc与图像成像坐标系平行。
(3)图像坐标系:分为图像成像坐标系和图像像素坐标系。
图像成像坐标系(x,y) :其原点为透镜光轴与成像平面的交点,x、y轴分别平行于相机坐标系Xc轴和Yc轴,是平面直角坐标系,单位mm。
图像像素坐标系(u,v):是固定在图像上的以像素为单位的平面直角坐标系,其原点位于图像左上角,其横纵两轴(对于数字图像是行和列)分别平行于图像成像坐标系的横、纵坐标轴x、y,这也是HALCON中表示图像坐标系的方法。
二、坐标系的转换
下图是将相机平面移至针孔与目标物体之间以后的模型示意图,描述的是在这个移动过程中,成像平面上的投影点(点q)的变化情况。
将相机平面移至针孔与目标物体之间后的模型根据空间一点成像到图像平面上的路线,先由世界坐标系变换到相机坐标系,然后又由相机坐标系变换到图像成像坐标系,但是这个过程有畸变,需要进行变换处理,再由图像成像坐标系变换到图像像素坐标系,中间大致分为以下几个步骤。
1)从世界坐标系到相机坐标系
空间点Pw(Xw,Yw,Zw)转换到点P(Xc,Yc, Zc):
P=RPw+T (R是旋转矩阵,T是平移矩阵)
每一个世界坐标系的对象都可以通过旋转和平移变换到相机坐标系上。将目标点旋转θ角度,等价于将坐标系按相反的方向旋转θ角度。
对于三维坐标而言,旋转中绕某一个轴旋转,原理与二维坐标旋转相同。
如果将世界坐标系分别绕X、Y、Z轴旋转α、β、γ,那么,旋转矩阵分别为R(α)、R(β)、R(γ)。
总的旋转矩阵也就是三者的乘积:R(α,β,γ)=R(α)R(β)R(γ)
平移矩阵T=(tx,ty,tz),tx、ty、tz世界坐标系原点与相机坐标系目标点之间的差值。
2)从相机坐标系到图像坐标系(透视投影变换关系 即3D→2D)
有相似三角形可推出→x=fXc/Zc , y=fYc/Zc
此时投影点p的单位还是mm,并不是pixel(像素),需要进一步转换到像素坐标系。
3)从图像成像坐标系到图像像素坐标系
图像坐标系是一个二维坐标系,又分为图像像素坐标系和图像成像坐标系。图像像素坐标系u-v是以图像左上角为原点,以图像互为直角的两个边缘为坐标轴,满足右手准则而建立的。图像由一个个小的像素点组成,图像像素坐标系的横纵坐标正是以像素点为单位,用来描述图像中每一个像素点在图像中的位置。图像成像坐标系以光轴与像平面交点为原点建立,图像成像坐标系的两个坐标轴分别与图像像素坐标系的坐标轴平行,并且方向相同。
如图图像成像坐标系是以毫米为单位的直角坐标系x-y,用(u,v)来描述图像像素坐标系中的点,用(x,y)来描述图像成像坐标系中的点。图像成像坐标系的原点O在图像像素坐标系中的坐标为(Cx,Cy),用dx、dy来表示相邻像素点中心在x轴方向和y轴方向的实际物理距离,则与图像像素坐标系的转化关系为:
u=x/dx+Cx ; v=y/dy+Cy
标定的内外参数
一、外部参数
由前面可知,相机的外部参数用来描述相机坐标系与世界坐标系的关系,它表明相机在世界坐标系中的位置和方位,可用旋转矩阵和平移向量来表示。实质上旋转矩阵只有三个独立参数,加上平移向量的三个参数,故一共有六个独立的外部参数。
二、内部参数
内部参数只与相机内部结构有关,而与相机位置参数无关。主要包括图像主点坐标(Cx,Cy)(成像平面与相机光轴相交的点),单个像元的高、宽Sx、Sy,相机的有效焦距f和透视镜的畸变失真系数k等。
相机的内部参数有时也可以从制造商提供的说明书中查到,但是其精确性不能满足要求,仅可作为参考。在实际应用中还需要对它们进行进一步标定。主点坐标(Cx,Cy)理论上位于图像中心处,但实际上由于相机制作的精度和使用过程中相机镜头可以转动和拆卸等原因,使得面阵相机并不能保证其中心为透管光轴,且图像采集数字化窗口的中心不二定与光学中心重合,这就使得主点不一定在图像的中心,故而需要标定。单个像元的高、宽Sx、Sy,可以在制造商提供的技术文档中查到,但是该数据不是完全准确的。单个像元的高、宽理论上应该是相等的,但是由于制造的误差,两者不可能完全相等,因此需要根据实际情况对其进行修正。只有理想的透镜成像才满足透镜畸变失真系数的线性关系,实际上透镜存在多种非线性畸变,需要根据实际情况对它们进行修正。
Halcon标定流程
标定步骤
标定前需要生成一个.descr的描述文件,也就是世界坐标系与像素坐标系的关系,当我们下一次做别的项目时,只需要调用描述文件,即可完成标定过程。
在使用标定助手的一些注意事项:
(1)标定板材质选用玻璃或者陶瓷材质为最好。
(2)光源尽量在标定板前方,在与相机相反的方向。
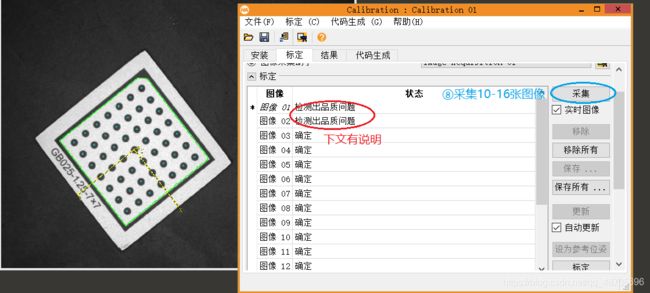
(3)标定板采集图像尽量在12幅以上,数量越多,所得的参数就越精确。
(4)为了保证参数的精确性,要保证标定板的四角全部在视野范围内。这样做主要是因为一般标定板的四角畸变量比较大,需要通过四角的畸变程度获得准确的畸变系数。
(5)要保证标定板的标志点灰度值与其背景灰度值的差值在100以上,否则HALOCN会提示有品质问题。
标定板
这里我用的标定板是7*7圆点标定板,型号:HC070—3.75
![]()
标定板数据可参考:
![]()
另外推荐师兄的一篇关于标定的博客:
[Halcon&标定] 单相机标定_halcon相机标定_丶布布的博客-CSDN博客[Halcon&标定] 单相机标定_halcon相机标定_丶布布的博客-CSDN博客[Halcon&标定] 单相机标定_halcon相机标定_丶布布的博客-CSDN博客
转自:(2条消息) Halcon_标定_halcon标定_x1angzeeD.的博客-CSDN博客