BP神经网络应用案例

目录

背景介绍

【神经网络符号说明】

 【建立网络拓扑结构】

【神经网络学习步骤】

步骤1 准备输入和输出样本

步骤2  确定网络学习参数

 步骤3  初始化网络权值W和阀值B

 步骤4  计算网络第一层的输入和输出

步骤5 计算中间层（隐含层输入和输出）

步骤6 计算输出层的输入和输出​编辑

步骤7 计算能量函数

步骤8 计算能量函数对各参数的偏导数（梯度）

步骤9 计算各权值的调整量

步骤10  调整各个权值

步骤11 网络输出的还原

 神经网络训练（建模过程的有关细节略去）

输入变量

输出变量

【基于案例的网络训练效果与参数的关系】

1、其余要素不变，训练次数与误差的关系

 2、隐含层神经元数量与误差关系

3、学习效率与误差关系

 4、利用训练好的网络进行预测

 5、避免过度拟合，需要对样本输出做干扰处理

---

背景介绍

冶金技术，钢铁开始锻炼的“开始温度”与13个指标有关，见表(1)。

出钢时间/h	钢水净重量/t	吹止温度/oC	高碳锰铁/t	低碳锰铁/t	硅锰铁/t	硅铁/t	铝块/t	增碳剂/t	中碳锰铁/t	包龄/炉/包	运输时间/min	等待时间/min	开始温度
3	279000	1673	0	5211	0	0	667	0	0	14	45.78	3.03	1557
6	274000	1669	0	5116	0	0	501	0	0	56	9.23	9.37	1561
6	280000	1675	0	5050	0	0	497	0	0	77	22.42	8.83	1583
9	267000	1650	0	5032	0	0	0	0	0	62	24.03	7.17	1553
6	280000	1657	0	4655	0	0	498	0	0	19	28.52	12.3	1574
7	303000	1659	0	1124	0	0	413	180	0	12	45.6	8.13	1568
7	283000	1655	0	1112	0	0	447	176	0	84	46.18	8	1576
7	280000	1649	0	1110	0	0	459	281	0	75	25.07	8.63	1575
5	278000	1641	9876	0	0	2996	2604	472	0	13	30.55	10.27	1594
6	285000	1659	2531	0	0	696	466	73	0	58	19.67	7.87	1570
9	279737	1652	2326	0	0	702	413	64	0	11	33.93	7.07	1550
9	279195	1658	2295	0	0	641	403	94	0	33	40.3	6.97	1566
5	274000	1666	2208	0	0	747	404	103	0	8	25.45	11.8	1578
6	280201	1671	2015	0	0	356	450	0	806	48	28.7	2.83	1591
6	275000	1689	2011	0	0	512	566	0	1597	72	31.63	10.73	1585
5	273000	1647	2003	0	0	603	415	0	0	26	21.4	8.78	1574
8	295000	1633	1806	0	2032	307	305	0	800	16	27.02	10.92	1563
6	276000	1646	1501	0	0	247	446	0	445	86	35.88	11.9	1532
7	292000	1668	1295	0	3786	82	300	50	0	98	24.95	10.43	1563
5	290000	1670	996	0	3507	0	449	0	151	5	45.55	9.72	1572
6	293000	1687	203	0	0	700	296	154	0	59	37.68	8.53	1592
6	288000	1659	0	0	2282	302	449	0	1005	15	25.5	11.45	1575
3	290762	1671	0	0	2046	105	484	0	2715	39	45.3	2.83	1571
6	280875	1658	0	0	2195	0	399	0	2452	7	23.27	7.03	1597
8	284000	1625	0	0	2049	0	467	0	2714	59	34.65	8.2	1595
7	284000	1661	0	0	2018	0	463	0	2649	56	19.13	11.17	1569
6	280000	1669	0	0	2010	0	397	0	2582	13	16.2	9.13	1598
8	257000	1662	0	0	2008	0	422	0	2492	55	10.8	9.03	1606
7	274660	1675	0	0	1503	0	523	0	3326	55	11.22	10.87	1593
6	266000	1673	0	0	1362	0	621	0	3299	61	11.33	9.33	1598

                                                表1 钢铁锻炼的有关指标 

 由冶金机理可知，钢铁开始锻炼的“开始温度”（表中最后1列）会受到出钢时间、钢水净重、吹止温度、高碳锰铁、…、等待时间等13个因素（表1中前13列）影响。这里，将前13列作为输入因子，最后一列作为输出因子，用于学习如何训练BP神经网络及其步骤。

【神经网络符号说明】

• 系统X输入样本；Y系统输出样本；
• I1 输入层输入数据；O1为输入层输出数据;
• I2 隐含层输入数据；O2为隐含层输出数据；
• I3 输出层输入数据；O3输出层输出数据;
• 输入层和输出层采用线性函数f(x)=x;
• 隐含层采用S型刺激函数(第1个，0到1);
• W1为输入层到隐含层权值，B1为输入层到隐含层阀值；
• W2为隐含层到输出层权值，B2为隐含层到输出层阀值；
• E=Ones 为元素为1的行矩阵，维数与Y一致;

 【建立网络拓扑结构】

 针对本案例，需要说明：（1）输入层输入I1=X13×30;（2）由输入层到隐含层参数(W1)12×13,(B1)12×1;（3）中间层到输出层(W2)1×12,(B2)1×1;（4）为了满足矩阵相加,(E)1×30. 

【神经网络学习步骤】

步骤1 准备输入和输出样本

设X为13行30列的输入样本矩阵，Y为1行30列的输出样本。由于输入和输出矩阵的数据量纲不同，计量单位也不同，需要归一化，有两种方式

 

or

步骤2  确定网络学习参数

最大训练次数   5000
隐含层神经元数量（或隐含层数量，各层神经元数量）
               1层，12个神经元
网络学习效率（速度）   0.035
训练目标误差     0.65×10-3.
是否添加动量因子    否

 步骤3  初始化网络权值W和阀值B

W1和B1，W2和B2都采用随机数生成。另外特别说明:

1. 训练步骤是按照批量形式进行（即样本一次全部输入，采用矩阵运算）
2. 阀值写成权值形式，也就是说阀值看成样本输入为1的随机数
3. 数据输入是按照行作为一个输入维度（不是列），即每个样本为一个输入维度，即X的形式要把握

 步骤4  计算网络第一层的输入和输出

由于样本输入就是第一层输入，第一层输入又是线性函数，所以有

步骤5 计算中间层（隐含层输入和输出）

步骤6 计算输出层的输入和输出

步骤7 计算能量函数

记为残差向量，能量函数定义为

步骤8 计算能量函数对各参数的偏导数（梯度）

（1）把能量函数写成所有权系数的逐步复合函数，求能量函数关于这些权系数的偏导数（表达成梯度向量）

（2）计算能量函数对权的偏导数 根据复合函数求导链式法则，有

 注意：点乘·表示两个矩阵对应分量相乘得到同型矩阵。

步骤9 计算各权值的调整量

由于负梯度方向是能量函数下降最快的方向，故各个权系数的调整量为

其中，表示学习效率（速度，也就是搜索步长）。

步骤10  调整各个权值

权值=权值+调整量，先调整输出层到隐含层的权值，再调整隐含层到输入层的权值。这个调整方向和计算网络输出的方向刚好相反，故称为前向反馈网络。 

 由于负梯度方向搜索法容易限于局部极值，故很多问题里，调整量还附加了动量因子。

步骤11 网络输出的还原

根据步骤1数据归一化的逆函数，将网络输出还原为样本输出等同意义的数据，用于决策。

{(0,1)还原}

{（-1，1）还原}

在神经网络学习术语里，称样本输出Y为导师数据，或监督数据，称有参考数据的网络学习为有监督学习或有导师学习。而在没有给出监督数据的问题里，要根据问题，构造一个理想的(不存在的)的监督数据，以确定能量函数。现代机器学习人工智能深度学习的一个困惑或难点就是确定合理的导师数据。从上面11步骤可以看到，神经网络训练其实就是利用最小二乘法求解合适的权系数（用的是逆向反馈法）。

 神经网络训练（建模过程的有关细节略去）

 案例数据存放地点：

A=xlsread('d:\ganglengque.xlsx');
X=A(:,1:end-1)';Y=A(:,end)';

编写一个负梯度训练子程序

function [W1,W2,B1,B2,eb,s2]=BPnn(X,Y,n1,n,lr,sig)
[X]=mapminmax(X);
[Y,s2]=mapminmax(Y);
W1=rand(n1,13);B1=rand(n1,1);
W2=rand(1,n1);B2=rand(1,1);
E=ones(size(Y));
eb=[];
for i=1:n
    I1=X;
    O1=I1;
    I2=W1*O1+B1*E;
    O2=logsig(I2);
    I3=W2*O2+B2*E;
    O3=I3;
    err=Y-O3;
    hrr=sum(err.^2)^0.5;
    eb=[eb,hrr];
    if hrr

输入变量

 样本输入X；样本输出Y；隐含层神经元n1;训练次数n;学习效率lr；误差容许sig；

输出变量

 按要求训练得到的权系数W1,W2,B1,B2；各次训练残差痕迹向量eb；输出样本归一化信息s2.

【基于案例的网络训练效果与参数的关系】

1、其余要素不变，训练次数与误差的关系

将训练后的网络输出与样本输出（都归一化）绘制散点图，可以看出拟合好坏（即误差直观体现）

A=xlsread('d:\ganglengque.xlsx');
X=A(:,1:end-1)';Y=A(:,end)';
n1=12;lr=0.035;sig=0.003;
[W1,W2,B1,B2,eb,s2]=BPnn(X,Y,n1,20,lr,sig);
[W1,W2,B1,B2,eb,s2]=BPnn(X,Y,n1,60,lr,sig);
[W1,W2,B1,B2,eb,s2]=BPnn(X,Y,n1,180,lr,sig);
[W1,W2,B1,B2,eb,s2]=BPnn(X,Y,n1,500,lr,sig);
[W1,W2,B1,B2,eb,s2]=BPnn(X,Y,n1,1000,lr,sig);
[W1,W2,B1,B2,eb,s2]=BPnn(X,Y,n1,2000,lr,sig);

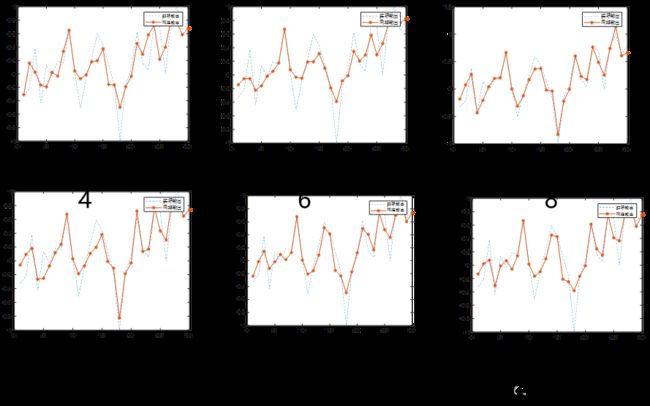
 2、隐含层神经元数量与误差关系

其它要素不变，都训练500次，隐含层神经元n1分别取4,6，8,10,12,16，观察拟合效果曲线

A=xlsread('d:\ganglengque.xlsx');
X=A(:,1:end-1)';Y=A(:,end)';
n=1000,lr=0.035;sig=0.003;
[W1,W2,B1,B2,eb,s2]=BPnn(X,Y,4,n,lr,sig);
[W1,W2,B1,B2,eb,s2]=BPnn(X,Y,6,n,lr,sig);
[W1,W2,B1,B2,eb,s2]=BPnn(X,Y,8,n,lr,sig);
[W1,W2,B1,B2,eb,s2]=BPnn(X,Y,10,n,lr,sig);
[W1,W2,B1,B2,eb,s2]=BPnn(X,Y,12,n,lr,sig);
[W1,W2,B1,B2,eb,s2]=BPnn(X,Y,16,n,lr,sig);

3、学习效率与误差关系

它输入因素不变，训练次数n=500,隐含层神经元n1=12,让学习效率lr分别取0.1，0.05，0.02，0.01，0.005，0.001，观察拟合曲线的效果

 4、利用训练好的网络进行预测

对n1=12,n=4000,lr=0.035，案例1提供的训练样本，输出训练好的权系数。如图所示，训练效果很好。

A=xlsread('d:\ganglengque.xlsx');
X=A(:,1:end-1)';Y=A(:,end)';
n=4000;n1=12;sig=0.003;lr=0.035;
[W1,W2,B1,B2,eb,s2]=BPnn(X,Y,n1,n,lr,sig);

训练完成的权系数W1,W2,B1,B2保存在表2中，用不同颜色区分。

W1=	1	2	3	4	5	6	7	8	9	10	11	12	13	B1=
1	0.05	-0.84	0.97	0.96	0.18	0.20	0.85	0.00	0.80	1.30	-0.37	0.23	0.76	0.28
2	-0.65	1.74	0.41	-0.37	-0.41	0.60	0.65	0.38	0.48	1.63	1.55	1.83	0.35	0.46
3	0.57	0.86	0.79	0.45	1.55	0.17	0.67	0.78	0.24	0.27	0.90	1.07	0.66	-0.17
4	0.30	0.00	0.32	1.05	0.22	0.25	0.74	0.75	0.77	0.63	0.52	0.24	-0.09	0.45
5	0.23	0.08	0.76	0.85	-0.69	1.48	0.26	0.55	0.48	1.80	-0.03	0.00	-0.67	0.40
6	1.79	-0.87	-1.57	0.92	0.50	2.29	0.36	0.33	0.79	0.94	0.02	0.93	-0.35	0.07
7	0.30	0.35	0.71	1.04	0.45	0.11	0.80	0.89	0.89	0.60	0.26	0.40	0.59	0.14
8	3.15	0.16	-0.38	1.66	-0.33	-0.60	1.83	0.62	-0.48	-0.38	1.57	0.10	1.67	-0.52
9	-0.33	-0.22	0.64	0.87	1.70	-0.21	0.24	0.83	0.18	0.39	0.47	-0.15	-0.55	0.03
10	0.52	0.70	0.12	0.61	0.82	0.74	0.94	1.12	1.01	0.32	0.31	0.38	0.48	0.55
11	0.90	0.70	0.71	0.85	1.00	0.66	0.29	0.50	1.07	0.79	0.34	0.54	0.32	0.11
12	1.12	0.28	2.61	1.13	0.00	-0.72	1.32	0.69	1.08	-0.18	2.17	1.17	-0.25	0.63
W2=	0.82	-1.11	0.80	-0.03	0.95	1.88	-0.15	-1.62	-1.12	-0.06	-0.05	1.38	B2= 0.16

 5、避免过度拟合，需要对样本输出做干扰处理

对网络输入（已经归一化后的数据），在添加一个噪声向量，即Y=Y+noise，一般noise为均值为0的正态分布 ，即noise=normrnd(0,1,size(Y);         Y=Y+r*noise;

r为噪声强度，一般r非常小。

取r=0.01，加入BP神经网络拟合中，代码如下

function [W1,W2,B1,B2,eb,s2]=BPnnn(X,Y,n1,n,lr,sig)
[X]=mapminmax(X);
[Y,s2]=mapminmax(Y);
noise=normrnd(0,1,size(Y));
Y=Y+0.2*noise;
W1=rand(n1,13);B1=rand(n1,1);
W2=rand(1,n1);B2=rand(1,1);
E=ones(size(Y));
eb=[];
for i=1:n
    I1=X;
    O1=I1;
    I2=W1*O1+B1*E;
    O2=logsig(I2);
    I3=W2*O2+B2*E;
    O3=I3;
    err=Y-O3;
    hrr=sum(err.^2)^0.5;
    eb=[eb,hrr];
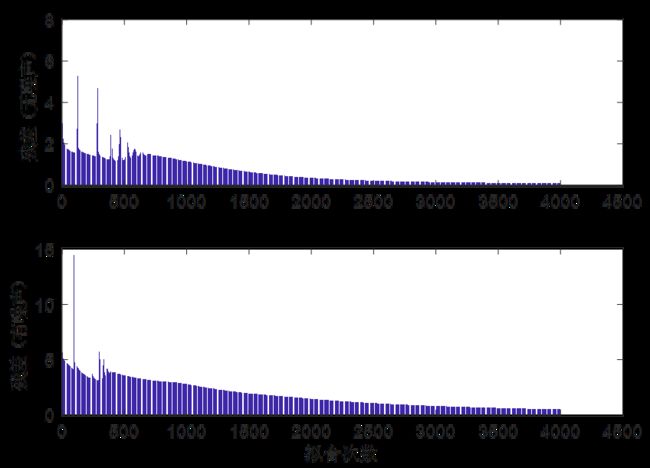
    if hrr

在隐含层神经元n1=12,学习效率lr=0.035，训练次数n=4000情况下，容差sig=0.003情况下，将有噪声（强度系数0.8）和无噪声两种情况的残差结果进行对比，见下图。可以看出，有噪声收敛速度慢于无噪声。

A=xlsread('d:\ganglengque.xlsx');
X=A(:,1:end-1)';Y=A(:,end)';
n1=12;lr=0.035;sig=0.003;n=4000;
[W1,W2,B1,B2,eb1,s1]=BPnn(X,Y,n1,n,lr,sig);
[W11,W21,B11,B21,eb2,s2]=BPnnn(X,Y,n1,n,lr,sig);
subplot(2,1,1);
bar(eb1);
subplot(2,1,2);
bar(eb2);