【算法篇】八种内排序算法
常用的八种内排序算法分别是:
- 交换排序:冒泡排序、快速排序
- 选择排序:简单选择排序、堆排序
- 插入排序:直接插入排序、希尔排序
- 归并排序
- 基数排序
内排序巧记:选(选择)舰(简单选择)队(堆)的时候脚(交换)毛(冒泡)快(快速),需要把轨(归并)迹(基数)擦(插入)仔(直接插入)细(希尔)
一、算法的概念和编码实现(Java)
1、冒泡排序
冒泡排序的基本思想是,对相邻的元素进行两两比较,顺序相反则进行交换,这样,每一趟会将最小或最大的元素“浮”到顶端,最终达到完全有序
代码实现(升序)
public static void selectSort(int[] array) {
int len = array.length;
boolean flag = true;
for (int i = 0; i < len - 1 && flag; i++) {
flag = false;
for (int j = 0; j < len - i - 1; j++) {
if (array[j] > array[j + 1]) {
int temp = array[j];
array[j] = array[j + 1];
array[j + 1] = temp;
flag = true;
}
}
}
}| 最好情况的时间复杂度 | 最坏情况的时间复杂度 | 特点 | 稳定性 |
|---|---|---|---|
| T(n)=O(n) | T(n)=O(n2) | 如果数据已经排序好,一次都不交换或者交换次数很少,效率很高;如果是完全逆序,则要不停的两两交换,效率很低 | 稳定 |
2、简单选择排序
简单选择排序的基本思想是,每一趟从待排序的数据元素中选择一个最小(或者最大)的元素作为首元素,直到所有元素排完为止。
代码实现(升序):
public static void selectSort(int[] array) {
int len = array.length;
for (int i = 0; i < len-1; i++) {
int min = i;// 每趟排序默认第一个元素是最小的元素,记住下标
for (int j = i + 1; j < len; j++) {
// 从i+1的位置开始,依次同最小元素比较,若比最小元素小,则记住当前下标
if (array[j] < array[min]) {
min = j;
}
}
// 无序区最小元素同无序区的第一个元素交换
if (min != i) {
int temp = array[min];
array[min] = array[i];
array[i] = temp;
}
}
}| 时间复杂度 | 特点 | 稳定性 |
|---|---|---|
| T(n)=O(n2) | 简单,相对于冒泡排序来说交换次数少 | 不稳定 |
3、直接插入排序
直接插入排序基本思想是不断将无序区的元素插入到有序区的适当位置,直到无序区没有元素排完为止
代码实现(升序):
private static void insertSort(int[] array) {
for (int i = 1; i < array.length; i++) {
int j ;
int temp = array[i];
for (j = i; j>0 && temp < array[j-1]; j--) {
array[j] = array[j-1];
}
array[j] = temp;
}
}| 最好情况的时间复杂度 | 最坏情况的时间复杂度 | 特点 | 稳定性 |
|---|---|---|---|
| T(n)=O(n) | T(n)=O(n2) | 简单 | 稳定 |
4、快速排序
对冒泡排序的一种改进,它的思想是:将元素分为两组,一组的元素比另外一组的所有元素都要小,然后再按照此方法对两组元素进行排序。
快速排序我这里就不写了,快速排序相对于前面三种排序方式来说要复杂很多,看了一些博客,发现写得都不怎么样,这里推荐一个讲快速排序的视频java快速排序讲解_哔哩哔哩_bilibili
附上代码实现(参考视频中的):
public static void quickSort(int[] arr,int left,int right){
//如果左边索引比右边索引更大或者相等,直接使用return结束这个方法
if(left >= right){
return;
}
//定义变量保存基准数
int base = arr[left];
//定义变量i,指向最左边
int i = left;
//定义变量j,指向最右边
int j = right;
//当i和j不相遇的时候,在循环中进行检索
while(i!=j){
//先由j从右向左检索比基准数小的就停下,否则继续检索
while(arr[j]>=base && i| 最好情况的时间复杂度 | 最坏情况的时间复杂度 | 平均时间复杂度 | 特点 | 稳定性 |
|---|---|---|---|---|
| T(n)=O(nlogn) | T(n)=O(n2) | T(n)=O(nlogn) | 较复杂 | 不稳定 |
如何计算快排的时间复杂度以及快排的改进快速排序时间复杂度分析 - 知乎
C语言算法:程序7.3 - 非递归快速排序_哔哩哔哩_bilibili
5、希尔排序
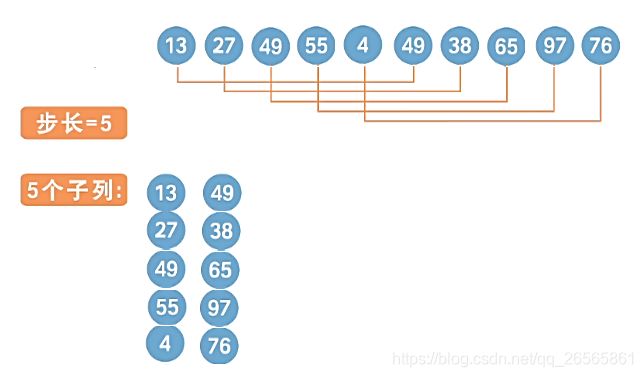
希尔排序是对直接插入排序的优化,原理是:将数据按照步长dk分为dk个子列,然后再对每个子列运用直接插入排序。
当步长为5的时候,分组情况如下:
每个子列排好序后,变成:
代码实现(升序):
public static void main(String[] args) {
int[] array = {49,38,65,97,76,13,27,49,55,4};
print(array);
ShellSort(array,5);
print(array);
ShellSort(array,3);
print(array);
ShellSort(array,1);
print(array);
}
private static void print(int[] array){
for (int i = 0; i < array.length; i++) {
System.out.print(array[i]+"\t");
}
System.out.println("\n");
}
//希尔排序,dk表示步长
private static void ShellSort(int[] array,int dk) {
for(int k = 0;k=0 && temp < array[j-dk]; ) {
j -= dk;//上一个元素的索引需要减去dk,而不是减1
array[j] = array[j-dk];
}
array[j] = temp;
i += dk;//下一个元素索引加上dk,而不是加1
}
}
} 说明:从代码层面来看,希尔排序相对于直接插入排序的不同点在于希尔排序外层多了一层循环,用来将原序列分层若干个子列。内部的直接插入排序做减减或者加加时要改成减去步长或者加上步长
二、时间复杂度和空间复杂度分析
排序的稳定性:根据关键字相同(如果数值比较的话是指大小)的记录排序前后相对位置的变化,可以分为稳定性排序算法和不稳定性排序算法。在排序的序列中,如果存在两个记录Ri和Rj,其关键字分别为Ki和Kj,并且i<=j,Ki=Kj,即记录Ri在Rj之前,排序完成后,如果记录Ri和Rj的相对位置不发生改变,那么该算法是稳定性排序,否则是不稳定排序。
| 排序方法 | 时间复杂度(最坏情况) | 空间复杂度(辅助空间) | 稳定性 | 复杂性 |
| 简单选择排序 | O(n2) | O(1) | 不稳定 | 简单 |
| 冒泡排序 | O(n2) | O(1) | 稳定 | 简单 |
| 快速排序 | O(n2) | 不稳定 | 较复杂 | |
| 直接插入排序 | O(n2) | O(1) | 稳定 | 简单 |
| 希尔排序 | O(n2) | O(1) | 不稳定 | 较复杂 |