acwing数据结构笔记（一）

前言：书读百遍其义自见，代码也是一样，不断地写不断地背，才能熟练的掌握
y总：yxc
链接：https://www.acwing.com/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

一、链表与邻接表

说明：这种方式new Node（）非常慢。当然，这是针对算法竞赛笔试，只考虑时间最优。考研还是用这种的。
y总讲的是用数组来模拟单链表和双链表。原因就是比new快。

（1）单链表

• 构建链表

const int N = 100010;
int head, e[N], ne[N], idx;

如何理解idx呢？

idx相当于新开的元素的地址，或者理解成新开结点的个数

• 初始化

void init()
{
	head = -1;
	idx = 0;
}

• 将x插入到头结点（头指针指向的结点）

void add_to_head ()
{
	e[idx] = x, ne[idx] = head, head = idx, idx ++
}

• 将x插入到下标是k的元素后面

void add(int k, int x)
{
	e[idx] = x;				//给当前结点赋值
	ne[idx] = ne[k];		//将下标为k的next指针给当前结点
	ne[k] = idx;			//将下标为k的元素指向当前结点
	idx ++;
}

• 删掉下标为k的后面一个结点(k指针直接指向下下个）

void remove()
{
	ne[k] = ne[ne[k]];
}

（2）双链表

• 构建双链表

const int N = 10010;
int e[N], l[N], r[N], idx;

• 初始化

void init ()
{
	//偷个懒，假设0是左端点，1是右端点
	r[0] = 1;
	l[1] = 0;
	idx = 2;
}	

• 在下标为k的右边插入x

void add(int k, int x)
{
	e[idx] = x;
	r[idx] = r[k];
	l[idx] = k;
	l[r[k]] = idx;
	r[k] = idx;
}

• 删除下标为k的元素

void remove(int k)
{
	r[l[k]] = r[k];
	l[r[k]] = l[k];
}

二、栈与队列

（1）基本定义
栈：先进后出
队列：先进先出

（2）用数组模拟栈
栈的操作很简单，所以不需要额外定义函数。

• 构建栈

int stk[N], tt;		//stk是stack，栈的意思；tt是top，栈顶的意思

• 输入栈顶元素(push)

stk[ ++ tt] = x;

• 弹出栈顶元素(pop)

tt --;

• 判断非空

if (tt)  not empty
else empty

• 查询栈顶元素

cout << stk[tt] << endl;

（3）单调栈
1.题目描述：给定一个长度为 N 的整数数列，输出每个数左边第一个比它小的数，如果不存在则输出 −1。
2.思路： 找出左边第一个比它小，意味着最终这是一个向右单调递增的栈，故名单调栈。
在保持栈内元素单调的情况下，如果新元素x比栈顶元素小，说明后面入栈的数找到第一个比它小的数一定是这个x而不是x前面的大数，因此x会将前面所有比它大的元素全部弹出。
3.时间复杂度： O（n）
4.【算法模板】

#include 
using namespace std;
const int N = 100010;
int stk[N], tt;

int main()
{
    int n;
    cin >> n;
    while (n -- )
    {
        int x;
        scanf("%d", &x);
        while (tt && stk[tt] >= x) tt -- ;	//tt非空且栈顶大于x，则弹出栈顶元素
        if (!tt) printf("-1 ");				//若栈为空，则输出 - 1
        else printf("%d ", stk[tt]);	//若栈非空，则输出上一个值（第一个比它小的）
        stk[ ++ tt] = x;				//将输入的值放进栈里，注意tt从0开始计数
    }
    return 0;
}

（4）KMP算法

①子串的定位运算通常称为串的模式匹配或串匹配。广泛用于拼写检查、数据压缩等应用中。
②串的模式匹配设有主串S（也称正文串）和子串T（模式），在主串S中查找与模式T相匹配的子串，若匹配成功，则返回子串第一个字符在主串S中的下标

1.BF算法介绍

这是最朴素的算法：依次比较主串 i 和子串 j 所指的字符，若不匹配，则i指针回溯到 i - j + 2处重新进行匹配。在最坏情况下平均时间复杂度为O(n x m)，因此改进为kmp算法

2.kmp算法介绍

KMP可以在O(n + m)的时间数量级完成匹配操作。其改进在于：不需回溯 i 指针，利用“已匹配”的结果将子串向右滑动尽可能远的一段距离。

注意点：一般next[ j ]开头都是 0 1，注意 J从1开始取，比较的是k - 1个元素。

（1）KMP算法
【算法步骤】

（2）求next值
【算法步骤】

（3）求next的修正值nextval
【算法步骤】

三、Trie树

一种可以快速存储和查找字符串、二进制数集合的数据结构

此图用来表示存储方式，五角星表示以该字符为结尾的“单词”存在。

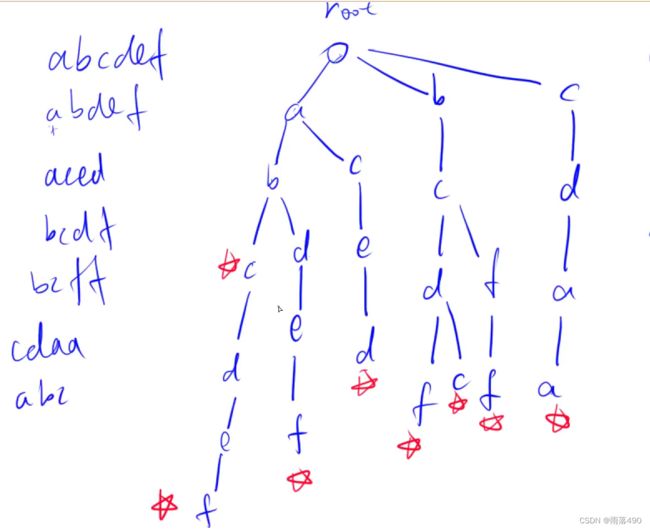
（1）用数组模拟指针
下标：idx——>第x个数
儿子：son[x][0] ——>x代表结点x，0代表这是x的第0个儿子，即 ‘a’
计数：cnt[x] ——>以x结尾的单词有多少个
维护：idx ——>用来记录每个结点的编号

（2）基本操作

• 初始化

const int N  = 100010;
int son[N][M], idx;		
//N表示trie树结点个数，M表示每个结点的儿子个数，idx是第idx个结点

• 插入

void insert(char *str)
{
    int p = 0;								//令p等于根节点
    for (int i = 0; str[i]; i ++ )			//从根节点开始向下遍历
    {
        int u = str[i] - 'a';				//输入结点儿子的值
        if (!son[p][u]) son[p][u] = ++ idx; //若不存在儿子，则创建一个儿子
        p = son[p][u];						//指针指向新儿子
    }
    cnt[p] ++ ;
}

• 查询

int query(char *str)
{
    int p = 0;
    for (int i = 0; str[i]; i ++ )
    {
        int u = str[i] - 'a';
        if (!son[p][u]) return 0;
        p = son[p][u];
    }
    return cnt[p];
}

四、并查集

（1）基本使用场景
①将两个集合合并
②询问两个元素是否在一个集合当中

（2）基本原理
每个集合用一棵树来表示。树根的编号就是整个集合的编号。每个结点用p[x]结点用来表示存储他的父节点

（3）问题处理
①如何判断树根： if(p[x] == x)
②如何求x的集合编号: while(p[x] !=x) x = p[x];
③如何合并两个集合: px是x的集合编号，py是y的集合编号。p[x] = y

这里注意：在处理第二步的时候有一个优化：路径压缩。这节内容记住这个优化模板就行。

【算法描述】

#include 
using namespace std;
const int N = 100010;

int n, m;
int p[N];   //一定要定义一个father数组，用来存储每个数的父亲结点

int find (int x)    //核心步骤：返回x的祖宗结点 + 路径压缩
{
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i ++) p[i] = i;     //初始状态每个数都在自己的集合当中，所以父结点就是自己
    
    while (m --)
    {
        char op[2];
        int a, b;
        scanf("%s%d%d", op, &a, &b);
        if (*op == 'M') p[find(a)] = find(b);   //让a的祖宗结点连接在b的祖宗结点下面
        else
        {
            if (find(a) == find(b)) puts("Yes");
            else puts("No");
        }
    }
    return 0;
}

五、堆（Heap）

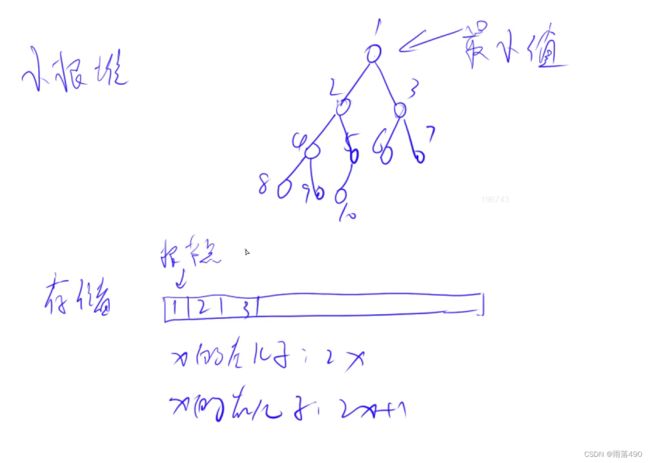
定义：堆又可称之为完全二叉堆。这是一个逻辑上基于完全二叉树、物理上一般基于线性数据结构（如数组、向量、链表等）的一种数据结构。

（一）堆的存储

• 小根堆
  ①根节点的值最小 ②堆可以用一维数组保存。假设根的坐标为x，则左儿子为2x，右儿子为2x + 1 ③下标从1开始比较方便，因为如果是0的话2x还是0。
  

（二）堆的基本操作
1.插入一个数

heap[ ++ size] = x; up(size);

2.求集合当中的最小值

heap[1];

3.删除最小值

heap [1] = heap[size]; size --; down(1);	//替代，干掉，下沉

4.删除任意一个元素

heap[k] = heap[size]; size--; down(k);up(k);	//不知道上升还是下沉干脆都做一遍好了

5.修改任意一个元素

heap[k] = x; down(k); up(k);

6.down操作：使权数大的值下沉（对大根堆就是使权数小的值下沉）

void down(int u)
{
	int t = u;		//假设t是三者中最小的
	if (u * 2 <= cnt && h[u * 2] < h[t]) t = u * 2;				//判断左儿子
	if (u * 2 + 1 <= cnt && h[u * 2 + 1] < h[t]) t = u * 2 + 1	//判断右儿子
	if (u != t)		//若最小的不是u，则u下沉
	{
		swap(h[u], h[t]);
		down (t);
	}
}

7.up操作

--------未更完--------

六、哈希表

散列表（Hash table，也叫哈希表），是根据关键码值(Key value)而直接进行访问的数据结构。也就是说，它通过把关键码值映射到表中一个位置来访问记录，以加快查找的速度。这个映射函数叫做哈希函数，存放记录的数组叫做哈希表。

（一）基本概念

• 使用场景：将一个较大的值域里的数映射到较小范围数中。
• 对不同关键字很有可能映射到同一哈希地址，这种现象称为“冲突”，根据解决冲突的方式可以分为“拉链法”和“开放寻址法”。
• （思维导图）
  
  （二）存储结构
  （1）拉链法-----一个单数组拉了很多链
• 图示
  

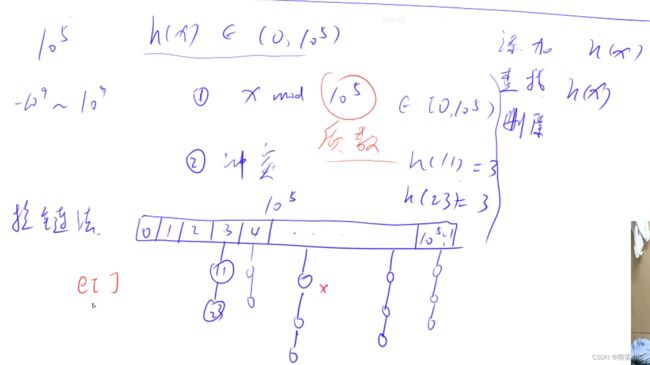
1、定义哈希数组，将原数组映射到哈希数组中。
2、哈希数组的范围N最好取质数
3、scanf输入字符串可以自动过滤空格或空字符

• 代码

int h[N], e[N], ne[N], idx;

    // 向哈希表中插入一个数
    void insert(int x)
    {
        int k = (x % N + N) % N;
        e[idx] = x;
        ne[idx] = h[k];
        h[k] = idx ++ ;
    }

    // 在哈希表中查询某个数是否存在
    bool find(int x)
    {
        int k = (x % N + N) % N;
        for (int i = h[k]; i != -1; i = ne[i])
            if (e[i] == x)
                return true;

        return false;
    }

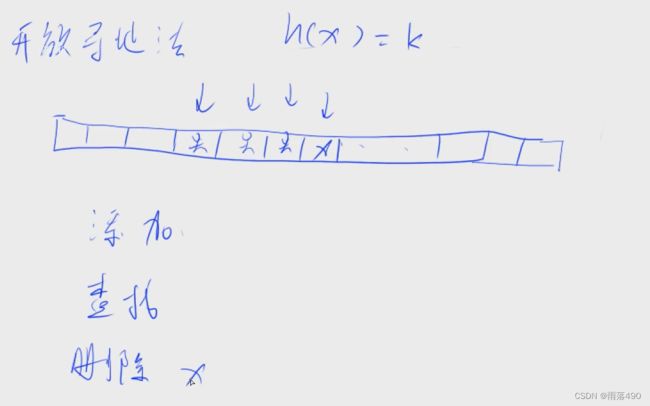
（2）开放寻址法（坑位？？）

• 图示
  
• 思路
  1.开一个2~3倍的哈希数组，保证映射后的数一定有位置存放
  2.循环整个数组，find函数返回可存放的位置。令h[find(x)] = x即可。
• 代码

#include 
#include 
using namespace std;
const int N = 200003, null = 0x3f3f3f3f;
int h[N];

int find(int x)
{
    int t = (x % N + N) % N;    //映射
    while (h[t] != null && h[t] != x)
    {
        t ++;
        if (t == N) t = 0;
    }
    return t;
}

int main()
{
    int n;
    scanf("%d", &n);
    memset(h, 0x3f, sizeof h);    
    while (n --)
    {
        char op[2];
        int x;
        scanf("%s%d", op, &x);
        
        if (*op == 'I') h[find(x)] = x;
        else
        {
            if (h[find(x)] == null) puts("No");
            else puts("Yes");
        }
    }
    return 0;
}

（三）字符串的哈希方式

1预处理全部前缀的哈希（吧字符串看成p进制数-> 转化为10进制数-> 模上较小的数Q）