【每天学习亿点点系列】——杨氏矩阵，字符串左旋，字符串旋转结果

题1.杨氏矩阵

有一个数字矩阵，矩阵的每行从左到右是递增的，矩阵从上到下是递增的，请编写程序在这样的矩阵中查找某个数字是否存在。
要求：时间复杂度小于O(n)

解决思路

下面是一个杨氏矩阵：

如果这一题没有时间复杂度的要求，那是很容易完成的，一个个遍历一下就行了。既然要满足时间复杂度的要求，那我们就要另辟蹊径。
题目中还给了一个条件别忘记了:矩阵的每行从左到右是递增的，矩阵从上到下是递增的。这个时候就自然而然的会想：是否可以利用这个条件排除掉一些数据，这样不就不需要每个都遍历一次了吗？

答案肯定是可以的，下面来看看具体的思路。

由于杨氏矩阵的特点决定了针对表中的任一元素，下方和右方的数据一定大于我，左方和上方的数据一定小于我，所以查找的时候可以利用这一特点，从右上或者左下角来找。因为这两个位置的大于小于是有区分度的。例如我选择从右上角找，那么没有上边和右边，所以下边一定比我大，左边一定比我小，那么要查找的数字如果比我大，那我就向下，如果比我小，那我就向左，这样查找的次数只有x+y-1次，符合题目中要求的O(n)。

上面的思路中可以看到我举的是右上角的例子，左下角其实也一样。下面来看一下实现的过程。

代码实现

int Find(int a[3][3],int x,int y, int n)
{
	int i = 0;
	int j = x-1;     //让他从右上角开始遍历
	while (j >= 0 && i < y)
	{
		if (a[i][j] < n)  //如果比n小，说明在下面，则i++
		{
				i++;
		}
		else if (a[i][j]>n) //如果比n大，说明在左边，则j--
		{
				j--; 
		}
		else   //不大也不小，正好找到
		{
				return 1;  
		}
	};
	return 0;
}
int main()
{
	int a[3][3] = { { 1, 3, 5 }
	              , { 3, 5, 7 },
	                { 5, 7, 9 } 
	               };
	int n = 0;
	printf("请输入你要寻找的数字\n");
	scanf("%d", &n);
	if (Find(a,3,3,n) == 1)
	{
		printf("Find\n");
	}
	else
	{
		printf("Not Find\n");
	}
	return 0;
}

题2.字符串左旋

解决思路

方法一：逐个左旋

设计循环使其可以旋1次，然后让他执行n次。

这是循环一次的效果。

代码实现

void leftRound(char * src, int time)
{
	int i, j, tmp;
	int len = strlen(src);
	time %= len; //长度为5的情况下，旋转6、11、16...次相当于1次，7、12、17...次相当于2次，以此类推。
	for (i = 0; i < time; i++) //执行k次的单次平移
	{
		tmp = src[0];
		for (j = 0; j < len - 1; j++) //单次平移
		{
			src[j] = src[j + 1];
		}
		src[j] = tmp;
	}
}

int main()
{
	char a[] = "abcd";
	int time = 0;
	printf("请输入你要左旋转的个数\n");
	scanf("%d", &time);
	leftRound(a, time);
	printf("%s", a);
}

但是这种方法太繁杂，需要一个一个左旋，时间复杂度为O（n^n)。

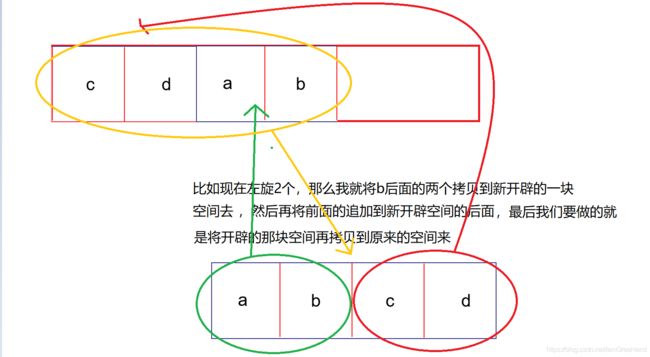
方法二：拼接法

方法二较之前方法一在时间复杂度上大大的提高了，方法二的时间复杂度为：O（n），下面来看具体实现过程，你就会明白为什么是O（n）了。

代码实现

void leftRound(char * src, int time)
{
	int len = strlen(src);
	int pos = time % len; //断开位置的下标
	char tmp[256] = { 0 }; //更准确的话可以选择malloc len + 1个字节的空间来做这个tmp

	strcpy(tmp, src + pos); //先将后面的全部拷过来
	strncat(tmp, src, pos); //然后将前面几个接上
	strcpy(src, tmp); //最后拷回去
}

int main()
{
	char a[] = "abcd";
	int time = 0;
	printf("请输入你要左旋转的个数\n");
	scanf("%d", &time);
	leftRound(a, time);
	printf("%s", a);
}

这个方法要用到一个数组形成的辅助空间，所以也不是很好

方法三：三次逆序法

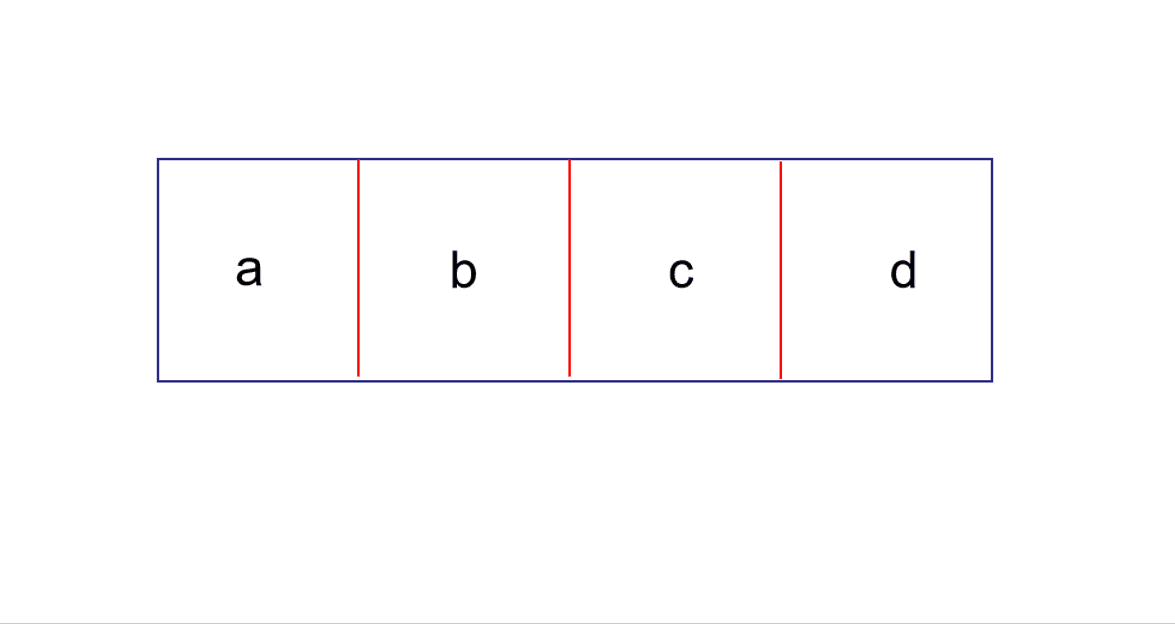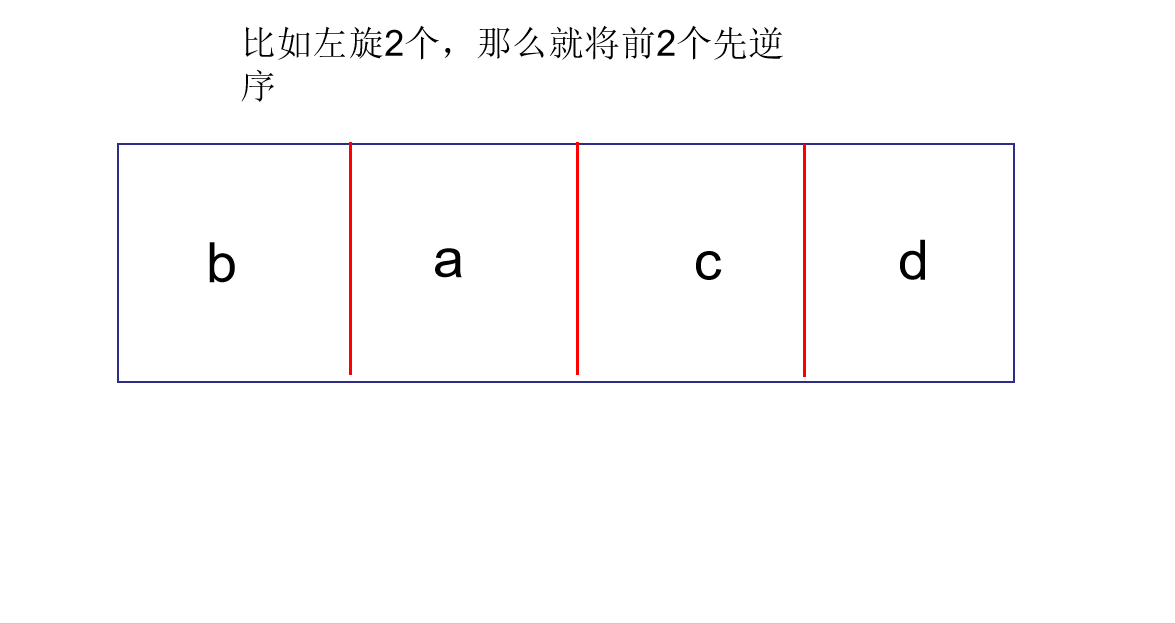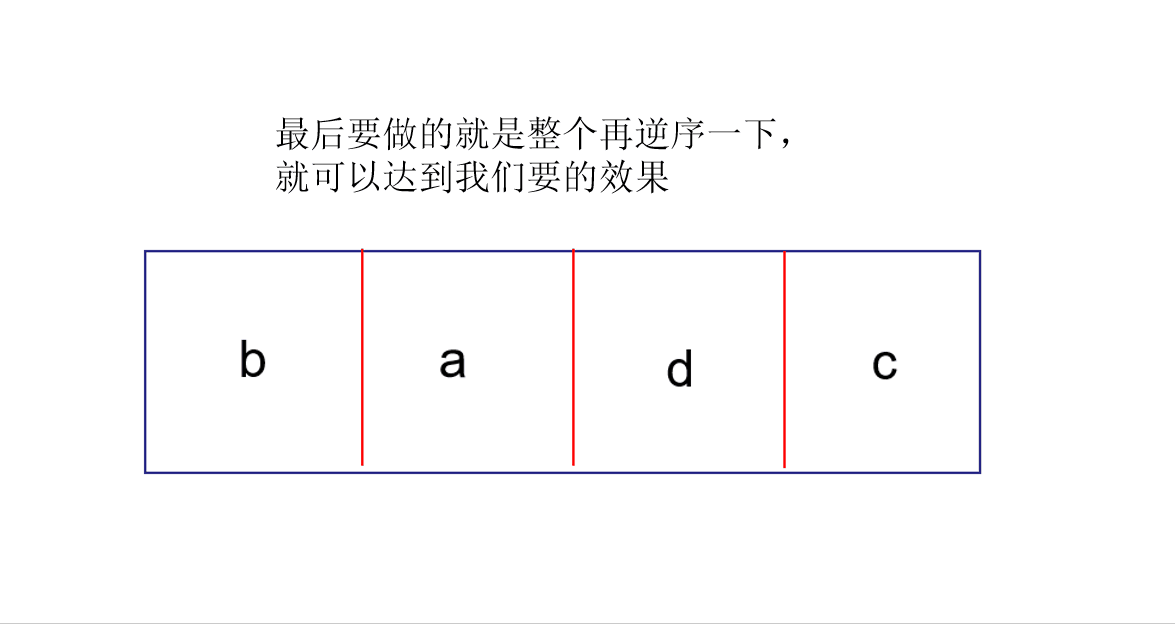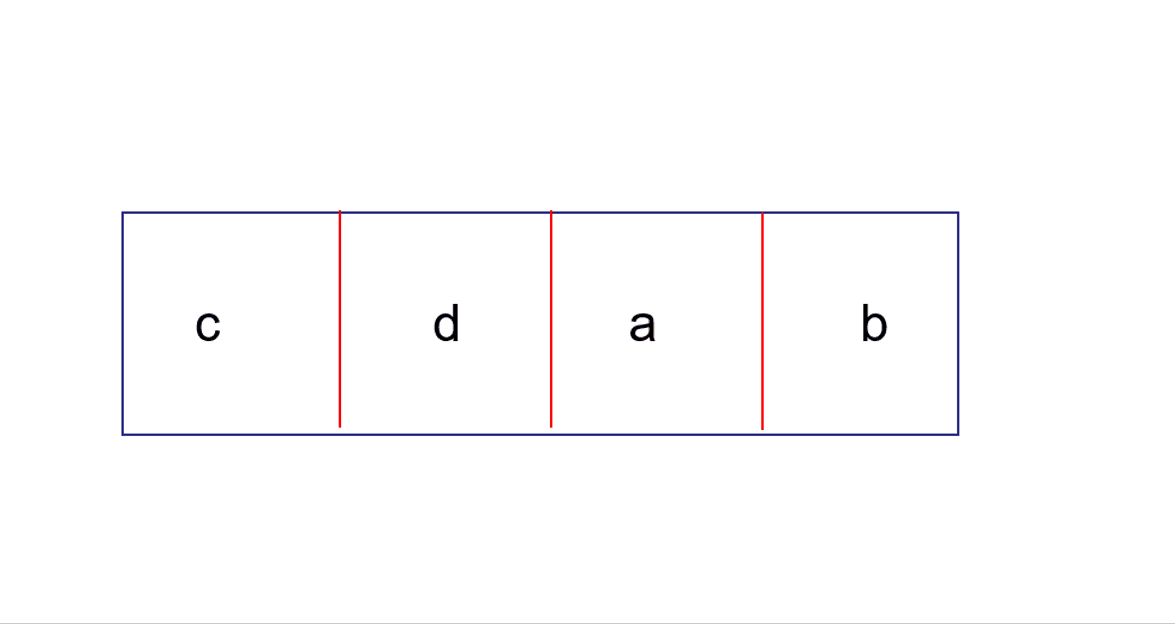
例如ABCDEFG，左旋3次后变成DEFGABC，有一个特殊的操作方式：
先将要左旋的前三个家伙逆序（CBADEFG），然后将后半段也逆序（CBAGFED），最后整体逆序（DEFGABC）即可。这样只需要做数值交换即可，可以写一个函数帮我们完成局部逆序

这种方法既不需要额外开辟空间，而且时间复杂度也为O（n）

代码实现

void reverse_part(char *str, int start, int end) //将字符串从start到end这一段逆序
{
	int i, j;
	char tmp;

	for (i = start, j = end; i < j; i++, j--)
	{
		tmp = str[i];
		str[i] = str[j];
		str[j] = tmp;
	}
}

void leftRound(char * src, int time)
{
	int len = strlen(src);
	int pos = time % len;
	reverse_part(src, 0, pos - 1); //逆序前段
	reverse_part(src, pos, len - 1); //逆序后段
	reverse_part(src, 0, len - 1); //整体逆序
}

int main()
{
	char a[] = "abcd";
	int time = 0;
	printf("请输入你要左旋转的个数\n");
	scanf("%d", &time);
	leftRound(a, time);
	printf("%s", a);
}

题目3.字符串旋转结果

写一个函数，判断一个字符串是否为另外一个字符串旋转之后的字符串。
例如：给定s1 =AABCD和s2 = BCDAA，返回1
给定s1=abcd和s2=ACBD，返回0.
AABCD左旋一个字符得到ABCDA
AABCD左旋两个字符得到BCDAA
AABCD右旋一个字符得到DAABC

解决思路

方法一：利用方法二来实现

如果你是旋转后的结果，那么我一定可以通过左旋来得到，如果得不到，那就不是选择后的结果。当做完题目二后，其实这种解法也就很容易写出来了。

代码实现

void reverse_part(char *str, int start, int end) 
{
	int i, j;
	char tmp;

	for (i = start, j = end; i < j; i++, j--)
	{
		tmp = str[i];
		str[i] = str[j];
		str[j] = tmp;
	}
}

int judge(char *s1, char *s2, int sz)
{
	int len = sz;
	while (sz--)
	{
			reverse_part(s1, 0, sz - 1); 
			reverse_part(s1, sz, len - 1); 
			reverse_part(s1, 0, len - 1); 
			if (strcmp(s1, s2) == 0)
			{
				return 1;
			}
	}
	return 0;
}

int main()
{
	char s1[] = "abcd";
	char s2[] = "cdab";
	int sz = strlen(s1);
	printf("%d",judge(s1, s2, sz));
	return 0;
}

方法二：重复法（题目二也可以利用此方法解决）

其实ABCDE无论怎么旋，旋转后的所有结果，都包含在了ABCDEABCD这个字符串里了。所以做法很简单，只需要将原字符串再来一遍接在后面，然后找一找待查找的字符串是不是两倍原字符串的子集即可。

代码实现

int findRound(const char * src, char * find)
{
	char tmp[256] = { 0 }; //用一个辅助空间将原字符串做成两倍原字符串
	strcpy(tmp, src); //先拷贝一遍
	strcat(tmp, src); //再连接一遍
	return strstr(tmp, find) != NULL; //看看找不找得到
}

int main()
{
	char s1[] = "abcd";
	char s2[] = "cdab";
	printf("%d", findRound(s1, s2));
	return 0;
}

相比之方法一，方法一的时间复杂度为O(n^n),因为它嵌套了两层循环；而方法二就大大提升了效率，时间复杂度只有O(n)，不过要浪费一些空间。