归并排序O(nlgn)

大家好，我是蓝胖子，我一直相信编程是一门实践性的技术，其中算法也不例外，初学者可能往往对它可望而不可及，觉得很难，学了又忘，忘其实是由于没有真正搞懂算法的应用场景，所以我准备出一个系列，囊括我们在日常开发中常用的算法，并结合实际的应用场景，真正的感受算法的魅力。

代码已经上传github

https://github.com/HobbyBear/codelearning/tree/master/mergesort

算法原理

每每实现算法的时候，我总是倾向于用文字将算法的逻辑描述出来，当你能清晰的描述算法逻辑的时候，实现起来就是水到渠成的事情。

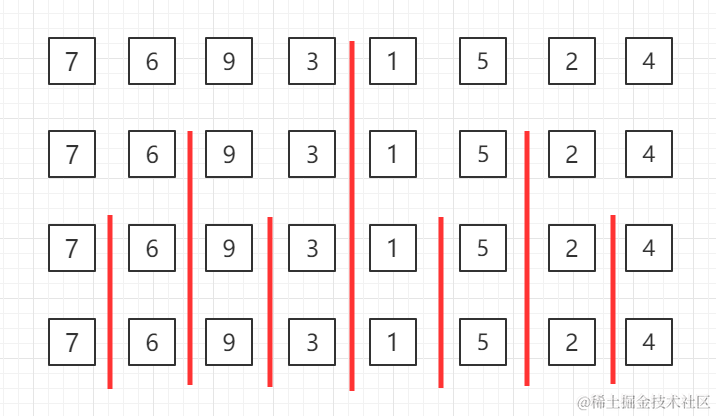
所以，我们接下来首先看下归并排序的算法逻辑。归并排序的时间复杂度是O(nlgn) ，它要求每次 将数组一分为二,被分割的数组又一分为二直至不能被分割，最后由底向上进行两两合并。你可以看到，假设数组长度是n，整个过程一共有lg n层，每一层需要对n个元素进行合并，所以时间复杂度是O(nlgn) 。如下图所示:

合并的过程是将合并的两个有序数组的元素变成一个有序数组的过程，我们把这个过程称为merge，于是我们将 归并排序的详细步骤总结为如下的步骤，

1，将数组一分为二,形成左右子数组。

2，对左子数组进行归并排序。

3，对右子数组进行归并排序。

4，对左右子数组进行merge。

详细的merge操作我们可以在O(n)时间复杂度内完成，详细步骤可以总结如下:

1，用i表示左子数组当前遍历的元素，j表示右边子数组当前遍历的元素。

2，创建一个新数组，用于保存排好序的元素，开始遍历左右子数组，如果左右子数组都没有遍历完，则比较各自当前遍历元素的大小，将小的元素复制到新数组，然后移动小元素所在数组当前遍历的指针指向下一个遍历元素。

3，如果其中一个数组遍历完成则只需要将，没有遍历完的那个数组剩下元素全部复制到新数组即可。

实现

了解了上述详细步骤后，我们可以很容易的用递归实现上述归并排序逻辑。

// 将数组[l...r]一分为二，分别对左右数组进行排序，然后对排序好的数组进行归并  
func mergesort(arr []int, l, r int) {  
   if l >= r {  
      return  
   }  
   mid := (l + r) / 2  
   mergesort(arr, l, mid)  
   mergesort(arr, mid+1, r)  
   merge(arr, l, mid, r)  
}

merge 部分代码如下，

写算法逻辑的时候一定要注意边界条件，比如我这里定义的是闭区间，那么下面的逻辑都是按闭区间去写的。

// [l...mid] [mid+1...r]  
func merge(arr []int, l, mid, r int) {  
   arr1 := arr[l : mid+1]  
   arr2 := arr[mid+1 : r+1]  
   newArr := make([]int, r-l+1)  
   i := 0 // 当前遍历元素  
   j := 0  
   k := 0  
   for i < len(arr1) && j < len(arr2) {  
      if arr1[i] > arr2[j] {  
         newArr[k] = arr2[j]  
         j++  
         k++  
         continue  
      }  
      newArr[k] = arr1[i]  
      k++  
      i++  
   }  
   if i == len(arr1) {  
      copy(newArr[k:], arr2[j:])  
   }  
   if j == len(arr2) {  
      copy(newArr[k:], arr1[i:])  
   }  
   copy(arr[l:], newArr)  
}

应用 求解逆序对的数量

关于归并排序的一个应用，我这里用leetcode一个题举例，这个题是leetcode 的剑指 Offer 51题，求解逆序对。

剑指 Offer 51. 数组中的逆序对  
困难  
1.1K  
相关企业  
在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组，求出这个数组中的逆序对的总数。  
  
示例 1:  
输入: [7,5,6,4]  
输出: 5  
  
限制：  
  
0 <= 数组长度 <= 50000

这道题可以采用归并排序的思想，在merge时，得到逆序对的数量，如下,

merge时的两个数组是有序的，且归并排序的左右数组的相对顺序是不变的，当右边数组合并到左边数组时，如果左边的数组元素大，则说左边数组当前遍历的元素和其以后的元素都可以和右边的数组构成一个逆序对。

所以我们可以在merge的代码逻辑中添加一段累计逆序对的逻辑，如下:

func mergeCopy(arr []int, l, mid, r int, cnt *int) {  
   arr1 := arr[l : mid+1]  
   arr2 := arr[mid+1 : r+1]  
   newArr := make([]int, r-l+1)  
   i := 0 // 当前遍历元素  
   j := 0  
   k := 0  
   for i < len(arr1) && j < len(arr2) {  
      if arr1[i] > arr2[j] {  
         newArr[k] = arr2[j]  
         //  新增cnt 变量用于保存逆序对的数量
         *cnt += len(arr1) - i  
         j++  
         k++  
         continue  
      }  
      newArr[k] = arr1[i]  
      k++  
      i++  
   }  
   if i == len(arr1) {  
      copy(newArr[k:], arr2[j:])  
   }  
   if j == len(arr2) {  
      copy(newArr[k:], arr1[i:])  
   }  
   copy(arr[l:], newArr)  
}