1.1线性模型

1.1线性模型

以下是一组用于回归的方法，其中目标值预计是特征的线性组合。

在数学符号中，如果是预测值。

在整个模块中，我们将向量指定为 coef_ 和intercept_。要使用广义线性模型执行分类，请参阅逻辑回归。

1.1.1.普通最小二乘

LinearRegression 使用系数拟合线性模型，以最小化数据集中观察到的目标与线性近似预测的目标之间的残差平方和。从数学上讲，它解决了以下形式的问题：

LinearRegression 将采用其拟合方法数组 X, y 并将线性模型的系数存储在其 coef_ 成员中：

>>> from sklearn import linear_model
>>> reg = linear_model.LinearRegression()
>>> reg.fit([[0, 0], [1, 1], [2, 2]], [0, 1, 2])

>>> reg.coef_

array([0.5, 0.5])

普通最小二乘法的系数估计依赖于特征的独立性。当特征相关且设计矩阵X的列具有近似线性相关性时，设计矩阵变得接近奇异（方阵的向量之间线性相关），结果，最小二乘估计对观察到的目标中的随机误差高度敏感，产生很大的方差。例如，在没有实验设计的情况下收集数据时，可能会出现这种多重共线性的情况。
例子：
线性回归示例

1.1.1.1.非负最小二乘法

可以将所有系数限制为非负，这在它们表示某些物理或自然非负量（例如，频率计数或商品价格）时可能很有用。 LinearRegression 接受一个布尔正参数：当设置为 True 非负最小二乘法时，然后应用。
例子：
非负最小二乘法

1.1.1.2.普通最小二乘复杂度

最小二乘解是使用 X 的奇异值分解计算的。如果 X 是形状为 (n_samples, n_features) 的矩阵，则此方法的成本为
，假设 。

1.1.2.岭回归和分类

1.1.2.1.回归

岭回归通过对系数的大小施加惩罚来解决普通最小二乘法的一些问题。岭系数最小化惩罚残差平方和：
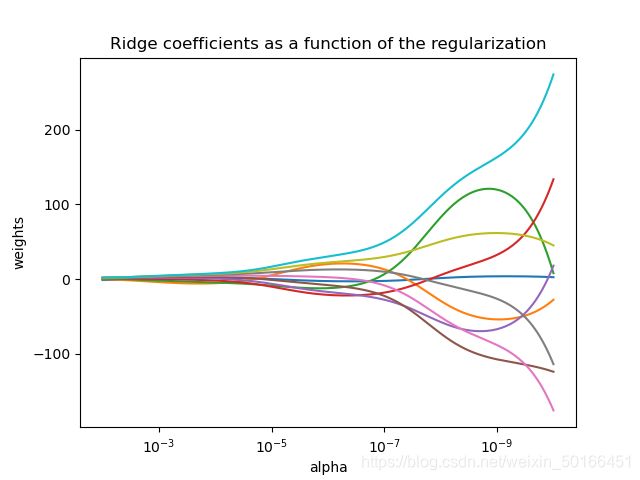
复杂度参数α≥0控制收缩量：α的值越大，收缩量越大，因此系数对共线性变得更加稳健。

与其他线性模型一样，Ridge 将采用其拟合方法数组 X, y 并将线性模型的系数存储在其 coef_ 成员中：

>>> from sklearn import linear_model
>>> reg = linear_model.Ridge(alpha=.5)
>>> reg.fit([[0, 0], [0, 0], [1, 1]], [0, .1, 1])

Ridge(alpha=0.5)

>>> reg.coef_

array([0.34545455, 0.34545455])

>>> reg.intercept_

0.13636363636363638

思考：X=[0, 0; 0, 0;1, 1],w=(w0,w1,w2),y=[0; 0.1; 1]。若不添加惩罚则需要最小化【(w0+0+0-0)² + (w0+0+0-0.1)²+(w0+w1+w2-1)²】分别对w0,w1,w2求导得到：
3w0-0.1+w1+w2-1=0与w0+w1+w2-1=0。求解得到w0=0.05,w1+w2=0.95。其中对w1和w2的具体取值并无限制，但从对属性的作用来看，两者似乎并无区别，各取0.95/2为较佳选择。
容易看出y中的0.1相为随机误差所导致，若为0时，得到3w0+w1+w2-1=0。。从对属性的作用来看，三者的比例应为1：3：3为较佳选择，即w0=1/7(0.142857),w1=w2=3/7（约0.42857）。****但w0因为随机误差而被确定了为0.005，这显然不是我们所希望看到的。****惩罚函数为α（w0²+w1²+w2²）,我们需要最小化【(w0)² + (w0-0.1)²+(w0+w1+w2-1)²+α（w0²+w1²+w2²）】得：

• (3+α)w0+w1+w2-1.1=0
• w0+(1+α)w1+w2-1=0
• w0+w+(1+α)w2-1=0
  由2，3知w1与w2数量相等，罚函数不改变正确的比例。对比1与3w0+w1+w2-1=0，罚函数相当于用αw0减弱了0.1的随机误差带来的影响。
  从数学上来看，若有随机误差产生，相互于产生一种波动，拟合超直线会迎合这种波动从而产生偏离（调整截距与斜率）以降低最小二乘法判据下的误差，这必然导致截距与斜率的波动，罚函数将这种波动的最小化任务也算在优化之中，从而抑制随机误差的影响。

1.1.2.2. 分类

岭回归者有一个分类变种：岭分类器RidgeClassifier。此分类器首先将二进制目标转换为 {-1，1}，然后将问题视为回归任务，优化与上述相同的目标。预测类对应于回归器预测的标志（+/-）。对于多类分类，该问题被视为多产出回归，预测类对应于具有最高值的输出。
使用（惩罚性）最小正方形损失来适应分类模型而不是更传统的logistic 或 hinge losses.似乎值得怀疑。然而，在实践中，所有这些模型都可能导致在准确性或精度/召回方面出现类似的交叉验证分数，而RidgeClassififer 使用的受罚最小二乘损失允许对具有不同计算性能配置文件的数字解算器进行截然不同的选择。
RidgeClassifer 的速度可以明显快于具有大量类的 LogisticRegression，因为它只需要计算一次投影矩阵。
此分类器有时称为具有线性内核的最小二乘支持向量机。
例子：

• 绘图岭系数作为规范化的函数
• 使用稀疏功能对文本文档进行分类
• 线性模型系数解释中的常见陷阱
  （未完待续…）