算法基础之数组双指针(Leetcode题型归纳)
数组双指针(Leetcode题型归纳)
- 1.前言
- 2.双指针基础
- 3.相向双指针
-
- 3.1定义
- 3.2真题分析
-
- 3.2.1两数之和(1)
- 3.2.2两数之和-输入有序数组(167)
- 3.2.3三数之和(15)
- 3.2.4最接近的三数之和(16)
- 3.2.5四数之和(18)
- 3.2.6盛最多水的容器(11)
- 3.2.7有效三角形的个数(611)
- 4.同向双指针-快慢指针
-
- 4.1定义
- 4.2真题分析
-
- 4.1.1删除排序数组中的重复项(26)
- 4.1.2移除元素(27)
- 4.1.3删除排序数组中的重复项(80)
- 4.1.4移动零(283)
- 4.1.5数组中的最长山脉(845)
- 4.1.6水果成篮(904)
- 5.同向双指针-滑动窗口
-
- 5.1定义
- 5.2真题分析
-
- 5.2.1滑动窗口最大值(239)
- 5.2.2长度最小的子数组(209)
- 5.2.3乘积小于K的子数组(713)
- 6.分离双指针
-
- 6.1定义
- 6.2真题分析
-
- 6.2.1两个数组的交集(350)
- 6.2.1两个数组的交集(349)
1.前言
在系统复习一遍数组的理论基础后,我们开始归纳Leetcode中的一种题型:数组双指针。归纳是很痛苦的过程,也是最有成就感的事情,希望大家也能多指出我的不足。
2.双指针基础
所谓双指针算法,就是指的是在遍历的过程中,不是普通的使用单个指针进行循环访问,而是使用两个相同方向或者相反方向的指针进行扫描,从而达到相应的目的。双指针法充分使用了数组有序这一特征,从而在某些情况下能够简化一些运算,降低时间复杂度。

一般来说,双指针算法分成下面四类:
- 相向双指针
- 同向双指针 - 快慢指针
- 同向双指针 - 滑动窗口
- 分离双指针
3.相向双指针
3.1定义
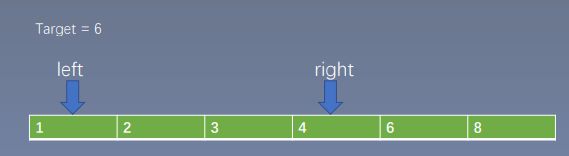
指在有序数组中,将指向最左侧的索引定义为左指针 (left),最右侧的定义为右指针 (right),然后从两头向中间进行数组遍历。
相关题目如下:

3.2真题分析
3.2.1两数之和(1)
Given an array of integers nums and an integer target, return indices of the two numbers such that they add up to target.
You may assume that each input would have exactly one solution, and you may not use the same element twice.
You can return the answer in any order.
Example 1:
Input: nums = [2,7,11,15], target = 9
Output: [0,1]
Output: Because nums[0] + nums[1] == 9, we return [0, 1].
Example 2:
Input: nums = [3,2,4], target = 6
Output: [1,2]
Example 3:
Input: nums = [3,3], target = 6
Output: [0,1]
Constraints:
2 <= nums.length <= 104-109 <= nums[i] <= 109-109 <= target <= 109- Only one valid answer exists.
Follow-up: Can you come up with an algorithm that is less than O(n2) time complexity?
后面也会尽量附上中文版本题目方便大家读题:

一开始,我会想到去用暴力解法吧:枚举数组中的每一个数 x,寻找数组中是否存在 target - x。当我们使用遍历整个数组的方式寻找 target - x 时,需要注意到每一个位于 x 之前的元素都已经和 x 匹配过,因此不需要再进行匹配。而每一个元素不能被使用两次,所以我们只需要在 x 后面的元素中寻找 target - x。
#两数之和-暴力解法
class Solution:
def twoSum(self, nums, target):
"""
:type nums: List[int]
:type target: int
:rtype: List[int]
"""
l = len(nums)
for i in range(l-1):
for j in range(i+1,l):
if nums[i] + nums[j] == target:
return [i,j]
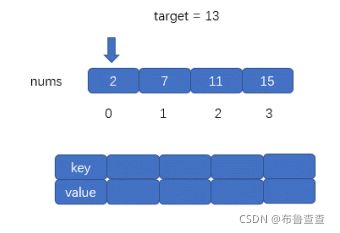
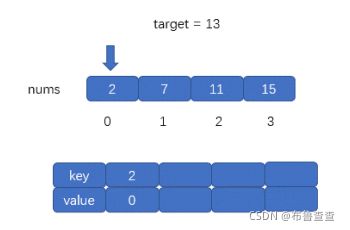
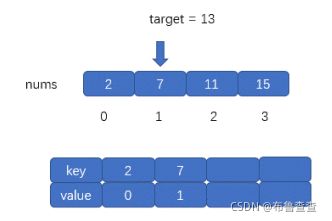
然而,暴力解法时间复杂度是O(n*2),不太理想,原因是寻找target - x这部分时间复杂度比较高。所以,我又探索了用哈希表去解决这个问题。简单来说,我们可以把哈希表看作一个字典,这样我们创建一个哈希表,对于每一个 x,我们首先查询哈希表中是否存在 target - x,然后将 x 插入到哈希表中,即可保证不会让 x 和自己匹配。



#两数之和-哈希解法
class Solution:
def twoSum(self, nums, target):
map = {} #创建一个哈希表
for i in range(len(nums)):
if target - nums[i] not in map:
map[nums[i]] = i
else:
return map[target - nums[i]], i
这时时间复杂度是O(n)了。But,这好像跟双指针没什么关系欸,我们现在来讲双指针的思路:L指针用来指向第一个值,R指针用来从第L指针的后面查找数组中是否含有和L指针指向值和为目标值的数。两个指针分别从左从右开始扫描,每次判断这两个数相加是不是target,如果小了,那就把左边的指针向右移,同理右指针。


#两数之和-双指针解法
class Solution:
def twoSum(self, nums, target):
array = nums.copy() #浅拷贝,保留原来数组
nums.sort() #排序
i, j = 0, len(nums)-1 #两指针一头一尾
while i<j:
s = nums[i] + nums[j]
if s<target:
i += 1
elif s>target:
j -= 1
else:
break
res = []
for k in range(len(nums)):
if array[k] == nums[i] or array[k] == nums[j]:
res.append(k)
return res
这时候时间复杂度也是O(n)的。然而,如果我们把题目改一下:

此时我们不再需要返回index,而是返回值了。那么有个好处是,我不用再copy数组了,因为之前是为了防止index改变了。
#两数之和-魔改
class Solution:
def twoSum(self, nums, target):
nums.sort() #先对数组排序
lo, hi = 0, len(nums)-1 #左右指针
while lo<hi:
s = nums[lo] + nums[hi]
if s<target:
lo += 1
elif s>target:
hi -= 1
elif s == target:
return [nums[lo],nums[hi]]
emmm我再改一下题目:

这个时候要返回所有和为target的元素对了,而且不能重复哦,那我就把这些元素对存到一个数组res里咯。另外如果有下图这样的情况,可能就会出现重复元素对的情况,就要去跳过了。
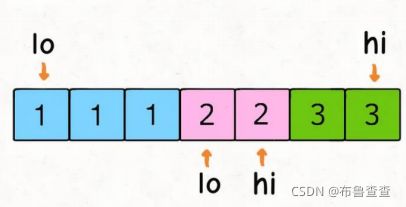
#两数之和-再魔改
class Solution:
def twoSumTarget(self, nums, target):
nums.sort()#先对数组排序,这个内置的算法是O(nlogn)
res = []
lo, hi = 0, len(nums)-1 #左右指针
left = nums[lo]
right = nums[hi]
while lo<hi:
s = nums[lo] + nums[hi]
if s<target:
lo += 1
elif s>target:
hi -= 1
elif s == target:
res.append([nums[lo],nums[hi]])
while lo < hi and nums[lo] == left:
lo += 1
while lo < hi and nums[hi] == right:
hi -= 1
return res
这个例子的时间复杂度是O(nlogn)的(因为sort方法是这样),是比O(n)大的。
3.2.2两数之和-输入有序数组(167)
Given an array of integers numbers that is already sorted in non-decreasing order, find two numbers such that they add up to a specific target number.
Return the indices of the two numbers (1-indexed) as an integer array answer of size 2, where 1 <= answer[0] < answer[1] <= numbers.length.
The tests are generated such that there is exactly one solution. You may not use the same element twice.
Example 1:
Input: numbers = [2,7,11,15], target = 9
Output: [1,2]
Explanation: The sum of 2 and 7 is 9. Therefore index1 = 1, index2 = 2.
Example 2:
Input: numbers = [2,3,4], target = 6
Output: [1,3]
Example 3:
Input: numbers = [-1,0], target = -1
Output: [1,2]
1. 使用双指针,一个指针指向值较小的元素,一个指针指向值较大的元素。指向较小元素的指针从头向尾遍历,指向较大元素的指针从尾向头遍历。
2. 如果两个指针指向元素的和 sum == target,那么得到要求的结果;
3. 如果 sum > target,移动较大的元素,使 sum 变小一些;如果 sum < target,移动较小的元素,使 sum变大一些。
#167两数之和
class Solution:
def twoSum(self, numbers: List[int], target: int) -> List[int]:
low, high = 0, len(numbers) - 1
while low < high:
total = numbers[low] + numbers[high]
if total == target:
return [low + 1, high + 1]
elif total < target:
low += 1
else:
high -= 1
return [-1, -1]
3.2.3三数之和(15)
Given an integer array nums, return all the triplets [nums[i], nums[j], nums[k]] such that i != j, i != k, and j != k, and nums[i] + nums[j] + nums[k] == 0.
Notice that the solution set must not contain duplicate triplets.
Example 1:
Input: nums = [-1,0,1,2,-1,-4]
Output: [[-1,-1,2],[-1,0,1]]
Example 2:
Input: nums = []
Output: []
Example 3:
Input: nums = [0]
Output: []

此题是medium难度的,如果暴力求解是O(n*3)的,绝对不行滴。但基于前面两数之和,我们想到可以采取固定一个数,同时用双指针来查找另外两个数的方式。

具体思路如下:
1. 我们可以先对数组进行排序,然后我们选择一个数字做 C 位,然后我们在这个 C 位数字的右边进行双指针搜索。
2. 从最左边 i+1(最小值)和最右边 len(nums)-1(最大值)两个数字开始,加上 C 位,计算总和是否等于 0。 如果大于0,说明实力太强了,就把右侧的数字左移一位。 如果小于 0,说明实力太弱了,就把左边的数字右移一位。
3. 当双指针碰到的时候,这轮循环结束,以该数字为 C 位的所有可能都已经尝 试完毕了。

#三数之和
class Solution:
def threeSum(self,nums):
# 排序
nums.sort()
# 单循环+双指针
res = []
for i in range(len(nums)):
# 去重(如果当前C位数和相邻的数相等,直接移动指针)
if i > 0 and nums[i] == nums[i-1]:
continue
left = i + 1
right = len(nums) - 1
while left < right:
if nums[i] + nums[left] + nums[right] > 0:
right -= 1
elif nums[i] + nums[left] + nums[right] < 0:
left += 1
elif nums[i] + nums[left] + nums[right] == 0:
res.append([nums[i],nums[left],nums[right]])
# 去重(如果当前数和相邻的数相等,直接移动指针)
while left < right and nums[left] == nums[left+1]:
left += 1
while left < right and nums[right] == nums[right-1]:
right -= 1
left += 1
right -= 1
return res
3.2.4最接近的三数之和(16)
Given an integer array nums of length n and an integer target, find three integers in nums such that the sum is closest to target.
Return the sum of the three integers.
You may assume that each input would have exactly one solution.
Example 1:
Input: nums = [-1,2,1,-4], target = 1
Output: 2
Explanation: The sum that is closest to the target is 2. (-1 + 2 + 1 = 2).
Example 2:
Input: nums = [0,0,0], target = 1
Output: 0

具体思路如下:
1、在数组 nums 中,进行遍历,每遍历一个值利用其下标 i,形成一个固定值nums[i]。
2、使用前指针指向 left = i + 1 处,后指针指向 right = len(nums) - 1 处,也就是结尾处,根据 sums = nums[i] + nums[left] + nums[right] 的结果,判断 sums 与目标 target 的距离,如果更近则更新结果 a。
3、因为数组有序,如果 sums > target 则 right -= 1,如果 sums < target 则 left += 1,如果 sums == target 则说明距离为 0,直接返回结果。
#最接近的三数之和
class Solution:
def threeSumClosest(self, nums: List[int], target: int) -> int:
# 排序
nums.sort()
# 初始化
a = abs(nums[0] + nums[1] + nums[2] - target)
res = nums[0] + nums[1] + nums[2]
for i in range(len(nums)):
left = i + 1
right = len(nums) - 1
# 当前nums[i]情况下,搜索最接近的组合
while left < right:
sums = nums[i] + nums[left] + nums[right]
# 比较sums与目标target的距离与之前最近的距离,如果更近则更新
if abs(sums-target) < a:
a = abs(sums-target)
res = sums
if sums > target:
right -= 1
elif sums < target:
left += 1
# 如果sums == target,则说明距离为0,这就是最接近的数
elif sums == target:
return sums
return res
3.2.5四数之和(18)
Given an array nums of n integers, return an array of all the unique quadruplets [nums[a], nums[b], nums[c], nums[d]] such that:
0 <= a, b, c, d < na,b,c, anddare distinct.nums[a] + nums[b] + nums[c] + nums[d] == target
You may return the answer in any order.
Example 1:
Input: nums = [1,0,-1,0,-2,2], target = 0
Output: [[-2,-1,1,2],[-2,0,0,2],[-1,0,0,1]]
Example 2:
Input: nums = [2,2,2,2,2], target = 8
Output: [[2,2,2,2]]

哎呀就知道还要搞四数之和,但思路还是跟三数之和差不多,只不过三数是要单重循环第一个数,四数要两重循环前两个数。具体思路如下:
1、使用两重循环分别枚举前两个数,然后在两重循环枚举到的数之后使用双指针枚举剩下的两个数。假设两重循环枚举到的前两个数分别位于下标 i 和 j,其中 i
3、每次计算四个数的和,并进行如下操作:
如果和等于 target,则将枚举到的四个数加到答案中,然后将左指针右移直到遇到不同的数,将右指针左移直到遇到不同的数;
如果和小于target,则将左指针右移一位;
如果和大于 target,则将右指针左移一位。
当然,我们还要考虑去重,即剪枝操作:
1、在确定第一个数之后,如果nums[i]+nums[i+1]+nums[i+2]+nums[i+3]>target,说明此时剩下的三个数无论取什么值,四数之和一定大于 target,因此退出第一重
循环;
2、在确定第一个数之后,如果nums[i]+nums[n−3]+nums[n−2]+nums[n−1]
3、在确定前两个数之后,如果 nums[i]+nums[j]+nums[j+1]+nums[j+2]>target,说明此时剩下的两个数无论取什么值,四数之和一定大于 target,因此退出第二重循
环;
4、在确定前两个数之后,如果nums[i]+nums[j]+nums[n−2]+nums[n−1]
#四数之和
class Solution:
def fourSum(self, nums: List[int], target: int) -> List[List[int]]:
res = list()
if not nums or len(nums) < 4:
return res
nums.sort()
length = len(nums)
for i in range(length - 3):
if i > 0 and nums[i] == nums[i - 1]:
continue
if nums[i] + nums[i + 1] + nums[i + 2] + nums[i + 3] > target:
break
if nums[i] + nums[length - 3] + nums[length - 2] + nums[length - 1] < target:
continue
for j in range(i + 1, length - 2):
if j > i + 1 and nums[j] == nums[j - 1]:
continue
if nums[i] + nums[j] + nums[j + 1] + nums[j + 2] > target:
break
if nums[i] + nums[j] + nums[length - 2] + nums[length - 1] < target:
continue
left, right = j + 1, length - 1
while left < right:
total = nums[i] + nums[j] + nums[left] + nums[right]
if total == target:
res.append([nums[i], nums[j], nums[left], nums[right]])
while left < right and nums[left] == nums[left + 1]:
left += 1
left += 1
while left < right and nums[right] == nums[right - 1]:
right -= 1
right -= 1
elif total < target:
left += 1
else:
right -= 1
return res
如果出题人闲着没事继续出这种几数之和的题目呢?我们想想看,三数之和固定一个数,四数之和固定两个数…一百数之和固定九十八个数,那么n数之和就固定n-98个数咯,然后再用双指针一一解决就ok啦。
3.2.6盛最多水的容器(11)
Given n non-negative integers a1, a2, ..., an , where each represents a point at coordinate (i, ai). n vertical lines are drawn such that the two endpoints of the line i is at (i, ai) and (i, 0). Find two lines, which, together with the x-axis forms a container, such that the container contains the most water.
Notice that you may not slant the container.
Example 1:
Input: height = [1,8,6,2,5,4,8,3,7]
Output: 49
Explanation: The above vertical lines are represented by array [1,8,6,2,5,4,8,3,7].
In this case, the max area of water (blue section) the container can contain is 49.
Example 2:
Input: height = [1,1]
Output: 1
Example 3:
Input: height = [4,3,2,1,4]
Output: 16
Example 4:
Input: height = [1,2,1]
Output: 2
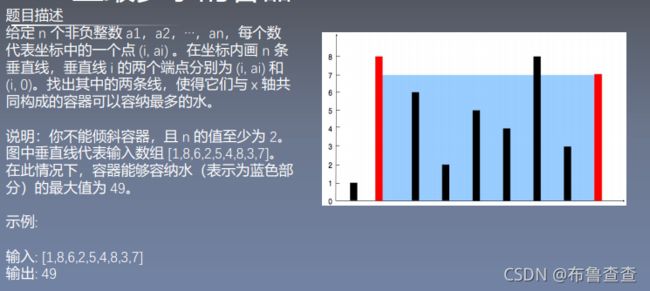
看到这题一下子思路不是很明确,先试试移动两边有什么效果吧。一开始如下图所示:

如果用双指针的思想,我们就放在最左和最右两边。
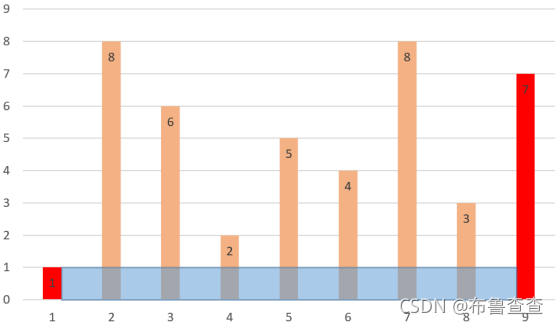
试着把右边的长板往左移动,发现面积变小了。

但是如果是把左边现在的短板往左边移动,发现面积是增大了。

如果再接着是按‘短板向内移动,长板不动’的思想操作,我们能做到所有的消去状态都不会导致丢失面积最大值。根据木桶原理,短板会决定桶里水最多能装多少,跟这里的情况差不多。
如果还是有点迷迷糊糊,我们用反证法来证明一下,即如果按‘短板不动,长板向内移动’的话,初始状态如下图:
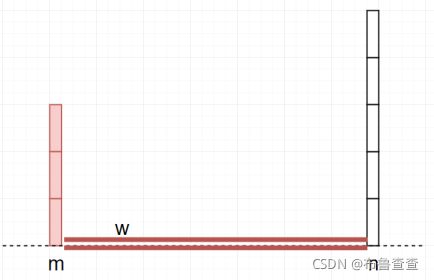
一种情况是长板向内移动后变得比短板更短,此时面积变小了。
另一种情况是长板向内移动后比短板长(甚至比原来的自己还长),但面积还是变小了,类似于木桶原理。
因此,可以根据这个思想来写我们代码啦。
#盛最多水
class Solution:
def maxArea(self, height: List[int]) -> int:
i, j, res = 0, len(height) - 1, 0
while i < j:
if height[i] < height[j]:
#记住是短板向长板移动,长板不动
res = max(res, height[i] * (j - i))
i += 1
else:
res = max(res, height[j] * (j - i))
j -= 1
return res
3.2.7有效三角形的个数(611)
Given an integer array nums, return the number of triplets chosen from the array that can make triangles if we take them as side lengths of a triangle.
Example 1:
Input: nums = [2,2,3,4]
Output: 3
Explanation: Valid combinations are:
2,3,4 (using the first 2)
2,3,4 (using the second 2)
2,2,3
Example 2:
Input: nums = [4,2,3,4]
Output: 4
第一反应应该思考怎么才能实现一个三角形呢,首先我们知道三角形的性质:任意两边之和大于第三边。那么我们确保最小的两边之和大于最长那条边,就能确保任意两边之和大于最长边了。然后我们需要先找到最长那条边,那么就需要排序咯。紧接着,就在剩下的边里找两条边(跟前面三数之和是不是有点类似)。具体思路如下:
数组排序,便于后序的处理
1、固定最长的边 c,然后采用双指针在其左侧寻找合适的 a、b:a 从最左侧开始(nums[0])、b 从最右侧开始(nums[i-1])
2、如果 nums[left] + nums[right] > nums[i],说明 [left,right]、[left+1,right]…[right-1,right] 均满足条件,以 nums[right] 为中间边的情况已全部考虑过,然后 right -= 1
3、如果 nums[left] + nums[right] <= nums[i],两边之和太小,需要增大,left += 1
#有效三角形个数
class Solution:
def triangleNumber(self, nums: List[int]) -> int:
# 排序
nums.sort()
count = 0
for i in range(2,len(nums)):
left = 0
right = i - 1
while left < right:
if nums[left] + nums[right] > nums[i]:
# 这些都可以:[left,right]、[left+1,right]...[right-1,right]
count += right - left
right -= 1
else:
left += 1
return count
4.同向双指针-快慢指针
4.1定义
快慢指针也是双指针,但是两个指针从同一侧开始遍历数组,将这两个指针分别定义为快指针(fast)和慢指针(slow),两个指针以不同的策略移动,直到两个指针的值相等(或其他特殊条件)为止,如 fast 每次增长两个,slow 每次增长一个。
相关真题如下:

4.2真题分析
4.1.1删除排序数组中的重复项(26)
Given an integer array nums sorted in non-decreasing order, remove the duplicates in-place such that each unique element appears only once. The relative order of the elements should be kept the same.
Since it is impossible to change the length of the array in some languages, you must instead have the result be placed in the first part of the array nums. More formally, if there are k elements after removing the duplicates, then the first k elements of nums should hold the final result. It does not matter what you leave beyond the first k elements.
Return k after placing the final result in the first k slots of nums.
Do not allocate extra space for another array. You must do this by modifying the input array in-place with O(1) extra memory.

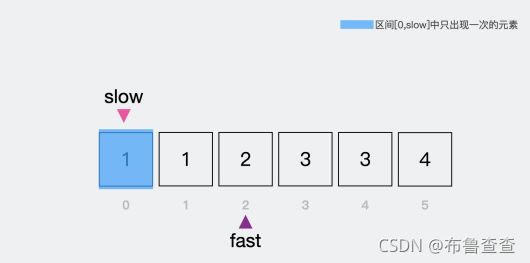
首先我们定义慢指针为索引0的位置,使得之后0到慢指针的位置之间(左闭右闭区间)只含有出现一次的元素;然后定义快指针为我们考察的元素,所以初始就定在了索引为1的位置。
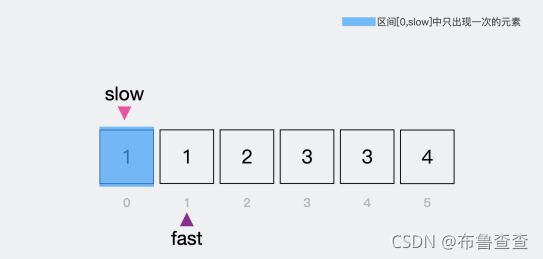
接下来快指针走到索引为2的位置,此时快慢指针的元素不一样,所以慢指针往右移动。
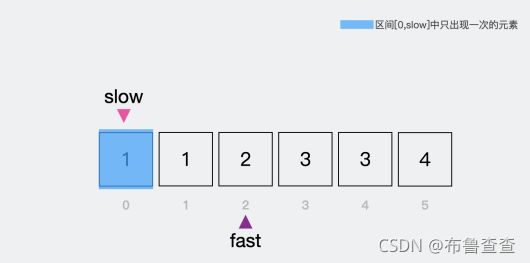
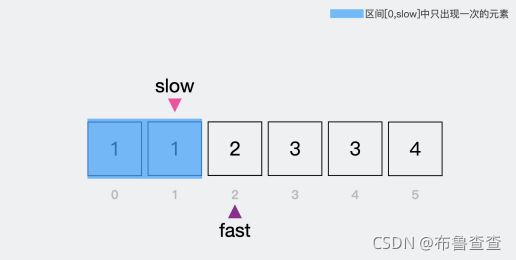
然后把快指针所指向的元素,赋给慢指针现在所指向的位置,这样【0,slow】里面才能只包含只出现一次的元素。
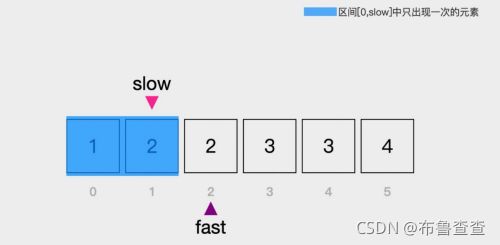
然后重复下去即可。
#leetcode26
class Solution:
def removeDuplicates(self, nums: List[int]) -> int:
i = 0
j = 1
while j < len(nums):
if nums[j] == nums[i]:
#两个元素相等,快指针移动
j += 1
else:
#两个元素不相等,慢指针扩大区间
i += 1
#快指针现在的值赋给慢指针的位置
nums[i] = nums[j]
#快指针继续往前挪
j += 1
return i+1
4.1.2移除元素(27)
Given an integer array nums and an integer val, remove all occurrences of val in nums in-place. The relative order of the elements may be changed.
Since it is impossible to change the length of the array in some languages, you must instead have the result be placed in the first part of the array nums. More formally, if there are k elements after removing the duplicates, then the first k elements of nums should hold the final result. It does not matter what you leave beyond the first k elements.
Return k after placing the final result in the first k slots of nums.
Do not allocate extra space for another array. You must do this by modifying the input array in-place with O(1) extra memory.
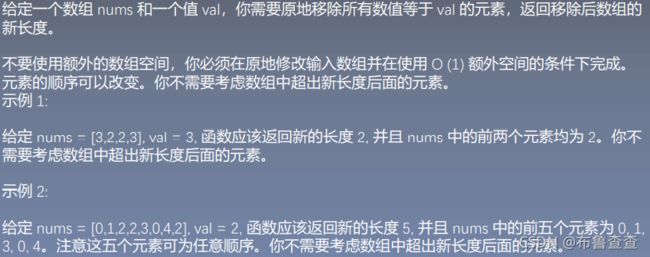
我们可以保留两个指针 i 和 j,其中 i 是慢指针,j 是快指针。当nums[j] 与给定的值相等时,递增 j 以跳过该元素。只要 nums[j] != val,我们就复制 nums[j] 到 nums[i] 并同时递增两个索引。重复这一过程,直到 j 到达数组的末尾,该数组的新长度为 i。
#leetcode 27
class Solution:
def removeElement(self, nums: List[int], val: int) -> int:
j = 0
last = len(nums)-1
while j <= last:
if nums[j] == val:
nums[j] = nums[last]
last -= 1
else:
j += 1
return last+1
4.1.3删除排序数组中的重复项(80)
Given an integer array nums sorted in non-decreasing order, remove some duplicates in-place such that each unique element appears at most twice. The relative order of the elements should be kept the same.
Since it is impossible to change the length of the array in some languages, you must instead have the result be placed in the first part of the array nums. More formally, if there are k elements after removing the duplicates, then the first k elements of nums should hold the final result. It does not matter what you leave beyond the first k elements.
Return k after placing the final result in the first k slots of nums.
Do not allocate extra space for another array. You must do this by modifying the input array in-place with O(1) extra memory.

遍历整个表:
把当前的元素与它前面的对比,如果二者元素相同(为重复元素):此时统计重复的计数器 count+=1。题目要求只保留 2 个重复的元素,这里需要加入重复元素个数的判断:
这个元素正好重复了 2 次 => 则进行保留。列表长度 i+=1,然后 nums[i]=nums[j];这个元素重复多于 2 次 => 不进行任何操作。体现在程序上不做处理把当前的元素与它前面的对比,如果二者元素不同(为新元素):此时把当前这个结点 (nums[j]) 添加到新表里面去,nums[i] = nums[j], 表长 i+1。
再重申慢指针的作用,就是划出一片区域,里面就是我们想要的东西。
#leetcode80
class Solution:
def removeDuplicates(self, nums: List[int]) -> int:
count = 1 #用来记录重复的次数
i = 0
j = 1
while j < len(nums):
# 二者元素相同(重复元素)
if nums[i] == nums[j]:
count += 1
# 这个元素正好重复了2次
if count == 2:
i += 1
nums[i] = nums[j]
# 这个元素重复多于2次
else:
pass
j += 1
# 二者元素不同(新元素)
else:
i += 1
nums[i] = nums[j]
count = 1
j += 1
return i+1
4.1.4移动零(283)
Given an integer array nums, move all 0's to the end of it while maintaining the relative order of the non-zero elements.
Note that you must do this in-place without making a copy of the array.

贯彻我们的理念(慢指针负责存放我们想要的东西,快指针负责完成一些筛选条件),慢指针的范围里存放非0的元素,快指针去遍历寻找非0的元素。因此思路是:
nums 中,i 指针用于存放非零元素
j 指针用于遍历寻找非零元素(注:j 指针找到一个非零元素后,方法nums[i] 的位置 i++,用于下一个 j 指针找到的非零元素)j 指针遍历完后,最后 nums 数组还有空位置,存放 0 即可。
#leetcode283
class Solution:
def moveZeroes(self, nums: List[int]) -> None:
i = 0
j = 0
# 双指针遍历寻找非零元素
while j < len(nums):
if nums[j] == 0:
j += 1
else:
nums[i] = nums[j]
i += 1
j += 1
# 空位置赋0
for k in range(i,len(nums)):
nums[k] = 0
4.1.5数组中的最长山脉(845)
You may recall that an array arr is a mountain array if and only if:
arr.length >= 3- There exists some index i (0-indexed) with
0 < i < arr.length - 1such that:
arr[0] < arr[1] < … < arr[i - 1] < arr[i]
arr[i] > arr[i + 1] > … > arr[arr.length - 1]
Given an integer array arr, return the length of the longest subarray, which is a mountain. Return 0 if there is no mountain subarray.

首先固定山峰值,然后分别寻找左、右半边山脉的长度。
A[left] < A[left+1],继续向左寻找
A[right] < A[right-1],继续向右寻找
如果以当前山峰的山脉长度比最长山脉长,更新最长山脉。
注意:我们可以在只有当前点为山峰的情况(即 A[i-1] < A[i] and A[i+1] < A[i]),才在左右寻找最长山峰,这样可以大大降低搜索的次数。
#leetcode845
class Solution:
def longestMountain(self, A: List[int]) -> int:
if len(A) < 3:
return 0
res = 0
# 固定山峰
for i in range(1,len(A)-1):
# 只有当前点为山峰的情况,才在左右寻找最长山峰
if A[i-1] < A[i] and A[i+1] < A[i]:
left = i - 1
right = i + 1
# 左半边山脉的长度
while left >= 0 and A[left] < A[left+1]:
left -= 1
# 右半边山脉的长度
while right <= len(A)-1 and A[right] < A[right-1]:
right += 1
# 如果这个山脉比最长的山脉长,更新res
if right - left - 1 > res:
res = right - left - 1
return res
4.1.6水果成篮(904)
总结的滑动窗口模板:
// 模板
for () {
// 将新进来的右边的数据,计算进来
// 更新数据
// 判断窗口数据是否不满足要求了
while (窗口数据不满要求 && left < arrSize) {
// 移除left数据,更新窗口数据
left++;
}
right++;
}
首先,这题的题意要理解一下,它其实就是要求一个最长的连续子序列,同时这个子序列的元素种类不能超过2种。
其次,我们可以用双指针的方法来求解这个题,为什么要用双指针呢?例如[1,2,3,3,3],从前往后遍历的话,可以获得[1,2],[2,3,3,3]两个子序列,最长的是后者,答案是4。重点是要发现,除了第一个子序列,后面的每一个子序列都要从前面的子序列里的某种元素开始,如[2,3,3,3]要从[2]开始,而[2]是前一个子序列的元素之一。再比如[1,2,1,3,3,3],可以获得[1,2,1],[1,3,3,3]两个符合条件的子序列,这时[1,3,3,3]要从[1]开始。
因此可以想到,用一个右指针j和左指针i。右指针用于往右探,左指针用于指示每一个新的子序列要重前面那个序列里继承哪一位。
那么是继承哪一位呢?其实这是有规律的,从前面两个例子可以看到,继承的既不一定是第一个类别,也不一定是第二个类别,实际上规律是,继承翻转的那一个种类,例如[1,2,1,3,3,3],j往右遍历的时候,如果当前的种类与i的种类不同,那么就令i=j,其中i就指示了下一个子序列的起点。本篇解法的关键就在这个翻转的规律上。
这样可以写出如下代码,核心是:j往前遍历的时候,如果超过2种水果了,那么j就回退到i的位置重新开始遍历。
class Solution:
def totalFruit(self, fruits: List[int]) -> int:
ans, n = 0, len(fruits)
i, j = 0, 0
types = {}
while j < n:
if len(types) == 2 and types.get(fruits[j]) is None: # 当前水果不可加入
types = {}
j = i # j回退到最后一次翻转的位置
else: # 当前水果可加入
types[fruits[j]] = types.get(fruits[j], 0) + 1
if fruits[j] != fruits[i]: # 水果有翻转 用i记录下翻转的位置
i = j
j += 1
ans = max(ans, sum(types.values()))
return ans
5.同向双指针-滑动窗口
5.1定义
有些时候,我们需要获得数组或者字符串的连续子部分,这时候我们就可以考虑使用滑动窗口。nums[left,right] 为滑动窗口,根据具体的要求,通过遍历的时候,来改变 left 和right 的位置,从而完成任务。
滑动窗口主要用来处理连续问题,从类型上说主要有:
- 固定窗口大小
- 窗口大小不固定,求解最大的满足条件的窗口
- 窗口大小不固定,求解最小的满足条件的窗口
5.2真题分析
5.2.1滑动窗口最大值(239)
You are given an array of integers nums, there is a sliding window of size k which is moving from the very left of the array to the very right. You can only see the k numbers in the window. Each time the sliding window moves right by one position.
Return the max sliding window.

针对这种固定窗口大小的问题,一般思路是:我们同样固定初始化左右指针 l 和 r,分别表示的窗口的左右顶点。后面有所不同,我们需要保证:
1、l 和 r 都初始化为 0
2、r 指针移动一步
3、判断窗口内的连续元素是否满足题目限定的条件
3.1 如果满足,再判断是否需要更新最优解,如果需要则更新最优解。并尝试通过移动 l 指针缩小窗口大小。循环执行 3.1
3.2 如果不满足,则继续。
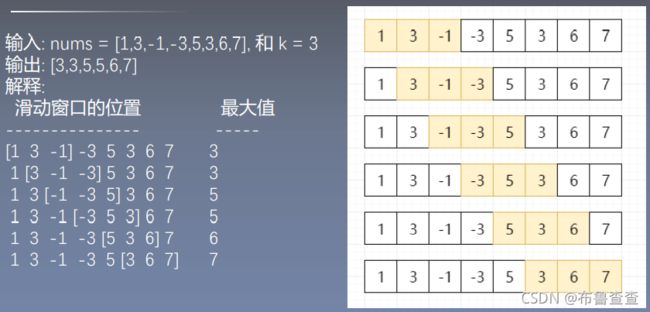
这题开始有点不好理解,可以看下图图示来理解:
#leetcode239
class Solution:
def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
##双指针的方式
res = []
L = 0
R = L+k
if len(nums)>0:
while R<len(nums)+1:
maxValue = max(nums[L:R])
res.append(maxValue)
L+=1
R+=1
return res
else:
return nums
5.2.2长度最小的子数组(209)
Given an array of positive integers nums and a positive integer target, return the minimal length of a contiguous subarray [numsl, numsl+1, ..., numsr-1, numsr] of which the sum is greater than or equal to target. If there is no such subarray, return 0 instead.

可变窗口也有一般思路:我们同样固定初始化左右指针 l 和 r,分别表示的窗口的左右顶点。后面有所不同,我们需要保证:
1、l 和 r 都初始化为 0
2、r 指针移动一步
3、判断窗口内的连续元素是否满足题目限定的条件
3.1 如果满足,再判断是否需要更新最优解,如果需要则更新最优解。并尝试通过移动 l 指针缩小窗口大小。循环执行 3.1
3.2 如果不满足,则继续。
针对此题,思路是:
1、开始 right 向右滑动,使和变大。
2、当恰好 >=s 时,记录滑窗所包括的子数组长度 res,若 res 已有数值,需判断新值是否小于旧值,若是,更新 res;left 向右滑动。
3、判断是否仍 >=s,若是,重复步骤 2,3。若否,转步骤 1。直到右边框到达最右边
#leetcode209
class Solution:
def minSubArrayLen(self, s: int, nums: List[int]) -> int:
# 初始化
left,sums,res = 0,0,float('inf')
# 右指针右移
for right in range(len(nums)):
sums += nums[right]
while sums >= s:
# 若新值小于旧值,更新res
if right - left + 1 < res:
res = right - left + 1
# 左指针向右滑动
sums -= nums[left]
left += 1
return 0 if res == float('inf') else res
5.2.3乘积小于K的子数组(713)
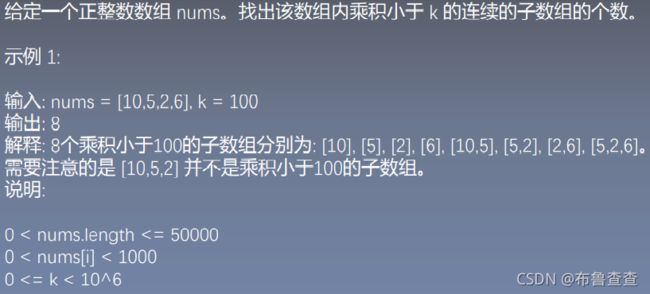
Given an array of integers nums and an integer k, return the number of contiguous subarrays where the product of all the elements in the subarray is strictly less than k.
思路:
步骤 1:当 left <= right 且滑动窗口内的乘积小于 k 时,我们可以知道 [left,right]、[left+1,right]…[right-1,right] 均满足条件,因此,计数加 right-left+1,然后移动右边界(滑动区间加大),看剩下的区间是否满足乘积小于 k,如果小于 k,重复步骤 1,否则进行步骤 2。
步骤 2:当滑动窗口内的乘积大于等于 k 时,右移左边界(滑动区间减小),如果这个区间内乘积小于 k,进入步骤 1,否则重复步骤 2。
#leetcode713
class Solution:
def numSubarrayProductLessThanK(self, nums: List[int], k: int) -> int:
left = 0
product = 1
count = 0
for right in range(len(nums)):
# 右边界右移
product *= nums[right]
# 如果乘积>=k,左边界右移
while left <= right and product >= k:
product /= nums[left]
left += 1
# 当前右边界下,满足条件的数组
count += right - left + 1
return count
6.分离双指针
6.1定义
输入是两个数组 / 链表,两个指针分别在两个容器中移动;根据问题的不同,初始位置可能都在头部,或者都在尾部,或一头一尾。
6.2真题分析
6.2.1两个数组的交集(350)
Given two integer arrays nums1 and nums2, return an array of their intersection. Each element in the result must appear as many times as it shows in both arrays and you may return the result in any order.

举个例子看通透一点,初始时两个指针分别在各自容器的头部,当所指的元素一样时,放到空列表里即可。
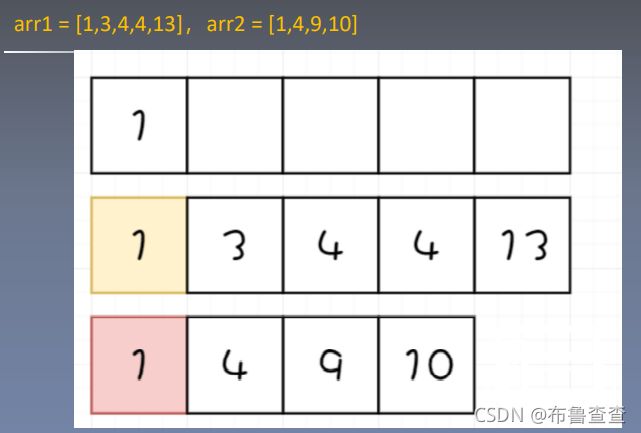
当所指元素不一样时,一个指针继续走下去,以此类推。元素较小的指针负责移动。
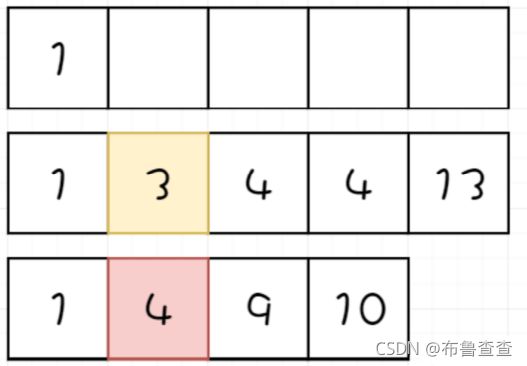

一路下去之后,想要的元素就都在存放结果的列表里了。
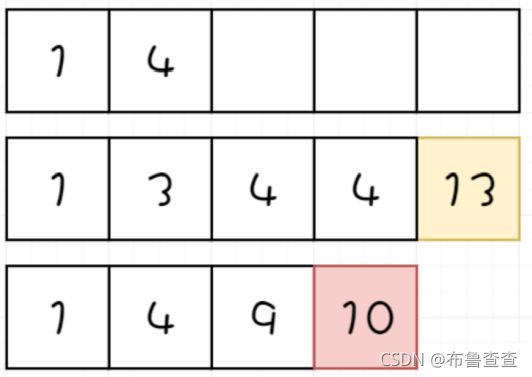
#leetcode350
class Solution:
def intersect(self, nums1: List[int], nums2: List[int]) -> List[int]:
# 排序
nums1.sort()
nums2.sort()
i,j = 0,0
res = []
while i < len(nums1) and j < len(nums2):
if nums1[i] > nums2[j]:
j += 1
elif nums1[i] < nums2[j]:
i += 1
elif nums1[i] == nums2[j]:
res.append(nums1[i])
i += 1
j += 1
return res
6.2.1两个数组的交集(349)
Given two integer arrays nums1 and nums2, return an array of their intersection. Each element in the result must be unique and you may return the result in any order.
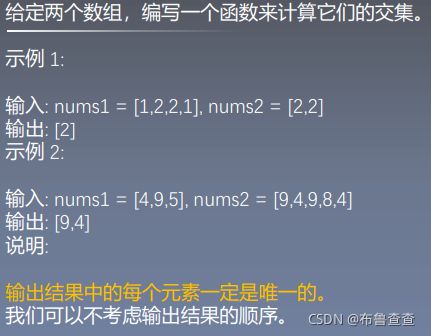
此题可以理解为350得出的结果,再查重一下,就可以得到每个元素都是唯一的了。再想一下,刚刚我们存放的是用列表list,那我们可以直接用集合set存放啊,这样就不会有重复元素啦。
#leetcode349
class Solution:
def intersection(self, nums1: List[int], nums2: List[int]) -> List[int]:
# 排序
nums1.sort()
nums2.sort()
i,j = 0,0
nums_set = set()#这里存放在了集合里了
while i < len(nums1) and j < len(nums2):
if nums1[i] > nums2[j]:
j += 1
elif nums1[i] < nums2[j]:
i += 1
elif nums1[i] == nums2[j]:
nums_set.add(nums1[i])
i += 1
j += 1
return nums_set
其实还有一个偷懒的方法,可以将两个数组转换成集合set,然后直接用python内置的交集。
class Solution:
def intersection(self, nums1: List[int], nums2: List[int]) -> List[int]:
set1 = set(nums1)
set2 = set(nums2)
return set1 & set2