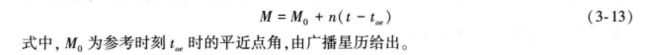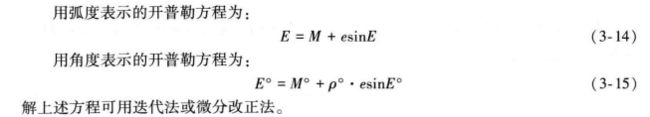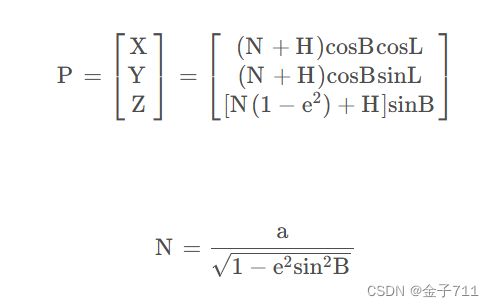DAY12---GINav学习

 1.调用关系图

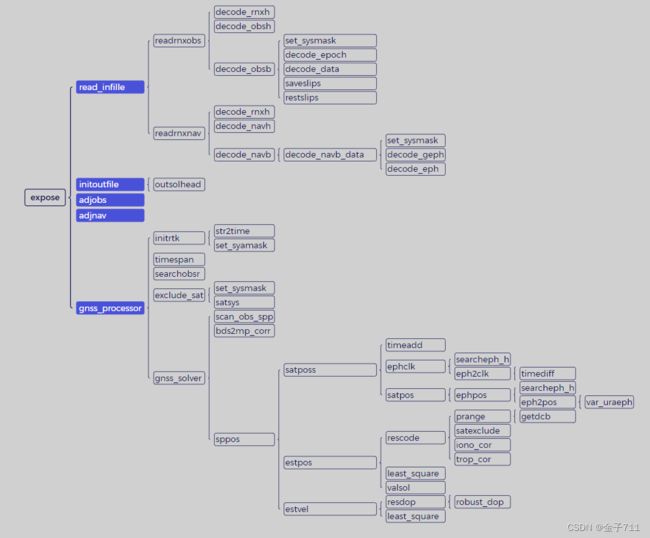
下图为GINav在matlab上进行标准单点定位的调用图，其中expose.m为入口。

 2.初始化输出

在进行初始化输出，调用initoutfile()函数，进行路径的设置，之后调用outsolhead（）函数，在该函数中主要输入软件的版本（GINav），读取用以生成结果文件表头中的开始时间、结束时间，数据处理的模式（SPP）、导航数据信息（系统的名字统计）、频率数量信息（1）、截至高度角（15°）、星历类型信息（broadcast）、电离层模型选择（broadcast model）、对流层模型选择（Saatamoinen model）、时间时的设置（GPST）、以及输出相应的速度信息与姿态信息。 

在进行spp的时候，主要进行下方代码。

%%根据时间输出选项 solopt.timef 的不同取值，确定时间的输出格式。
if solopt.timef==glc.SOLT_GPST
    str_time=sprintf('%s  %-12s%s','%','GPST',sep);%根据spp的时候输出的时间格式为GPST
elseif solopt.timef==glc.SOLT_UTC
    str_time=sprintf('%s  %-20s%s','%','UTC',sep);
else
    error('Time output options is wrong!!!');
end

%%根据位置输出选项 solopt.posf 的不同取值，确定位置的输出格式。
%%在进行spp的时候主要将以经纬度的形式输出坐标值
elseif solopt.posf==glc.SOLF_LLH
   str_pos=sprintf('%14s%s%14s%s%10s%s%3s%s%3s%s%8s%s%8s%s%8s%s%8s%s%8s%s%8s%s%6s%s%6s',...
                       'latitude(deg)',sep,'longitude(deg)',sep,'height(m)',sep,...
                       'Q',sep,'ns',sep,'sdn(m)',sep,'sde(m)',sep,'sdu(m)',sep,...
                       'sdne(m)',sep,'sdeu(m)',sep,'sdun(m)',sep,'age(s)',sep,'ratio');
    if solopt.outvel==1%速度
%%判断是否需要输出速度信息，如果 solopt.outvel 为 1，表示需要输出速度信息。
%%将速度输出格式化成字符串 str_vel，在进行spp的时候需要输出速度信息
        str_vel=sprintf('%s%10s%s%10s%s%10s%s%9s%s%8s%s%8s%s%8s%s%8s%s%8s',...
                        sep,'vn(m/s)',sep,'ve(m/s)',sep,'vu(m/s)',sep,'sdvn',sep,...
                        'sdve',sep,'sdvu',sep,'sdvne',sep,'sdveu',sep,'sdvun');
    end
else
    error('Position output options is wrong!!!');
end

上述代码为设置输出位置的格式，根据位置的类型，进而设置速度的格式。

if opt.ins.mode==glc.GIMODE_OFF%spp就进行这个，惯性导航系统关闭
    str=[str_time,str_pos];%先将时间信息与位置信息赋予str
    if ~strcmp(str_vel,'')%根据对应的坐标系统，选择相对应的速度，主要卫星在各个方向上进行偏移，导致各个方向的速度也会有所变化。如果速度为空，此时就不读取相应的速度信息。
        str=[str,str_vel];
    end
end

根据进行数据处理模式，选择的时SPP，此时惯性导航系统关闭，满足上述代码。str_time,str_pos与str_vel这三项结果，对时间信息，位置信息以及速度信息进行详细的输出。

 3.标准单点定位程序流程

从调用关系图可以看出，在进行标准单点定位时主要进行gnss_processor()函数，依次初始化一个RTK的结构、设置时间跨度（0-）、搜索接收机观测数据、排除不相关的接收机的观测数据和解决一个历元的gnss定位的问题。其中在进行单点定位的时候，发生在解决一个历元gnss定位里面。

3.1初始化一个RTK结构

function rtk=initrtk(rtk,opt)%定义一个initrtk（）函数，输入参数rtk与opt输出参数rtk

global glc%定义一个全局变量glc
rtk.opt=opt;%将opt的值赋予rtk.opt
rtk.opt.ts=str2time(rtk.opt.ts); %将str2time() 是一个用于将字符串形式的时间转换为时间戳的函数。
rtk.opt.te=str2time(rtk.opt.te);
rtk.mask=set_sysmask(opt.navsys);%设置卫星系统的掩码   

if opt.mode<=glc.PMODE_STATIC%选择的卫星系统数据处理的模式为spp，所以进行的是时候静态处理，所以满足以下选项。
    if opt.ionoopt==glc.IONOOPT_IFLC,NF=1;else,NF=opt.nf;end
%NO----IONOOPT_IFLC：使用无电离层组合观测量进行电离层延迟校正。
    if opt.dynamics==1,NP=9;else,NP=3;end%dynamics用以指定是否是动态定位模式，当然不是，此时NP=3（NP表示的是定位过程中估计的位置参数的数量）
    if opt.ionoopt==glc.IONOOPT_EST,NI=glc.MAXSAT;else,NI=0;end 
%NO-----IONOOPT_EST：估计电离层参数，并进行电离层延迟校正。
    if opt.tropopt

在该部分代码，主要设置模型的相关参数，位置参数、电离层延迟参数、对流层延迟参数等。得到相关的数据，将这些数量数据进行索引。

3.2设置时间跨度

function tspan=timespan(rtk,obsr)%定义了一个timespan（）函数，主要输入rtk与obsr参数，输出参数为tspan

conf_ts=rtk.opt.ts; conf_te=rtk.opt.te;%将rtk.opt.ts（开始时刻）与rtk.opt.te（结束时刻）的值分别赋予conf_ts与conf_te
obs_ts.time=obsr.data(1,1); %开始时间
obs_ts.sec=obsr.data(1,2);%开始秒
obs_te.time=obsr.data(end,1); %结束时间
obs_te.sec=obsr.data(end,2);%结束秒
dt=obsr.dt;%de表示的是接收机接收到的时间间隔

if conf_ts.time~=0&&timediff(conf_ts,obs_ts)>=0
    ts=conf_ts;
else
    ts=obs_ts;
end

if conf_te.time~=0&&timediff(conf_te,obs_te)<=0
    te=conf_te;
else
    te=obs_te;
end

tspan=fix(timediff(te,ts)/dt)+1;

return

接下来的 if 语句中，通过比较配置参数和观测时间点，选择合适的开始时间 ts。如果配置的开始时间不为0且与观测的开始时间相比是晚于等于的，那么 ts 就是配置的开始时间；否则， ts 为观测的开始时间。

类似地，第二个 if 语句选择合适的结束时间 te。如果配置的结束时间不为0且与观测的结束时间相比是早于等于的，那么 te 就是配置的结束时间；否则， te 为观测的结束时间。

最后，函数计算时间跨度，通过获取 te 和 ts 的时间差，并除以时间间隔 dt，然后取整得到一个表示跨度的整数值。加1是因为计算的是时间点个数。

在执行一个历元的时候，一般计算时间跨度，即一共需要多少个历元，以此为循环进行展开。

tspan=fix(timediff(te,ts)/dt)+1;

接收机在获取数据的时候，观测数据的时间间隔为30s，te表示的是开始的时间，ts表示的是结束的时间，fix（）函数用于向下取整，+1是因为计算的是时间点的个数，需要包括开始和结束时间点在内。

3.3搜索接收机观测数据与排除接收机不相关观测数据

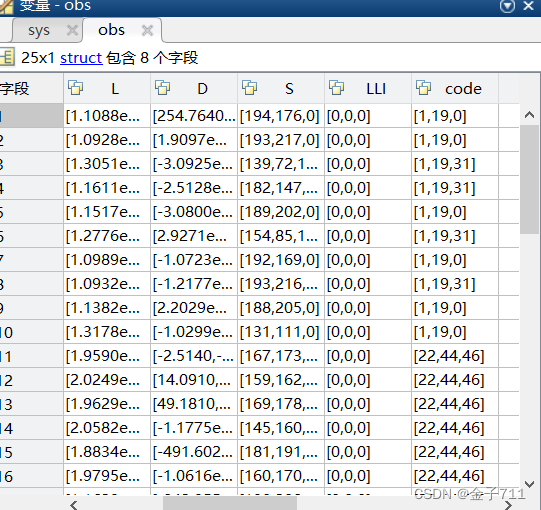
搜索接收机观测数据，该部分将相关的数据通过25次循环导入到obs里面。

obs=repmat(gls.obs_tmp,nobs,1);
for i=1:nobs%该部分主要循环25次
    obs(i).time.time=obs0(i,1);%将time.time复制为 obs0(i,1)----整数部分
    obs(i).time.sec=obs0(i,2);%将time.sec复制为 obs0(i,2)----小数部分
    obs(i).sat=obs0(i,3);%sat 被复制为 obs0(i,3)。----卫星编号
    obs(i).P=obs0(i,4:6);%P 被复制为 obs0(i,4:6)。----伪距测量值
    obs(i).L=obs0(i,7:9);%L 被复制为 obs0(i,7:9)。----载波相位测量值
    obs(i).D=obs0(i,10:12);%D 被复制为 obs0(i,10:12)。----多普勒测量值
    obs(i).S=obs0(i,13:15);%S 被复制为 obs0(i,13:15)。----信噪比
    obs(i).LLI=obs0(i,16:18);%LLI 被复制为 obs0(i,16:18)。----损失锁定指标
    obs(i).code=obs0(i,19:21);%code 被复制为 obs0(i,19:21)----码伪距测量值
end

排除接收机里面不相关的观测数据。

for i=1:nobs0
    
    time=obs0(i).time;
    %这是一个用于确定卫星的导航系统类型和卫星编号的函数。
    [sys,~]=satsys(obs0(i).sat);
    if mask(sys)==0,continue;end
    obs(nobs+1)=obs0(i);%进行25次循环，将obs里面的参数读取到obs（nobs+1）里面
    nobs=nobs+1;
end

 进行25次循环，每一次循环，读取一行的数据，一行中包括time、sat、P、L、D、S、ILI与code。

3.4解决一个历元gnss定位

    % solve an epoch%解决一个历元gnss定位的问题
    [rtk,~]=gnss_solver(rtk,obsr_,obsb_,nav);

3.4.1spp模式下扫描观测数据

该部分主要调用scan_obs_spp()函数。

    for f=1:glc.NFREQ
        dt=dt+obsr(i).P(f)*obsr(i).P(f);
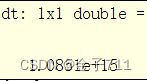
    end

glc.NFREQ表示的是频率的数量（3个），进行三次循环。时间间隔=上次时间间隔+第i个元素频率f的伪距观测值的平方。 这个i呢？主要跟那个nobs0有关，进行25次。进行之后dt结果如下所示。

3.4.2计算BDS2的多路径效应的修正

因为北斗卫星系统的复杂性，对于bds2多路径误差的计算主要是通过调用bds2mp_corr（）函数进行的。

3.4.3执行单点定位函数计算卫星相关参数

在该部分主要调用的是sppos（）函数。 

% defulat options for spp%设置进行spp的选择--这块不进行，因为已经是spp了
if rtk.opt.mode~=glc.PMODE_SPP
    opt.sateph =glc.EPHOPT_BRDC;%%1: 使用广播星历数据。GINav使用通过卫星广播信号传输的星历数据进行定位计算。
    opt.tropopt=glc.IONOOPT_BRDC;%%1: 使用广播电离层数据。GINav使用通过卫星广播信号传输的电离层数据进行电离层延迟的估计
    opt.ionoopt=glc.TROPOPT_SAAS;%%使用Saastamoinen模型。GINav使用Saastamoinen模型进行对流层延迟的估计。
end

（1）计算卫星位置、时钟偏差、速度

在该部分调用staposs（）函数。

时间计算公式：时间=上次时间+负的伪距观测值/光速值

具体代码如下所示。

time=timeadd(time0,-pr/glc.CLIGHT); %raw single transition
%%%glc.CLIGHT表示光速值
%%pr表示的是伪距观测值

 上式中的time表示的是发射时刻的时间，通过接收时刻的时间减去传播信号的时间得到的。

为什么要计算发射时刻的时间？

一：在进行卫星位置计算时，计算发射时刻的时间是为了考虑到信号的传播时间和接收机的接收时间。这是因为卫星的位置是在发射信号时确定的，但信号需要一定的时间才能从卫星传输到接收机。

二：计算发射时刻的时间可以帮助我们在接收到信号后，将信号的传播时间从总接收时间中减去，以获得更准确的卫星位置信息。这样可以更精确地进行卫星定位、导航和定位解算。

三：发射时刻的时间计算还可以用于校正时间方面的误差，例如卫星钟差、接收机钟差等，以确保接收到的信号时间与真实的发射时刻对齐。

总而言之，计算发射时刻的时间是为了纠正信号传播时间和减小定位误差，从而提高卫星定位的精度和准确性。

<1>卫星钟差计算：

首先是通过searcheph_h（）函数，能够在星历数据集中查找指定卫星在给定时间点的有效星历数据。该函数可能会使用一些特定的搜索算法或条件来筛选和匹配星历数据。

t0=abs(eph0(:,11)+eph0(:,12)-time.time-time.sec);
idx1=(t0<=tmax&t0<=tmin);
if ~any(idx1),eph_out=NaN;stat=0;return;end
t1=t0(idx1);
eph1=eph0(idx1,:);
idx2=t1==min(t1);
eph_=eph1(idx2,:);
eph2=eph_(end,:);

 代码段的功能是根据时间戳和条件筛选星历数据，并从中选择满足条件的最小时间差值对应的星历数据。

<2>钟差计算公式：钟差 = eph.f0 +eph.f1 * t +eph.f2 * t^2

• eph.f0 为卫星的零阶钟差补偿常数，表示卫星钟差在 t = 0 时刻的值。
• eph.f1 为卫星的一阶钟差补偿常数，表示卫星钟差对时间变化的线性响应。
• eph.f2 为卫星的二阶钟差补偿常数，表示卫星钟差对时间变化的二次响应。
• t 为观测时刻与卫星星历数据的参考时刻之间的时间差。

function t=eph2clk(time,eph)%eph2clk() 函数的具体功能是将星历数据（ephemeris）转换为卫星钟差（clock bias）。

t=timediff(time,eph.toc);
for i=1:3
    t=t-(eph.f0+eph.f1*t+eph.f2*t^2);%表示钟差的修正值
end

t=eph.f0+eph.f1*t+eph.f2*t^2;

return

<3>校正时间延迟(该部分校正相当于校正一个系统误差，设置阈值)

time=timeadd(time,-dts); %signal transition time

这行代码用于进行信号过渡时间的计算，其中 time 是输入的时间变量，dts 是信号过渡时间的参数。具体而言，这行代码调用了 timeadd() 函数来将 time 减去 dts，以获得信号过渡后的更新时间。

信号过渡时间是指信号在发送和接收之间的传输延迟。在接收信号时，由于信号需要一定的时间来传输，我们需要将接收时间提前一段适当的时间，以便与发送时间对应。

在进行卫星位置、钟差、速度的具体计算，主要调用satpos（）函数。

function [sv,stat]=satpos(time,obs,nav,ephopt,sv)%ephopt为1

global glc
teph=obs.time; sat=obs.sat;

switch ephopt
    case glc.EPHOPT_BRDC%%广播星历数据进行定位计算
        [sv,stat]=ephpos(time,teph,sat,nav,-1,sv); return;
    case glc.EPHOPT_PREC%%精密星历数据进行定位计算的选项
        [sv,stat]=peph2pos(time,sat,nav,1,sv); return;
    otherwise
        stat=0;return;
end

 在该部分的话switch ephopt的值为1，主要是使用扩展星历数据（如SBAS或SSR）进行定位计算在进行spp的时候，输入的文件为广播星历，所以只进行glc.EPHOPT_BRDC,选择广播星历数据进行卫星位置的计算。

在进行卫星位置计算的时候先调用ephpos（）函数，再调用eph2pos（）函数。

function [sv,stat0]=ephpos(time,teph,sat,nav,iode,sv) %#ok

global glc gls
stat0=1; tt=1e-3; sv1=gls.sv;
[sys,~]=satsys(sat);

if sys==glc.SYS_GPS||sys==glc.SYS_GAL||sys==glc.SYS_BDS||sys==glc.SYS_QZS%如果满足卫星系统的中的任何一项，就执行下面的内容。
%     [eph,stat]=searcheph(teph,sat,iode,nav);
    [eph,stat]=searcheph_h(teph,sat,-1,nav.eph);
%调用searcheph（）函数里面的。输入teph卫星的时间，卫星编号，-1，以及对应卫星的导航数据，输出参数为eph（卫星数据），stat（为状态，搜索执行状态，1 表示执行成功，0 表示执行失败）。
    if stat==0,stat0=0;return;end%----这一块就是执行失败，所以不允许该块。
    sv=eph2pos(time,eph,sv);
    time=timeadd(time,tt);%时间校正，校正传输过程中的误差（这部分属于系统误差）。
    sv1=eph2pos(time,eph,sv1);
    sv.svh=eph.svh;
end

通过广播星历计算卫星位置与速度，在该部分调用eph2pos（）函数。

 ①输入用于地球引力模型、地球角速度和开普勒方程的求解的多个参数

MU_GPS   =3.9860050E14;     % gravitational constant--GPS系统的地球引力常数         
MU_GAL   =3.986004418E14;   % earth gravitational constant--GAL系统的地球引力常数   
MU_BDS   =3.986004418E14;   % earth gravitational constant--BDS系统的地球引力常数  
OMGE_GAL =7.2921151467E-5;  % earth angular velocity (rad/s)---GAL系统的地球引力常数 
OMGE_BDS =7.292115E-5;      % earth angular velocity (rad/s)---BDS系统的地球角速度（弧度/秒）
RTOL_KEPLER =1E-13;         %开普勒方程求解的相对误差容限
MAX_ITER_KEPLER =30;        %开普勒方程求解的最大迭代次数
SIN_5 =-0.0871557427476582; % sin(-5.0 deg) %-5.0度的正弦值为-0.0871557427476582
COS_5  =0.9961946980917456; % cos(-5.0 deg) %-5.0度的正弦值为0.9961946980917456

 ②计算平近点角值M：

公式为M=eph.M0+(sqrt(mu/(eph.A*eph.A*eph.A))+eph.deln)*tk;

计算卫星运动的平均角速度n：

计算观测瞬间卫星的平近点角M：

 

 广播星历每2h更新一次，将参考时刻设在中央时刻，外推间隔小于等于1h，而卫星的运行周期为12h左右，采用卫星过近地点时刻来计算时，外推间隔最大有可能达6h，用参考时刻来取代卫星过近地点时刻后，外推间隔将大大减小，也能获得精度较高的结果。

M=eph.M0+(sqrt(mu/(eph.A*eph.A*eph.A))+eph.deln)*tk;

根据上述代码eph.M0表示的 为t0时刻的平近点角，eph.deln表示的是根据卫星运动而进行的摄动改正数值， tk表示的是从参考时间到待计算时间之间的时间间隔。

③计算卫星的偏近点角E：---开普勒方程

公式为E=E-(E-eph.e*sin(E)-M)/(1-eph.e*cos(E))

n=0; E=M; Ek=0;%%迭代求解开普勒方程
while abs(E-Ek)>RTOL_KEPLER&&n

abs(E-Ek)>RTOL_KEPLER&&nE 是当前偏近点角的值；Ek 是上一次迭代的偏近点角的值；RTOL_KEPLER 是用于判断迭代误差的阈值；n 是当前的迭代次数；MAX_ITER_KEPLER 是最大迭代次数的限制；eph.e：卫星的离心率；M：平近点角。终止条件可以是迭代次数达到最大值或者当前偏近点角与上一次迭代的偏近点角之差小于一个给定的阈值。

④计算真近点角、轨道半径与轨道倾角值

计算真近点角公式：u=atan2(sqrt(1.0-eph.e*eph.e)*sinE,cosE-eph.e)+eph.omg;

eph.e：轨道离心率；E：偏近点角；eph.omg：升交点赤经；eph.A：长半轴；eph.i0：初始轨道倾角；eph.idot：轨道倾角变化率。

计算轨道半径公式：r=eph.A*(1.0-eph.e*cosE); 

计算轨道倾角公式：i=eph.i0+eph.idot*tk; 

u=atan2(sqrt(1.0-eph.e*eph.e)*sinE,cosE-eph.e)+eph.omg;
r=eph.A*(1.0-eph.e*cosE); 
i=eph.i0+eph.idot*tk; 

⑤摄动改正后的真近点角、轨道半径与轨道倾角值

sin2u=sin(2.0*u); cos2u=cos(2.0*u);
u=u+eph.cus*sin2u+eph.cuc*cos2u; 
r=r+eph.crs*sin2u+eph.crc*cos2u; 
i=i+eph.cis*sin2u+eph.cic*cos2u; 
x=r*cos(u); y=r*sin(u); cosi=cos(i);

 上述的公式为计算摄动改正后的真近点角u、轨道半径r与轨道倾角值i，以及x与y值。

⑥计算坐标XYZ

 计算升交点赤经公式：O=eph.OMG0+(eph.OMGd-omge)*tk-omge*eph.toes

在上述公式中，  O 表示卫星在轨道上的升交点赤经；eph.OMG0 表示卫星的升交点赤经的初始值；

eph.OMGd 表示卫星的升交点赤经变化率；tk为时间差；omge为地球自转速度；eph.toes表示为星历的参考时间。

通过迭代更新升交点赤经，然后更新x、y与z值，将着三个值存储在rs里面。

    %%用于根据星历数据和其他轨道参数，更新卫星在轨道上的位置信息。
O=eph.OMG0+(eph.OMGd-omge)*tk-omge*eph.toes; 
    sinO=sin(O); cosO=cos(O);
    rs=[x*cosO-y*cosi*sinO; 
        x*sinO+y*cosi*cosO;
        y*sin(i)];

⑦计算与卫星钟差和观测误差

tk=timediff(time,eph.toc);
dts=eph.f0+eph.f1*tk+eph.f2*tk*tk;
dts=dts-2*sqrt(mu*eph.A)*eph.e*sinE/(glc.CLIGHT)^2;
%tk 表示观测时间与星历的参考时间之间的时间差，单位为秒。
%time 表示观测的时间戳。
%eph.toc 表示星历的参考时间，即星历的观测时间。
%dts 是卫星钟差校正项。
%eph.f0、eph.f1 和 eph.f2 是卫星钟差的校正参数。
%mu 是地球的引力常数。
%eph.A 是卫星轨道的半长轴。
%eph.e 是卫星轨道的离心率。
%sinE 是椭圆轨道中的偏近点角的正弦值。
%glc.CLIGHT 是光速。

在上述代码中进行两次卫星钟差的改正，改正后的钟差值为dts。 

计算观测误差（方差）：

ura_value=[2.4,3.4,4.85,6.85,9.65,13.65,24.0,48.0,96.0,192.0,384.0,768.0,1536.0,3072.0,6144.0];
ura=ura-1;
var=ura_value(ura+1)^2;

上述代码中ura代表用户距离精度（User Range Accuracy），它是一种用于描述卫星精度的参数。URA通常与GNSS定位中的卫星观测值（伪距或载波相位）相关联。其值越小，表示该卫星的距离测量精度越高，反之则越低，URA值主要用于确定GNSS定位中卫星观测数据的权重或方差。较低的URA值意味着更精确的测量，因此在GNSS定位算法中被赋予更高的权重，对定位结果的影响更大。而较高的URA值说明该卫星的测量结果可能有较大的不确定性，因此在定位算法中被赋予较低的权重。

sv.pos=rs;
sv.dts=dts;
sv.vars=vars;  

在该部分，主要将计算出来xyz值赋予sv.pos；钟差值dts赋予sv.dts；观测误差值vars赋予sv.vars。 

⑧计算卫星速度变化率

sv.vel=(sv1.pos-sv.pos)/tt;

sv.vel 表示卫星的速度向量；sv1.pos 表示卫星在时间 tt 之后的位置；sv.pos 表示卫星的当前位置；tt 表示时间差，用于计算位置和速度的变化率；sv.dtsd 表示卫星钟差的速度。

sv.vel=(sv1.pos-sv.pos)/tt;，可以计算出卫星的速度向量。它是通过卫星在时间差 tt 后的位置与当前位置之差，再除以时间差 tt 得到的。

⑨计算卫星钟差速度变化率

sv.dtsd=(sv1.dts-sv.dts)/tt

 sv.dtsd 表示卫星钟差的速度变化率；sv1.dts 表示卫星在时间 tt 之后的钟差；sv.dts 表示卫星的当前钟差；tt 表示时间差，用于计算钟差的速度变化率。

sv.dtsd=(sv1.dts-sv.dts)/tt;，可以计算出卫星钟差的速度变化率。它是通过卫星在时间差 tt 后的钟差与当前钟差之差，再除以时间差 tt 得到的。

（2）计算接收机的位置、钟差

在该部分调用estpos（）函数

①计算残差、测量模型和权重矩阵

在该部分调用的

是rescode（）函数。

 [v,H,P,vsat,azel,resp,nv,ns]=rescode(iter,obs,nav,sv,xr0,opt)
 %残差 v、设计矩阵 H、协方差矩阵 P、可见卫星数 ns、有效卫星数 nv

<1>坐标系转换（BLH---->XYZ）

地心地固坐标系转换为大地经纬度坐标系

while abs(z-zk)>1E-4
    zk=z;
    sinp=z/sqrt(r2+z*z);
    v=RE_WGS84/sqrt(1.0-e2*sinp*sinp);
    z=r(3)+v*e2*sinp;
end

if r2>1E-12
    pos(1)=atan(z/sqrt(r2));
    pos(2)=atan2(r(2),r(1));
else
    if r(3)>0
        pos(1)=pi/2;
    else
        pos(1)=-pi/2;
    end
    pos(2)=0;
end
pos(3)=sqrt(r2+z*z)-v;

将 pos=ecef2pos(rr);：调用 ecef2pos 函数，并将rr向量作为参数传入。这个函数的作用是将以地心地固坐标系表示的位置转换为经纬度坐标系中的位置。

伪距编码偏差校正

    [pr,Vmea]=prange(obs(i),nav,opt,azel(i,:),iter);
    if pr==0,continue;end
    if abs(pr)<1e7||abs(pr)>5e7,continue;end

 码偏差校正：将获得的码偏差估计值应用于伪距观测值，以校正由于码偏差引起的误差。校正过程将对每个卫星的伪距观测值进行调整，以减小码偏差带来的影响。

排除不必要卫星

 stat=satexclude(obs(i).sat,Vars,sv(i).svh,opt);

 计算电离层延迟

该部分调用iono_cor（）函数，在进行计算电离层延迟的时候使用的是Klobuchar模型：Klobuchar模型是一种由全球卫星导航系统（GNSS）提供的电离层延迟模型。该模型基于GNSS卫星的导航电文消息中包含的参数，如电离层的全球电离层地形模型（Global Ionospheric Maps，GIM）数据和对流层延迟查找表等，用于估计电离层延迟。

    iono_err=iono_klbc(time,pos,azel,nav.ion_gps);
    iono_var=(0.5*iono_err).^2;

 time：时间信息，用于观测电离层延迟的时间点；pos：接收机的位置信息，用于确定接收机的地理位置坐标；azel：接收机的方位角和仰角信息，用于指定接收机的指向；nav.ion_gps：导航数据中包含的GPS系统的电离层参数。

iono_err的计算：iono_err = iono_klbc(time, pos, azel, nav.ion_gps)：调用iono_klbc函数，根据给定的时间、位置、方位角和仰角以及GPS电离层参数，计算电离层的误差（iono_err）。

iono_var的计算：iono_var = (0.5 * iono_err).^2：将电离层误差的一半（0.5 * iono_err）进行平方运算得到电离层误差的方差（iono_var）。

计算对流层延迟

该部分调用trop_cor（）函数，在进行对流层延迟的时候使用的是Saastamoinen模型：这是最常用的对流层延迟模型之一。Saastamoinen模型基于大气湿度和温度分布，通过计算信号在对流层中传播时的路径长度以及折射率差异来估计对流层延迟的大小。

elseif opt==glc.TROPOPT_SAAS %Saastamoinen model
    trop_err=trop_saa(pos,azel,0.7); %humi=0.7
    trop_var=(0.3./(sin(azel(2))+0.1)).^2;
else

 trop_err的计算：trop_err = trop_saa(pos, azel, 0.7)：调用trop_saa函数，根据接收机的位置信息（pos）、方位角和仰角（azel）以及相对湿度（0.7），计算对流层误差（trop_err）。Saastamoinen模型是一种经典的对流层延迟模型，用于估计卫星信号传播过程中由于大气折射引起的延迟。

trop_var的计算：trop_var = (0.3./(sin(azel(2))+0.1)).^2：该式子计算了对流层误差的方差（trop_var）。这里使用了方位角和仰角（azel）来确定对流层延迟方差的大小，具体计算是将0.3除以（仰角的正弦值加上0.1），然后对结果进行平方。

伪距残差

 % 伪距残差
    v(nv+1)=pr-(r+dtr-glc.CLIGHT*dts+ionoerr+troperr);

代码的目的是通过将伪距观测值和相关修正项（钟差、电离层延迟、对流层延迟等）相减，计算出伪距的残差（观测值与预测值之间的差异）。这个残差可以用于定位算法中的伪距残差最小化问题，以提高GNSS定位的精度。

伪距残差（pseudo-range residual）的观测矩阵H（H矩阵）

H(nv+1,:)=[-LOS,1,0,0,0,0];
    if     sys==glc.SYS_GLO,v(nv+1)=v(nv+1)-x0(5);H(nv+1,5)=1;mask(2)=1;
    elseif sys==glc.SYS_GAL,v(nv+1)=v(nv+1)-x0(6);H(nv+1,6)=1;mask(3)=1;
    elseif sys==glc.SYS_BDS,v(nv+1)=v(nv+1)-x0(7);H(nv+1,7)=1;mask(4)=1;
    elseif sys==glc.SYS_QZS,v(nv+1)=v(nv+1)-x0(8);H(nv+1,8)=1;mask(5)=1;
    else                   ,                                  mask(1)=1;
    end

上述代码是根据系统类型，在H矩阵中更新相应的行、列和伪距残差，以及mask向量中的元素。这些更新是为了在定位算法中准确地建立观测矩阵和伪距残差方程，以进一步进行GNSS定位。

方差矩阵

在该代码中调用的是varerr_spp（）函数。

varr=opt.err(1)^2*(opt.err(2)^2+opt.err(3)^2/sin(el));%opt.err(1)：表示观测误差的第一个元素。；opt.err(2)：表示观测误差的第二个元素；opt.err(3)：表示观测误差的第三个元素；el：方位角和仰角的仰角分量；varr：观测误差的方差。
var=fact^2*varr;%fact：表示一个系数或缩放因子。

    VARr=varerr_spp(opt,azel(i,2),sys);
    var(nv+1,nv+1)=VARr+Vars+Viono+Vtrop+Vmea;

VARr：表示接收机单点定位误差的方差（variance）。这个方差根据函数varerr_spp()的调用和其他参数进行计算。var：表示方差矩阵、(nv+1, nv+1)：表示方差矩阵var的第(nv+1, nv+1)个元素，也就是方阵中的对角线元素。

上述代码的目的是将VARr（接收机单点定位误差的方差）与Vars（状态估计误差的方差）、Viono（电离层延迟误差的方差）、Vtrop（对流层延迟误差的方差）和Vmea（观测噪声的方差）相加，并将其结果赋值给方差矩阵var的对角线元素(var(nv+1, nv+1))。

记录和验证卫星观测数据以及对残差进行分析

   vsat(i)=1;  resp(i)=v(nv+1,1);  idx(nv+1)=i;

vsat(i)=1：将变量vsat的第i个元素赋值为1。通常用于表示第i个卫星的可见性，1表示可见，0表示不可见；resp(i)=v(nv+1,1)：将变量resp的第i个元素赋值为v的第(nv+1,1)个元素的值。变量v可能是一个数组或矩阵，而resp可能是记录相应响应值的变量；idx(nv+1)=i：将变量idx的第(nv+1)个元素赋值为i。变量idx通常用于存储索引或标识符，此处用于记录对应数据或状态的索引。

权重矩阵

for i=1:nv
    P(i,i)=var(i,i)^-1;
end

这段代码的含义是将协方差矩阵（var）的对角线元素的倒数赋值给P矩阵的对角线元素。具体解释如下，for i=1:nv：通过循环迭代变量i的值从1到nv，用于遍历协方差矩阵的对角线；P(i,i)=var(i,i)^-1：将P矩阵的第(i,i)个元素赋值为协方差矩阵var中对应位置元素的倒数。这里的var矩阵可能表示GNSS定位中的观测噪声协方差矩阵，P矩阵一般表示卡尔曼滤波中的状态估计协方差矩阵。将协方差矩阵的对角线元素的倒数赋值给P矩阵的对角线元素是为了计算状态估计值的权重，权重的倒数与协方差成正比。

该代码的目的是根据协方差矩阵的对角线元素，计算状态估计协方差矩阵P的逆。这在卡尔曼滤波等应用中非常常见，通过计算逆矩阵或伪逆可以获得状态变量的权重，进而影响状态估计的精度和可靠性。

②最小二乘法

function [x,VAR]=least_square(v,H,P)

%normal vector
N = (H'*P*H);%N = (H'*P*H);：计算法方程的normal matrix，即 H 矩阵的转置乘以观测协方差矩阵 P 再乘以 H 矩阵。


%cumpute unknown parameter
x = (N^-1)*H'*P*v;%根据最小二乘法的思想，计算未知参数的估计值 x。这里通过将法方程进行求逆，然后与 H 矩阵的转置乘以观测协方差矩阵 P 再乘以观测量 v 相乘来得到参数估计值。

%convariance of parameter
VAR = N^-1;%计算参数的协方差矩阵，即法方程的逆矩阵。这里直接将法方程的逆矩阵作为参数的协方差矩阵。

return

使用最小二乘法可以优化参数，通过最小化观测数据与参数估计值之间的残差平方和，找到最优的参数估计解，以此得到优化后的增量dx和参数的协方差矩阵Q。

（3）计算接收机的速度

①残差、测量模型和权重矩阵

在进行该块的时候调用的是resdop（）函数。  

    [v,H,P,nv]=resdop(rtk,obs,nav,sv,sat_,x);

    在地心地固坐标系中卫星速度相对于接收机的速度 

 delta_v=vs-x(1:3);

主要是计算两个速度向量之间的差异 

地球自转修正的测距速率 

   rate=dot(delta_v,e)+glc.OMGE/glc.CLIGHT*(vs(2)*rr(1)+rs(2)*x(1)-vs(1)*rr(2)-rs(1)*x(2));

 计算DOP残差值

v(nv+1,1)=-lam*dop-(rate+x(4)-glc.CLIGHT*dts_drift);

 设计测量模型

H(nv+1,:)=[-e',1];

计算方差 

    var(nv+1,nv+1)=DOP_VAR;

计算权重矩阵 

for i=1:nv
    P(i,i)=var(i,i)^-1;
end

 排除明显的错误（提升稳定性）

在此时调用robust_dop（）函数。

for i=1:nv0
    vi=abs(v0(i));
    if vi

 第一段代码将根据平均值和距离差异来决定哪些数据点将被标记为异常点。

第二段代码则将不是异常点的数据点存储到新的向量和矩阵中。

②最小二乘法

在该部分调用的是least_square()函数。 

[dx,~]=least_square(v,H,P);%v: 这是一个向量，包含观测值；H: 这是一个矩阵，包含设计测量矩阵与观测方程；P: 这是一个矩阵，包含观测噪声的协方差矩阵。

 在该部分中dx表示的是经过最小二乘法改正后的结果值。

function [x,VAR]=least_square(v,H,P)

%normal vector
N = (H'*P*H);%N = (H'*P*H);：计算法方程的normal matrix，即 H 矩阵的转置乘以观测协方差矩阵 P 再乘以 H 矩阵。


%cumpute unknown parameter
x = (N^-1)*H'*P*v;%根据最小二乘法的思想，计算未知参数的估计值 x。这里通过将法方程进行求逆，然后与 H 矩阵的转置乘以观测协方差矩阵 P 再乘以观测量 v 相乘来得到参数估计值。

%convariance of parameter
VAR = N^-1;%计算参数的协方差矩阵，即法方程的逆矩阵。这里直接将法方程的逆矩阵作为参数的协方差矩阵。

return

使用最小二乘法可以优化参数，通过最小化观测数据与参数估计值之间的残差平方和，找到最优的参数估计解，以此得到优化后的dx。

（4）检查位置和速度的一致性

（5）检查接收机钟差估计的正确性（是否正确与可靠）

3.4.4时间格式转换