2017EDSR

概要

该文开发了一种增强的深度超分辨率网络(EDSR)，其性能超过了目前最先进的SR方法。其的模型的显著性能改进是通过去除传统残差网络中不必要的模块（Batch Normalization）进行优化。在稳定训练（Residual Scaling）过程的同时，通过扩大模型尺寸进一步提高了性能。该文还提出了一种新的多尺度深度超分辨率系统(MDSR)和训练方法，该方法可以在单一模型中重建不同放大因子的高分辨率图像。

1. 背景

最近，深度神经网络在SR问题中在峰值信号调比(PSNR)方面提供了显著的性能。然而，这种网络在架构最优性方面表现出了局限性。首先，神经网络模型的重建性能对微小的结构变化很敏感。同样，同一模型通过不同的初始化会得到不同水平的性能。其次，现有的SR算法将不同尺度因子的超分辨率视为独立问题，没有考虑和利用不同尺度之间的相互关系，这些算法需要许多特定尺度的网络，需要独立训练来处理不同尺度。

使用多尺度训练VDSR模型可以显著提高性能，并优于特定尺度训练，这意味着特定尺度模型之间存在冗余性或者说可以利用不同尺度的信息来进行超分研究。尽管如此，VDSR的结构需要双边插值图像作为输入，与具有特定尺度的上采样方法的架构相比，这导致了更重的计算时间和内存。

2. 结构

2.1 Enhanced Residual Network

近年来，残差网络在从低级到高级任务的计算机视觉问题中表现出优异的性能。虽然Ledig等人成功地将ResNet架构应用于SRResNet的超分辨率问题，但我们通过采用更好的ResNet结构进一步提高了性能。

在图2中，我们比较了来自原始ResNet、SRResNet和我们提出的网络的每个网络模型的构建块。如Nah等人在他们的图像去模糊工作中所述，我们从我们的网络中删除了批处理归一化层。

Batch Normalization的缺点：

• 由于批处理归一化层对特征进行了归一化，它们通过对特征进行归一化，消除了网络的范围灵活性，最好是去除它们。
• GPU内存使用也充分减少，因为批处理规范化层消耗与前面的卷积层相同的内存。与SRResNet相比，我们的没有批处理归一化层的基线模型在训练期间节省了大约40%的内存使用。因此，在有限的计算资源下，我们可以建立一个比传统ResNet结构性能更好的更大的模型。

2.2 Single-scale model

提高网络模型性能的最简单的方法是增加参数的数量。在卷积神经网络中，模型的性能可以通过堆叠多层或增加滤波器的数量来提高。具有深度（层数）B和宽度（特征通道数）F的一般CNN架构大约占用具有$O(B{F}^2)$的参数和$O(BF)$的内存。因此，在考虑有限的计算资源时，增加F而不是B可以使模型容量最大化。

然而，我们发现增加特征图的数量超过一定的水平会使训练过程在数值上不稳定。Szegedy等人的也报道了类似的现象。通过采用因子为0.1的残差尺度来解决这个问题。

我们用图2中提出的残差块构建了我们的基线（单尺度）模型。该结构类似于SRResNet，但我们的模型在残余块之外没有ReLU激活层。此外，我们的基线模型没有残差缩放层，因为我们为每个卷积层只使用64个特征映射。在我们最终的单尺度模型(EDSR)中，我们通过设置B=32，F=256来扩展基线模型。模型体系结构如图3所示

Train Process：

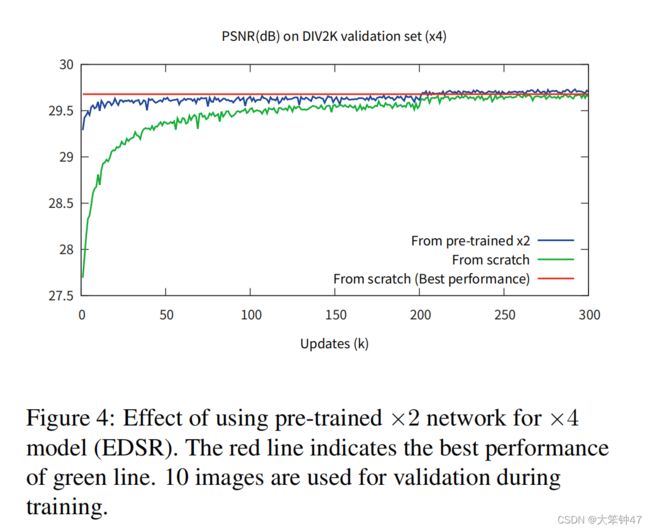
在训练的过程中，对于scale X2尺度的是从头开始训练，对于scale X4的训练，将采用scale X2的参数。

2.3 Multi-scale model

从图4的观察，我们得出多个尺度的超分辨率是相互关联的任务。我们可以像VDSR一样，通过构建一个利用尺度间相关性的多尺度体系结构，进一步探索了这一想法。我们设计了我们的基线（多尺度）模型，使其有一个单一的主分支与B=16剩余块，这样大多数参数在不同的尺度上共享，如下图所示：

在每次训练多尺度模型(MDSR)更新时，我们在×2、×3和×4中随机选择一个尺度构建小批量。只有与所选比例对应的模块才会被启用和更新。因此，与不同尺度以外的特定尺度剩余块对应的特定尺度剩余块和上采样模块不会启用或更新。

3. 训练参数

3.1 Loss 函数

我们用L1损失而不是L2来训练我们的网络。最小化L2通常是首选的，因为它能使PSNR最大化。然而，通过一系列的实验，我们发现L1损失比L2具有更好的收敛性。

3.2 Geometric Self-ensemble

有一个tip。为了最大化我们的模型的潜在性能，我们采用了的 self-ensemble strategy。在测试期间，我们通过翻转和旋转输入图像$I_{LR}$，为每个样本生成7个增强输入$I_{n,i}^{LR}=T_i(I_n^{LR})$；其中$T_i$代表包括自己的8个变换。利用这些增强的低分辨率图像，我们通过网络生成相应的超分辨率图像$\{I_{n,1}^{SR},...,I_{n,8}^{SR}\}$。然后，我们对这些输出的图像进行逆变换，得到原始的几何图形${\hat{I}}_{n,i}^{SR}=T_i^{-1}(I_{n,i}^{SR})$。最后，我们将转换后的输出一起平均：
$$I_n^{SR}=\frac{1}{8}\sum _{i=1}^8{\hat{I}}_{n,i}^{SR}$$
我们通过在方法名中添加$+$后缀来表示使用self-ensemble strategy，即$EDSR+/MDSR+$。

4. 结果

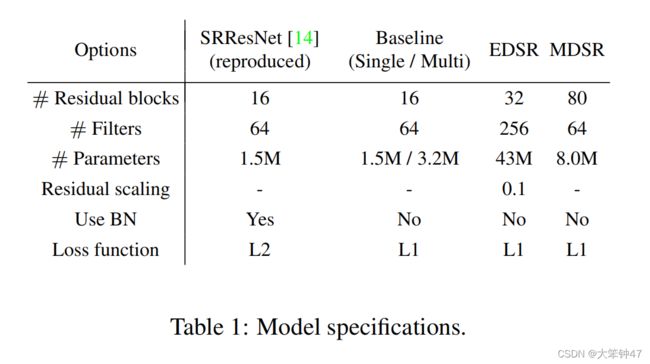
关于model的配置参数：

结果：

Reference：**Enhanced Deep Residual Networks for Single Image Super-Resolution