新城里的旧少年^_^

Leetcode dfs bfs 递归回溯题目

组合总和系列

Leetcode39 组合总和I

//这个由于组合方案不能重复，我们每次对第pos个位置的数，可以进行选0次，选1次...选k次的行为，来计算和
int n;
void dfs(int* candidates,int target,int** res,int *returnSize,int* path,int u,int sum,int** returnColumnSizes,int pos) //pos代表枚举到了哪个位置了
{
    if(sum == target){
        res[*returnSize] = malloc(sizeof(int)*1010);
        for(int i = 0; i < u; i++) res[*returnSize][i] = path[i];
        (*returnColumnSizes)[*returnSize] = u;
        (*returnSize)++;
        return;
    }
    if(pos == n) return;
    for(int k = 0; sum + k * candidates[pos] <= target; k++){
        if(k == 0) dfs(candidates,target,res,returnSize,path,u,sum,returnColumnSizes,pos+1);
        else{
            for(int i = 0; i < k; i++) path[u+i] = candidates[pos];
            dfs(candidates,target,res,returnSize,path,u+k,sum+k*candidates[pos],returnColumnSizes,pos+1); 
        }
    }
}

int** combinationSum(int* candidates, int candidatesSize, int target, int* returnSize, int** returnColumnSizes){
    n = candidatesSize;
    int** res = malloc(sizeof(int*)*1010);
    int* path = malloc(sizeof(int)*1010);
    (*returnColumnSizes) = malloc(sizeof(int)*1010);
    *returnSize = 0;
    dfs(candidates,target,res,returnSize,path,0,0,returnColumnSizes,0);
    return res;
}

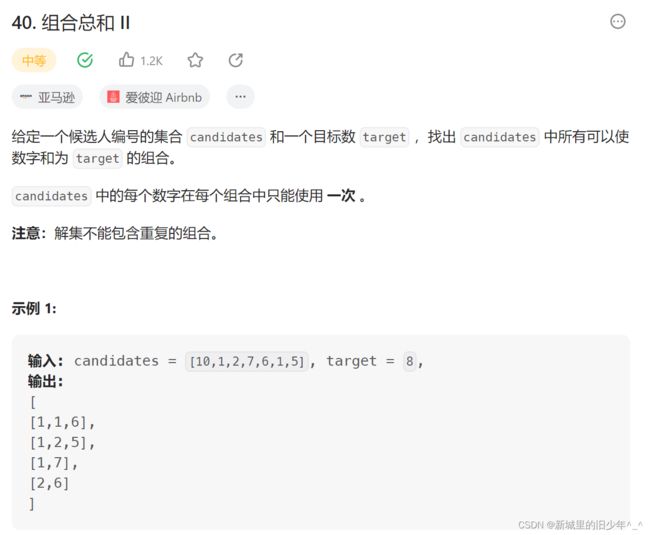
Leetcode40 组合总和II

这个题要求的是数组中的每个元素只能用1次，
然后组合不能有重复的，也就是说 1 1 2 3 target = 6
[1,2,3]这个只能出现一次，所以为了去重，需要对原数组进行从小到大的排序，当nums[i] == nums[i-1]但是nums[i-1]没被选用过时，我们不要用nums[i]这样来避免重复

int n;
int cmp(const void *a, const void* b)
{
    return *(int*)a - *(int*)b;
}
bool visit[1010];

void dfs(int* candidates,int n,int** res,int* returnSize,int** returnColumnSizes,int* path,int u,int pos,int sum,int target)
{
    if(sum == target){
        res[*returnSize] = malloc(sizeof(int)*1010);
        for(int i = 0; i < u; i++) res[*returnSize][i] = path[i];
        (*returnColumnSizes)[*returnSize] = u;
        (*returnSize)++;
        return;
    }
    if(sum > target) return;
    if(pos == n) return; //枚举了数组中的所有数但是没找到target的和的直接退出
    visit[pos] = 0;
    dfs(candidates,n,res,returnSize,returnColumnSizes,path,u,pos+1,sum,target);
    if(pos && candidates[pos-1] == candidates[pos] && !visit[pos-1]) return;
    path[u] = candidates[pos];
    visit[pos] = 1;
    dfs(candidates,n,res,returnSize,returnColumnSizes,path,u+1,pos+1,sum+candidates[pos],target);
}

int** combinationSum2(int* candidates, int candidatesSize, int target, int* returnSize, int** returnColumnSizes){
    n = candidatesSize;
    memset(visit,0,sizeof(visit));
    qsort(candidates,n,sizeof(candidates[0]),cmp);
    int** res = malloc(sizeof(int*)*1010);
    *returnSize = 0;
    (*returnColumnSizes) = malloc(sizeof(int)*1010);
    int* path = malloc(sizeof(int)*1010);
    dfs(candidates,n,res,returnSize,returnColumnSizes,path,0,0,0,target);
    
    return res;
}

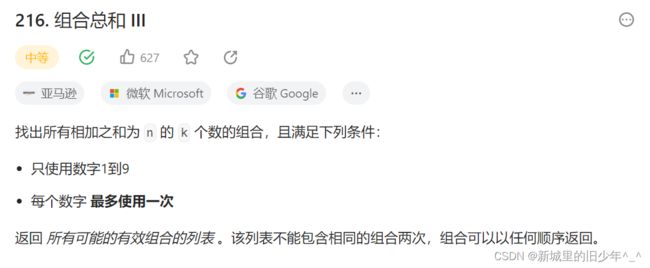
Leetcode216 组合总和III

void dfs(int** res,int* returnSize,int** returnColumnSizes,int* path,int u,int k,int n,int sum,int len,int pos)
{
    if(len > k) return;
    if(len == k){
        if(sum == n){
            res[*returnSize] = malloc(sizeof(int)*1010);
            for(int i = 0; i < u; i++) res[*returnSize][i] = path[i];
            (*returnColumnSizes)[*returnSize] = u;
            (*returnSize)++;
            return;
        }
    }
    if(pos > 9) return;
    dfs(res,returnSize,returnColumnSizes,path,u,k,n,sum,len,pos+1);
    path[u] = pos;
    dfs(res,returnSize,returnColumnSizes,path,u+1,k,n,sum+pos,len+1,pos+1);
}

int** combinationSum3(int k, int n, int* returnSize, int** returnColumnSizes){
    int** res = malloc(sizeof(int*)*1010);
    *returnSize = 0;
    (*returnColumnSizes) = malloc(sizeof(int)*1010);
    int* path = malloc(sizeof(int)*1010);
    dfs(res,returnSize,returnColumnSizes,path,0,k,n,0,0,1);
    return res;
}

Leetcode 377组合总和IV

//如果求方案种类，递归写法
int n;
void dfs(int* candidates,int target,int** res,int *returnSize,int* path,int u,int sum,int** returnColumnSizes)
{
    if(sum == target){
        res[*returnSize] = malloc(sizeof(int)*1010);
        for(int i = 0; i < u; i++) res[*returnSize][i] = path[i];
        (*returnColumnSizes)[*returnSize] = u;
        (*returnSize)++;
        return;
    }
    for(int i = 0; i < n; i++){
        if(sum + candidates[i] <= target){
            path[u] = candidates[i];
            dfs(candidates,target,res,returnSize,path,u+1,sum+candidates[i],returnColumnSizes);
        }
    }
}

int combinationSum4(int* nums, int numsSize, int target){
    int* returnSize = malloc(sizeof(int));
    int** returnColumnSizes = malloc(sizeof(int*));
    (*returnColumnSizes) = malloc(sizeof(int)*1010);
    int** res = malloc(sizeof(int*)*1010);
    int* path = malloc(sizeof(int)*1010);
    (*returnColumnSizes) = malloc(sizeof(int)*1010);
    n = numsSize;
    *returnSize = 0;
    dfs(nums,target,res,returnSize,path,0,0,returnColumnSizes);
    return *returnSize;
}

这题只求方案数，可以用动态规划做，
但是这个题还不是完全背包，完全背包会将顺序不同但是组合相同的算作前一种，比如 1 1 4 和 1 4 1是两种组合，但是完全背包会看作是一种组合

所以我们不要被背包模板所迷惑了，这个题直接考虑
$f [i]$ 表示 $i$ 的所有划分方案的集合数的最大值(比如 $i = 4$ ，那么 $f [4]$ 就是能够组合成4的所有可能的集合数)
$i$ 能够由若干数组合而来，比如a+b+c+…+ j = i
由于这个组合是考虑排列序列的，所以我们枚举组合成i的这个组合的最后一个数 $j$ ,这个 $j$ 可能是 $n u m s [0], n u m s [1], ..., n u m s [n - 1]$
那么组成i的集合最后一个数是j时就有 $f [i] = f [i - j]$
最后把所有可能的j加起来就是f[i]的结果

int combinationSum4(int* nums, int numsSize, int target){
    int n = numsSize, m = target;
    long long f[m+10]; //f[i]表示i这个值能被划分成的集合数
    memset(f,0,sizeof(f));
    f[0] = 1; //0这个数能被划分的集合数只有1个,那就是空集
    for(int i = 1; i <= m; i++){
        for(int j = 0; j < n; j++)
        {
            if(i>=nums[j]) f[i] = (f[i] + f[i-nums[j]])%INT_MAX;
            // if(i>=nums[j]) printf("%d %d\n",i,i-nums[j]);
        }
    }
    return f[m];
}

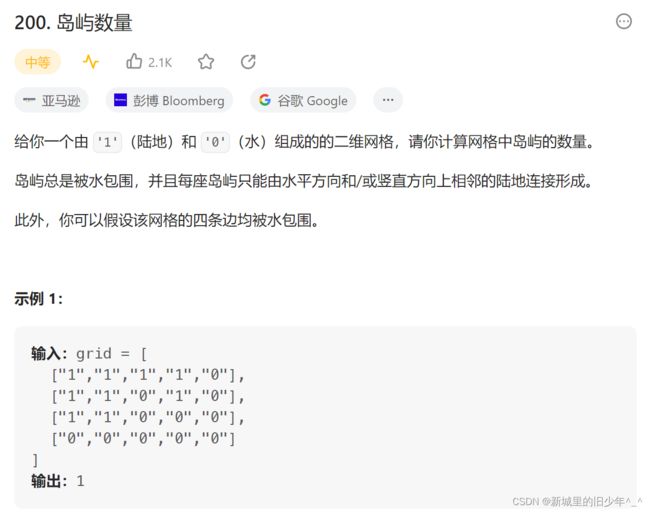
Leetcode200

int n,m;
int dx[4] = {0,0,1,-1},dy[4] = {1,-1,0,0};

void dfs(char** grid,int x,int y)
{
    if(x < 0 || x >= n || y < 0 || y >= m || grid[x][y] == '0') return;
    grid[x][y] = '0';
    for(int i = 0; i < 4; i++){
        int nx = x + dx[i],ny = y + dy[i];
        dfs(grid,nx,ny);
    }
}

int numIslands(char** grid, int gridSize, int* gridColSize){
    int res = 0;
    n = gridSize,m = gridColSize[0];
    for(int i = 0; i < n; i++){
        for(int j = 0; j < m; j++){
            if(grid[i][j] == '0') continue;
            res++;
            dfs(grid,i,j);
        }
    }
    return res;
}

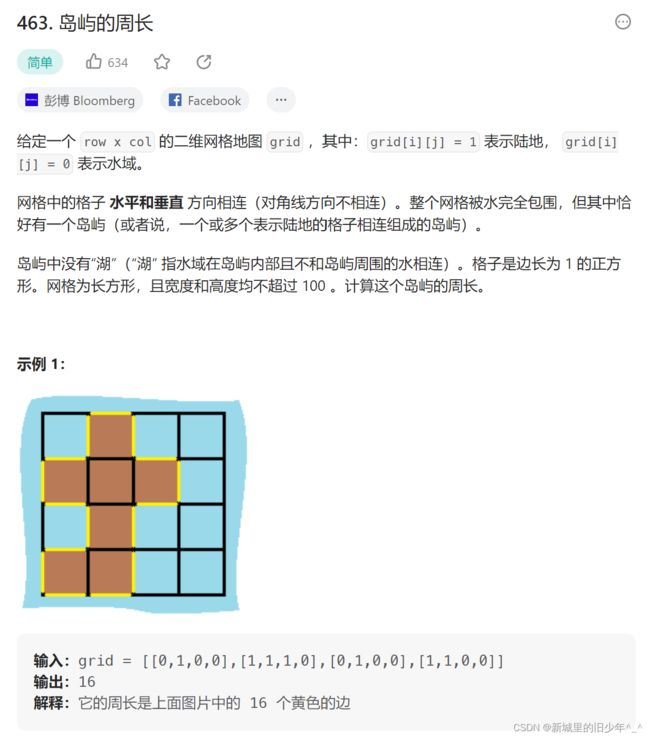
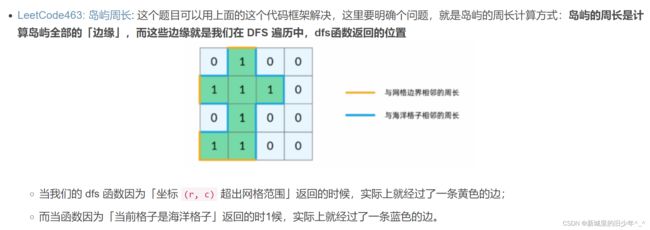
Leetcode463岛屿周长

非递归版本



int islandPerimeter(int** grid, int gridSize, int* gridColSize){
    int res = 0;
    int n = gridSize,m = gridColSize[0];
    int dx[4] = {0,0,1,-1},dy[4] = {1,-1,0,0};
    for(int i = 0; i < n; i++){
        for(int j = 0; j < m; j++){
            if(grid[i][j] == 0) continue;
            int cnt = 0; //从一个陆地块，看他四周的下一个块是不是越界或者是海洋
            for(int k = 0; k < 4; k++){
                int nx = i + dx[k],ny = j + dy[k];
                if(nx < 0 || nx >= n || ny < 0 || ny >= m || grid[nx][ny] == 0) cnt++;
            }
            res += cnt;
        }
    }
    return res;
}

递归版本

int dx[4] = {1,-1,0,0},dy[4] = {0,0,1,-1};
int dfs(int** grid,int n,int m,int x,int y)
{
    if(x < 0 || x>=n || y < 0 || y >= m || grid[x][y] == 0) return 1;
    if(grid[x][y] == 2) return 0; //如果这个陆地块被访问过，不再加入这个路地块开始遍历的值
    grid[x][y] = 2;
    int ans = 0;
    for(int i = 0; i < 4; i++){
        int nx = x + dx[i],ny = y + dy[i];
        ans += dfs(grid,n,m,nx,ny);
    }
    return ans;
}

int islandPerimeter(int** grid, int gridSize, int* gridColSize){
    int n = gridSize,m = gridColSize[0];
    int res = 0;
    for(int i = 0; i < n; i++){
        for(int j = 0; j < m; j++){
            if(!grid[i][j]) continue;
            res += dfs(grid,n,m,i,j);
        }
    }
    return res;
}

Leetcode695岛屿最大面积

//这个题是要求的是图中所有岛屿中有最大面积的那个岛屿
int max(int a,int b)
{
    return a>b?a:b;
}

int dx[4] = {0,0,1,-1},dy[4] = {1,-1,0,0};
int dfs(int** grid,int n,int m,int x,int y)
{
    if(x < 0 || x>=n || y<0 || y>=m || grid[x][y] == 0) return 0;
    int ans = 1;
    grid[x][y] = 0;
    for(int i = 0; i < 4; i++){
        int nx = x + dx[i],ny = y + dy[i];
        ans += dfs(grid,n,m,nx,ny);
    }
    return ans;
}

int maxAreaOfIsland(int** grid, int gridSize, int* gridColSize){
    int res = 0;  //leetcode这里如果把res写成全局变量，第二次调用时，res还是第一次的结果，所以要写到局部变量里
    int n = gridSize,m = gridColSize[0];
    for(int i = 0; i < n; i++){
        for(int j = 0; j < m; j++){
            if(grid[i][j] == 0){
                printf("yrs\n");
                continue;
            }
            int t = dfs(grid,n,m,i,j);
            res = max(res,t);
        }
    }
    printf("%d",res);
    return res;
}

Leetcode827最大人工岛

这道题用并查集做会更加的高效，对于并查集：

并查集核心思想：
int p[N]; //定义个parent数字，代表i号点的父亲是几号点
然后最开始所有 p[i] = i代表自己是一个集合
//定义核心函数int find(int x)
int find(int x)
{
    if(x!=p[x]) p[x] = find(p[x]);
    return p[x];
}

/***
基本思想：
首先将所有不联通的岛屿，构成一个个并查集，并且记录下每一个岛屿的面积
然后枚举每一个grid[i][j] = 0的点，然后看把这个点变为1后其上下左右是否有不同的与这个单独的快联通的并查集
然后把这几个并查集的面积加起来再加1就是新的联通块面积了
***/
int n,m;
int* p;    //定义i号节点的父节点
int* area;  //连通块面积
int dx[4] = {1,-1,0,0},dy[4] = {0,0,1,-1};

int max(int a,int b)
{
    return a>b?a:b;
}

int get(int a,int b)
{
    return a*m + b; //二维数组下标变一维的方法就是  行坐标*列数 + 纵坐标
}

int find(int x)    // 并查集核心函数，查找x号节点的父节点
{
    if(p[x] != x) p[x] = find(p[x]);
    return p[x];  
}

int largestIsland(int** grid, int gridSize, int* gridColSize){
    n = gridSize,m = gridColSize[0];
    int res = 0;
    p = malloc(sizeof(int)*1000000);
    area = malloc(sizeof(int)*1000010);

    for(int i = 0; i < n * m; i++){  //并查集初始化
        p[i] = i;
        area[i] = 1;
    }
    
    for(int i = 0; i < n; i++){
        for(int j = 0; j < m; j++){
            if(grid[i][j]){
                int a = get(i,j); //(i,j)所属的并查集编号
                for(int k = 0; k < 4; k++){
                    int nx = i + dx[k],ny = j + dy[k];
                    if(nx>=0 && nx<n && ny>=0 && ny<m && grid[nx][ny]){
                        int b = get(nx,ny);
                        if(find(a) != find(b)){
                            area[find(b)] += area[find(a)];
                            p[find(a)] = find(b);
                        }
                    }
                }
                res = max(res,area[find(a)]);
            }
        }
    }
    for(int i = 0; i < n; i++){
        for(int j = 0; j < n; j++){
            if(!grid[i][j]){
                int hash[1000010];
                memset(hash,0,sizeof(hash));
                int s = 1;
                for(int k = 0; k < 4; k++){
                    int nx = i + dx[k],ny = j + dy[k];
                    if(nx>=0 && nx<n && ny>=0 && ny<m && grid[nx][ny]){
                        int a = get(nx,ny);
                        if(!hash[find(a)]){
                            hash[find(a)] = area[find(a)];
                            s += area[find(a)];
                        }
                    }
                }
                res = max(res,s);
            }
        }
    }
    return res;
}

Leetcode542 01矩阵

Leetcode241为算数表达式设置优先级

int* dfs(char* s,int l,int r,int *returnSize)
{
    if(l > r){
        int* res = malloc(sizeof(int)*10);
        *returnSize = 0;
        return res;
    }
    int *res = malloc(sizeof(int)*10100);
    *returnSize = 0;
    for(int i = l ; i <= r; i++){
        if(s[i]>='0' && s[i]<='9') continue; //是数字的时候直接过
        //此时s[i]= + - * 中的一种
        int* leftsize = malloc(sizeof(int));
        int* rightsize = malloc(sizeof(int));
        int* left = dfs(s,l,i-1,leftsize);
        int* right = dfs(s,i+1,r,rightsize);
        for(int j = 0; j < *leftsize; j++){
            for(int k = 0; k < *rightsize; k++){
                int t = 1;
                if(s[i] == '+') t = left[j] + right[k];
                else if(s[i] == '-') t = left[j] - right[k];
                else if(s[i] == '*') t = left[j] * right[k];
                res[*returnSize] = t;
                (*returnSize)++;
            }
        }
    }
    if(*returnSize == 0){//说明这一段的字符只有数字没有运算符
        int ans = 0;
        for(int i = l; i <= r; i++) ans = ans * 10 + s[i] - '0';
        res[*returnSize] = ans;
        (*returnSize)++;
    }
    return res;
}
int* diffWaysToCompute(char * expression, int* returnSize){
    int n = strlen(expression);
    return dfs(expression,0,n-1,returnSize);
}

Leetcode698划分为k个等和子集

这题和那个拼火柴的基本是一个题，拼火柴是把数组拼成4条边，这个是把数组拼成k条边

//和火柴一个做法，几乎能AC所以的
int cmp(const void* a,const void* b)
{
    int* aa = (int*)a;
    int* bb = (int*)b;
    if(*aa < *bb) return 1;
    return -1;
}

bool dfs(int* board,int* nums,int n,int u,int len,int k)
{
    bool flag = true;
    for(int i = 0; i < k; i++){
        if(board[i] != len){
            flag = false;
            break;
        }
    }
    if(flag) return true; //如果k段都已经设置为了长度len,那么能找到方案
    if(u >= n) return false; //找遍数组还没找到答案
    for(int i = 0; i < k; i++){
        if(board[i] + nums[u] > len) continue;
        board[i] += nums[u];
        if(dfs(board,nums,n,u+1,len,k)) return true;
        board[i] -= nums[u];
    }
    return false;
}

bool canPartitionKSubsets(int* nums, int n, int k){
    int sum = 0;
    for(int i = 0; i < n; i++) sum += nums[i];
    if(sum % k) return false; //总和不是k的倍数，说明不可能划分为k段
    int len = sum / k; //若能够划分为k段，则每段的长度为 sum / k
    qsort(nums,n,sizeof(nums[0]),cmp);
    if(nums[0] > len) return false;
    int* board = malloc(sizeof(int)*(k+10)); //board[i]记录每一段已经放了多长
    for(int i = 0; i < k; i++) board[i] = 0;
    return dfs(board,nums,n,0,len,k);
}

Leetcode473火柴拼正方形

int cmp(const void* a,const void* b)
{
    int* aa = (int*)a;
    int* bb = (int*)b;
    if(*aa < *bb) return  1;
    return -1;
}

bool dfs(int* board,int len,int* nums,int n,int u) //u代表枚举到nums中的哪一个位置了
{
    if(board[0] == len && board[1] == len && board[2] == len && board[3] == len) return true; 
    if(u == n) return false; //如果遍历没了还没找到答案，一定是错的(因为来到这个if就是上面那个成功条件没满足)
    for(int i = 0; i < 4; i++){//把当前这个火柴分别放到4个边上
        if(board[i] + nums[u] > len) continue;
        board[i] += nums[u];
        if(dfs(board,len,nums,n,u+1)) return true;
        board[i] -= nums[u];
    }
    return false;
}

bool makesquare(int* matchsticks, int matchsticksSize){
    int n = matchsticksSize;
    if(n < 3) return false; //小于3根不可能拼成正方形
    int sum = 0;
    for(int i = 0; i < n; i++) sum += matchsticks[i];
    if(sum%4!=0) return false; //如果长度总和不是4的倍数，那么直接退出
    int len = sum / 4; //正方形每个边的长度
    qsort(matchsticks,n,sizeof(matchsticks[0]),cmp); //从大到小排序，先枚举大的
    for(int i = 0; i < n; i++){
        if(matchsticks[i] > len) return false; //如果最长的边超过了可能拼成的正方形边长，直接退出
    }
    int* board = malloc(sizeof(int)*8); //board记录正方形4个边的每个边已经枚举了多长了
    for(int i = 0; i < 4; i++) board[i] = 0;
    return dfs(board,len,matchsticks,n,0);
}

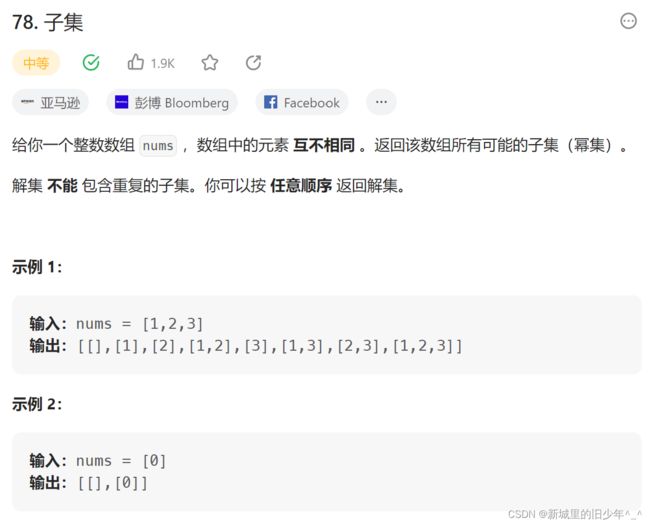
Leetcode78子集

/**
 * Return an array of arrays of size *returnSize.
 * The sizes of the arrays are returned as *returnColumnSizes array.
 * Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().
 */
int* visit;
int** res;


void dfs(int* returnSize,int* nums,int n,int** returnColumnSizes,int u)
{
    if(u == n){
        int cnt = 0;
        res[*returnSize] = malloc(sizeof(int)*100010);
        for(int i = 0; i < n; i++){
            if(visit[i]){
                res[*returnSize][cnt++] = nums[i];
            }
        }
        int t = *returnSize;
        (*returnColumnSizes)[t] = cnt;  //这里这么写会缓冲区溢出，但是我没明白怎么就溢出了
        (*returnSize)++;
         return;
    }
    visit[u] = 1;
    dfs(returnSize,nums,n,returnColumnSizes,u+1);
    visit[u] = 0;
    dfs(returnSize,nums,n,returnColumnSizes,u+1);
    
}

int** subsets(int* nums, int numsSize, int* returnSize, int** returnColumnSizes){
    *returnColumnSizes = malloc(sizeof(int)*(1<<numsSize));
    visit = malloc(sizeof(int)*(numsSize+10));
    res = malloc(sizeof(int*)*(1000000));
    *returnSize = 0;
    dfs(returnSize,nums,numsSize,returnColumnSizes,0);
    return res;
}

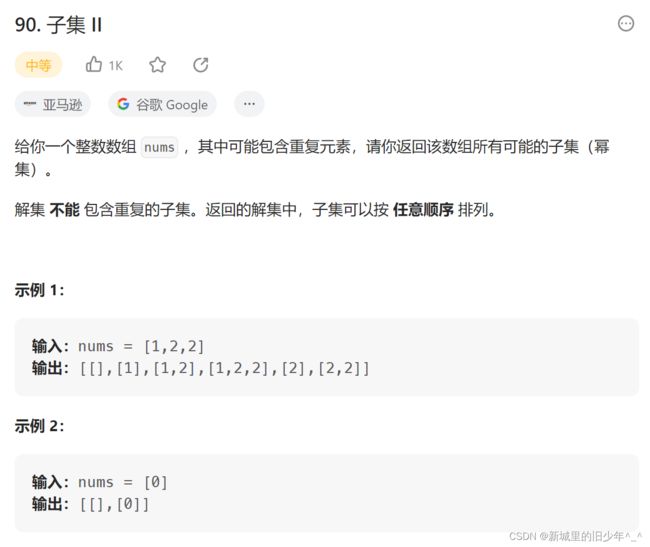
leetcode90 子集2（需要去重）

/**
 * Return an array of arrays of size *returnSize.
 * The sizes of the arrays are returned as *returnColumnSizes array.
 * Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().
 */
int *visit;
int *path;
int cnt;
int **res;
int cmp(const void *a,const void *b)
{
    return *(int*)a - *(int*)b;
}

void dfs(int **res,int* nums,int n,int *returnSize,int** returnColumnSizes,int u)
{
    if(u == n){
        res[*returnSize] = malloc(sizeof(int)*10000);
        int cnt = 0;
        for(int i = 0; i < n; i++){
            if(visit[i]){
                res[*returnSize][cnt++] = nums[i];
            }
        }
        (*returnColumnSizes)[*returnSize] = cnt;
        (*returnSize)++;
        return;
    }
    //去重时，不执行不选nums[i]的，然后看nums[i-1] == nums[i]且nums[i-1]是不是还没选过
    visit[u] = 0;
    path[cnt++] = nums[u];
    dfs(res,nums,n,returnSize,returnColumnSizes,u+1);
    if(u && nums[u-1] == nums[u] && !visit[u-1]) return;
    visit[u] = 1;
    cnt--;
    dfs(res,nums,n,returnSize,returnColumnSizes,u+1);
}

int** subsetsWithDup(int* nums, int numsSize, int* returnSize, int** returnColumnSizes){
    qsort(nums,numsSize,sizeof(int),cmp);
    *returnSize = 0;
    *returnColumnSizes = malloc(sizeof(int)*10000);
    visit = malloc(sizeof(int)*10000);
    path = malloc(sizeof(int)*10000);
    res = malloc(sizeof(int*)*10000);
    dfs(res,nums,numsSize,returnSize,returnColumnSizes,0);
    return res;
}

Leetcode77

/**
 * Return an array of arrays of size *returnSize.
 * The sizes of the arrays are returned as *returnColumnSizes array.
 * Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().
 */
int** res;
int visit[30];

void dfs(int n,int k,int u,int pos,int *returnSize,int** returnColumnSizes)
{
    if(n - pos + 1 + u < k) return;
    if(u == k){
        res[*returnSize] = malloc(sizeof(int)*30);
        int cnt = 0;
        for(int i = 1; i <= n; i++){
            if(visit[i]){
                res[*returnSize][cnt++] = i;
            }
        }
        (*returnColumnSizes)[*returnSize] = cnt; //必须写(*returnColumnSizes)[*returnSize] 带括号！！
        (*returnSize)++;
        return;
    }
    visit[pos] = 1;  //这里要先弄选这个数的方案，不能把visit[pos]=0放这里，要不会有问题
    dfs(n,k,u+1,pos+1,returnSize,returnColumnSizes);
    visit[pos] = 0;
    dfs(n,k,u,pos+1,returnSize,returnColumnSizes);
}

int** combine(int n, int k, int* returnSize, int** returnColumnSizes){
    memset(visit,0,sizeof(visit));
    res = malloc(sizeof(int)*300000000);
    *returnSize = 0;
    *returnColumnSizes = malloc(sizeof(int)*3000000);
    dfs(n,k,0,1,returnSize,returnColumnSizes);
    return res;
}

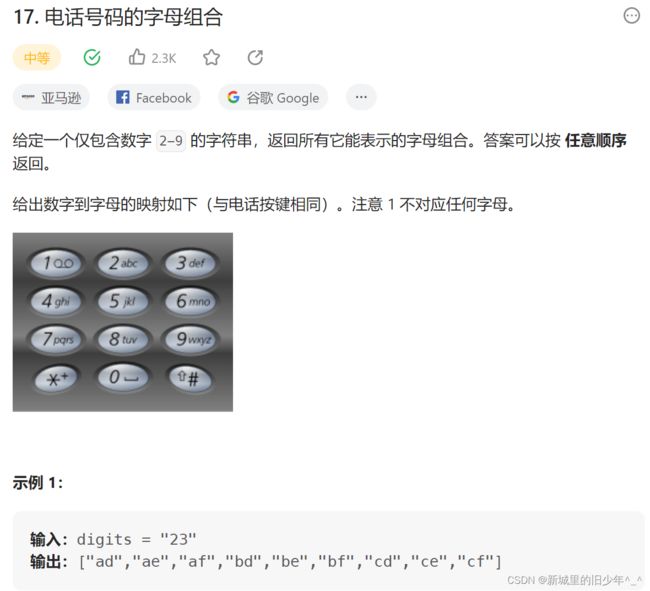
Leetcode17电话号码组合

char str[10][10] = {"\0","\0","abc\0","def\0","ghi\0","jkl\0","mno\0","pqrs\0","tuv\0","wxyz\0"};
char** res;
char path[100000];
int cnt = 0;

void dfs(char* digits,int* returnSize,int n,int u)
{
    if(u == n){
        printf("%d\n",cnt);
        res[*returnSize] = malloc(sizeof(char)*(n+10));
        for(int i = 0; i < cnt; i++){
            res[*returnSize][i] = path[i];
        }
        res[*returnSize][strlen(path)] = '\0';
        (*returnSize)++;
        return;
    }
    int num = digits[u] - '0'; 
    int len = strlen(str[num]);
    for(int i = 0; i < len; i++){
        path[cnt++] = str[digits[u] - '0'][i];
        dfs(digits,returnSize,n,u+1);
        cnt--; 
    }
    return;
}

char ** letterCombinations(char * digits, int* returnSize){
    if(!strlen(digits)){
        *returnSize = 0;
        return res;
    }
    *returnSize = 0;  //这个初始化必须有
    res = malloc(sizeof(char*)*1000000);
    memset(path,'\0',sizeof(path));
    dfs(digits,returnSize,strlen(digits),0);

    return res;
}

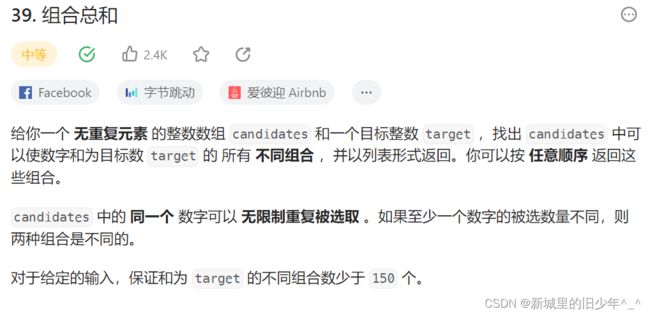
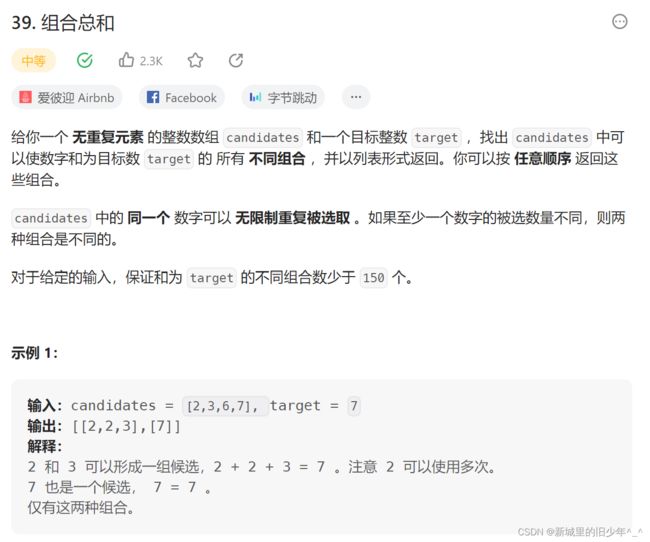
Leetcode39组合总和

/**
 * Return an array of arrays of size *returnSize.
 * The sizes of the arrays are returned as *returnColumnSizes array.
 * Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().
 */
int **res;
int* path;
int cnt = 0;
int visit[500];
void dfs(int* candidates,int n,int target,int* returnSize,int** returnColumnSizes,int sum,int pos)
{
    if(pos == n){//pos==n表示遍历完一遍这个数组，每个位置有选和不选
        if(sum == target){
            res[*returnSize] = malloc(sizeof(int)*500);
            for(int i = 0; i < cnt; i++){
                res[*returnSize][i] = path[i];
            }
            (*returnColumnSizes)[*returnSize] = cnt;
            (*returnSize)++;
        }
        return;
    } 
    for(int i = 0; candidates[pos] * i <= target;i++){ //i代表这个数被使用几次
        if(i){
            visit[candidates[pos]]++;
            path[cnt++] = candidates[pos];
            sum += candidates[pos];
        }
        dfs(candidates,n,target,returnSize,returnColumnSizes,sum,pos+1);
    }
    cnt -= visit[candidates[pos]];
    visit[candidates[pos]] = 0;
}

int** combinationSum(int* candidates, int candidatesSize, int target, int* returnSize, int** returnColumnSizes){
    if(candidatesSize == 0){
        *returnSize = 0;
        return res;
    }
    memset(visit,0,sizeof(visit));
    res = malloc(sizeof(int*)*500);
    path = malloc(sizeof(int)*500);
    (*returnColumnSizes) = malloc(sizeof(int)*500);
    *returnSize = 0;
    dfs(candidates,candidatesSize,target,returnSize,returnColumnSizes,0,0);
    return res;
}

组合总和二

int** res;
int* path;
int cnt;
int visit[110];
int cmp(const void* a,const void *b)
{
    return *(int*)a - *(int*)b;
}

void dfs(int* candidates,int n,int target,int *returnSize,int** returnColumnSizes,int sum,int pos)
{
    if(pos == n){
        if(sum == target){
            res[*returnSize] = malloc(sizeof(int)*1100);
            for(int i = 0; i <cnt; i++) res[*returnSize][i] = path[i];
            (*returnColumnSizes)[*returnSize] = cnt;
            (*returnSize)++;
        }
        return;
    }
    visit[pos] = 0;
    dfs(candidates,n,target,returnSize,returnColumnSizes,sum,pos+1);
    if(pos && candidates[pos-1]==candidates[pos] && !visit[pos-1]) return;
    visit[pos] = 1;
    path[cnt++] = candidates[pos];
    dfs(candidates,n,target,returnSize,returnColumnSizes,sum+candidates[pos],pos+1);
    cnt--;
    visit[pos] = 0;
    

}

int** combinationSum2(int* candidates, int candidatesSize, int target, int* returnSize, int** returnColumnSizes){
    qsort(candidates,candidatesSize,sizeof(int),cmp);
    res = malloc(sizeof(int*)*1100);
    path = malloc(sizeof(int)*1100);
    *returnColumnSizes = malloc(sizeof(int)*1100);
    memset(visit,0,sizeof(visit));
    *returnSize = 0;
    if(!candidatesSize) return res;
    dfs(candidates,candidatesSize,target,returnSize,returnColumnSizes,0,0);
    return res;
}

Leetcode397整数替换

int dfs(long long n)
{
    if(n==1) return 0;
    int res = 0x3f3f3f3f;
    if(n%2==0) res = fmin(res,dfs(n/2));
    if(n%2==1) res = fmin(res,fmin(dfs(n+1),dfs(n-1)));
    return res+1;
}

int integerReplacement(int n){
    int res = dfs(n);
    return res;
}

Leetcode 216

int* nums;
int** res;
int* path;
int cnt = 0;
int visit[10010];
void dfs(int* nums,int n,int k,int target,int pos,int sum,int* returnSize,int** returnColumnSizes)
{
    if(pos == n){
        if(sum == target && cnt == k){
            res[*returnSize] = malloc(sizeof(int)*10010);
            for(int i = 0; i < cnt; i++) res[*returnSize][i] = path[i];
            (*returnColumnSizes)[*returnSize] = cnt;
            (*returnSize)++;
        }
        return;
    }
    visit[pos] = 1;
    path[cnt++] = nums[pos];
    dfs(nums,n,k,target,pos+1,sum+nums[pos],returnSize,returnColumnSizes);
    visit[pos] = 0;
    cnt--;
    dfs(nums,n,k,target,pos+1,sum,returnSize,returnColumnSizes);
}

int** combinationSum3(int k, int n, int* returnSize, int** returnColumnSizes){
    res = malloc(sizeof(int*)*10010);
    path = malloc(sizeof(int)*10010);
    memset(visit,0,sizeof(visit));
    nums = malloc(sizeof(int)*10010);
    *returnColumnSizes = malloc(sizeof(int)*10010);
    for(int i = 0; i < 9; i++) nums[i] = i + 1;
    int len = 9;
    *returnSize = 0;
    dfs(nums,len,k,n,0,0,returnSize,returnColumnSizes);
    return res;
}

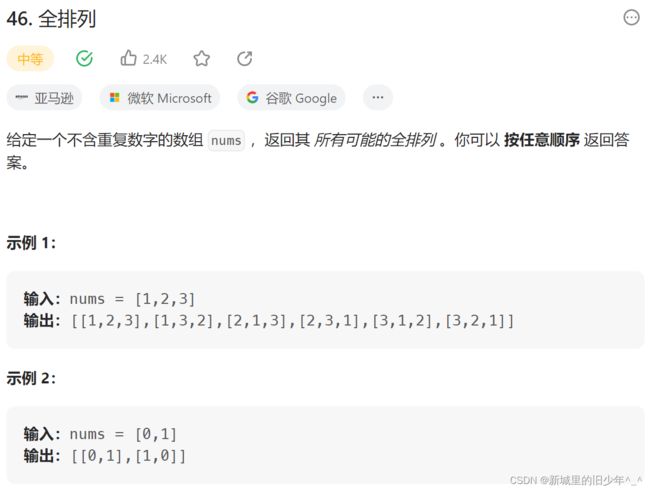
46全排列

int **res;
int* path;
int cnt = 0;
int visit[2000];

void dfs(int* nums,int n, int* returnSize,int** returnColumnSizes,int u)
{
    if(u == n){
        res[*returnSize] = malloc(sizeof(int)*2000);
        for(int i = 0; i < cnt; i++) res[*returnSize][i] = path[i];
        (*returnColumnSizes)[*returnSize] = cnt;
        (*returnSize)++;
        return;
    }
    for(int i = 0; i < n; i++){
        if(!visit[i]){
            visit[i] = 1;
            path[cnt++] = nums[i];
            dfs(nums,n,returnSize,returnColumnSizes,u+1);
            cnt--;
            visit[i] = 0;
        }
    }
}

int** permute(int* nums, int numsSize, int* returnSize, int** returnColumnSizes){
    res = malloc(sizeof(int*)*2000);
    path = malloc(sizeof(int)*2000);
    memset(visit,0,sizeof(visit));
    *returnSize = 0;
    if(!numsSize) return res;
    *returnColumnSizes = malloc(sizeof(int)*2000);
    dfs(nums,numsSize,returnSize,returnColumnSizes,0);
    return res;
}

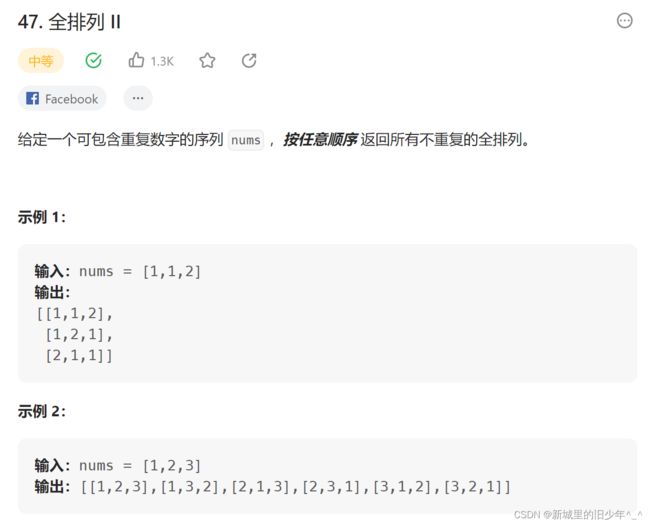
Leetcode47

int** res;
int* path;
int cnt = 0;
int  visit[2000];
int cmp(const void* a,const void* b)
{
    return *(int*)a - *(int*)b;
}

void dfs(int* nums,int n,int *returnSize,int** returnColumnSizes,int u)
{
    if(u == n){
        res[*returnSize] = malloc(sizeof(int)*2000);
        for(int i = 0; i < cnt; i++) res[*returnSize][i] = path[i];
        (*returnColumnSizes)[*returnSize] = cnt;
        (*returnSize)++;
        return;
    }
    for(int i = 0; i < n; i++){
        if(visit[i]) continue;
        if(i && nums[i] == nums[i-1] && !visit[i-1]) continue;
        visit[i] = 1;
        path[cnt++] = nums[i];
        dfs(nums,n,returnSize,returnColumnSizes,u+1);
        cnt--;
        visit[i] = 0;
    }
}

int** permuteUnique(int* nums, int numsSize, int* returnSize, int** returnColumnSizes){
    qsort(nums,numsSize,sizeof(int),cmp);
    res = malloc(sizeof(int*)*2000);
    path = malloc(sizeof(int)*2000);
    memset(visit,0,sizeof(visit));
    *returnSize = 0;
    if(!numsSize) return res;
    (*returnColumnSizes) = malloc(sizeof(int)*2000);
    dfs(nums,numsSize,returnSize,returnColumnSizes,0);
    return res;
}

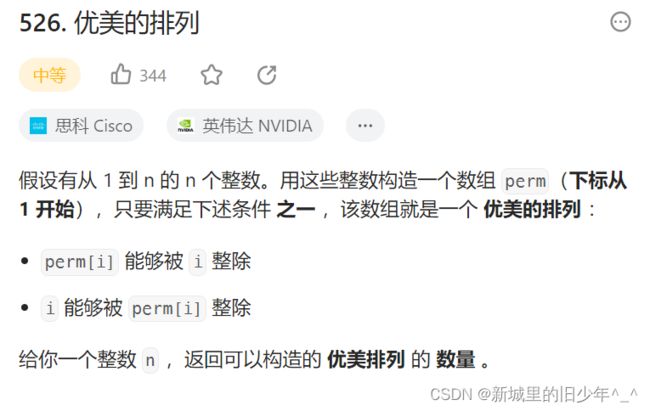
Leetcode526优美的排列

这个题用全排列来做，然后中途可以有剪枝

bool visit[20];
int res;
int n;
void dfs(int u)
{
    if(u == (n+1)){
        res++;
        return;
    }
    for(int i = 1; i <= n; i++){
        if(!visit[i]){
            if(i%u == 0 || u%i==0){
                visit[i] = true;
                dfs(u+1);
                visit[i] = false;
            }
        }
    }
}

int countArrangement(int _n){
    res = 0;
    n = _n;
    memset(visit,0,sizeof(visit));
    for(int i = 1; i <= n; i++){
        visit[i] = true;
        dfs(2);
        visit[i] = false;
    }
    return res;
}

Leetcode131

Leetcode93

Leetcode64

static int res;
int dx[2] = {1,0},dy[2] = {0,1};
int max(int a,int b)
{
    return a>b?a:b;
}
int min(int a,int b)
{
    return a<b?a:b;
}
void dfs(int** grid,int n,int m,int x,int y,int path)
{
    if(x >= n || y >= m) return;
    if(x == n - 1 && y == m - 1){
        res = min(res,path+grid[x][y]);
        return;
    }
    path += grid[x][y];
    for(int i = 0; i < 2; i++){
        int nx = x + dx[i],ny = y + dy[i];
        dfs(grid,n,m,nx,ny,path);
    }

}

int minPathSum(int** grid, int gridSize, int* gridColSize){
    res = 1000000;
    int n = gridSize, m = gridColSize[0];
    dfs(grid,n,m,0,0,0);
    return res;
}

Leetcode124二叉树中的最大路径和

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
static int res;
int dfs(struct TreeNode* root)  //返回以这个点开始到所有其子孙叶子节点中，最长的路径
{
    if(root == NULL){
        return 0;
    }
    int ans = root -> val;
    int left = fmax(dfs(root->left),0);
    int right = fmax(dfs(root->right),0);
    res = fmax(res,ans+left+right); //寻找  /\ 这样的路径
    return ans + fmax(left,right);
}

int maxPathSum(struct TreeNode* root){
    res = -1100;
    dfs(root);
    return res;
}

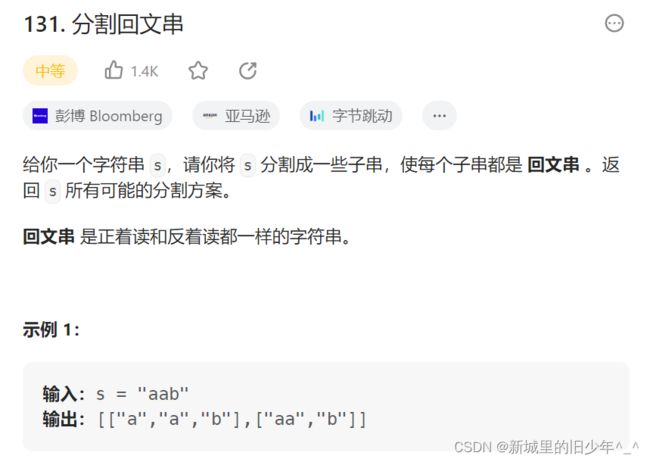
Leetcode131分割回文串

/**
 * Return an array of arrays of size *returnSize.
 * The sizes of the arrays are returned as *returnColumnSizes array.
 * Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().
 */

bool ifstr(char * s, int i, int j)//判断是否为回文串
{
    while(i <= j)
    {
        if(s[i] != s[j])
            return false;
        i++;
        j--;
    }
    return true;
}


void dfs(char * s, char *** ans, int * returnSize, int ** returnColumnSizes, int len, char ** path, int path_i,int index)//递归回溯枚举子串
{
   
    if(index >= len)//切割到最后了，保存有效组合
    {
        ans[(*returnSize)] = (char**)malloc(sizeof(char *) * path_i);
        for(int i = 0; i < path_i; i++)
        {
            ans[(*returnSize)][i] = (char *)malloc(sizeof(char) * (len+1));
            strcpy(ans[(*returnSize)][i], path[i]);
        }
        (*returnColumnSizes)[(*returnSize)++] = path_i;
        return;
    }
    for(int i = index; i < len; i++)
    {
        if(ifstr(s, index, i) == false) continue;//剪枝，当前不满足切割条件，就没必要在枚举了
        strncpy(path[path_i], s+index, i-index+1);//满足切割条件，保存子串
        path[path_i][i-index+1] = '\0';
        dfs(s, ans, returnSize, returnColumnSizes, len, path, path_i+1, i+1);//递归重复之前动作
        //其中path_i+1, i+1 都是回溯，因为是实参传个形参，形参不会改变实参的值，所以实际没有变，相等于 i++，再i--
    }
    return;
}

char *** partition(char * s, int* returnSize, int** returnColumnSizes){
    char *** ans = (char ***)malloc(sizeof(int **) * 50000);
    (*returnColumnSizes) = (int *)malloc(sizeof(int) * 50000);
    int len = strlen(s);
    char ** path = (char **)malloc(sizeof(char *) * len);
    for(int i = 0; i < len; i++)
    {
        path[i] = (char *)malloc(sizeof(char) * (len+1));
    }
    *returnSize = 0;//初始化变量
    dfs(s, ans, returnSize, returnColumnSizes,len, path, 0, 0);
    return ans;
}

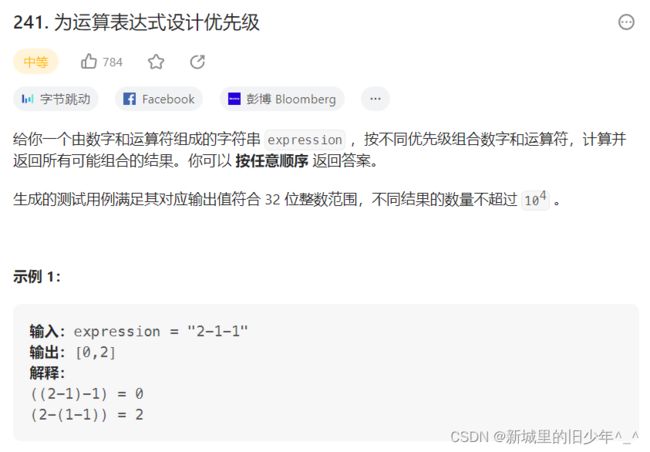
Leetcode241

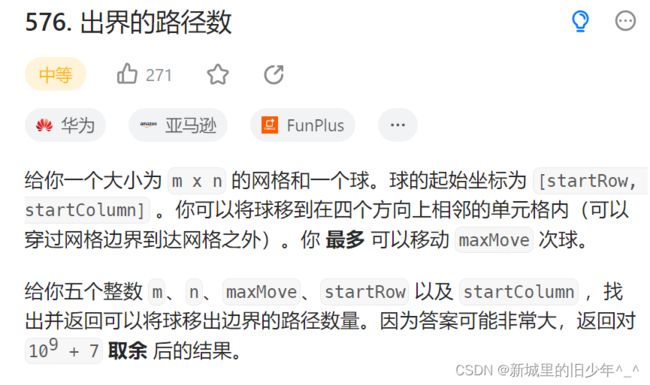
Leetcode576出界路径数

题目详解

方法一:剪枝DFS

static int res;
int dx[4] = {0,0,1,-1},dy[4] = {1,-1,0,0};
void dfs(int m,int n,int u,int v,int k)
{
    if(u < 0 || u >= m || v < 0 || v >= n){
        res++;
        return;
    }
    if(k == 0) return;
    //剪枝:如果小球怎样都不能移出,直接退出
    if(u-k>=0 && v-k>=0 && u+k<m && v+k<n) return;
    for(int i = 0; i < 4; i++){
        int nx = u + dx[i], ny = v + dy[i];
        dfs(m,n,nx,ny,k-1);
    }
}

int findPaths(int m, int n, int maxMove, int startRow, int startColumn){
    res = 0;
    dfs(m,n,startRow,startColumn,maxMove);
    return res;
}

AC:记忆化搜索DFS

#define mod (long long)(1e9+7)
int dx[4] = {0,0,1,-1},dy[4] = {1,-1,0,0};
int f[60][60][60]; //f[i][j][k]表示从(i,j)这个点移动k次,最终出界的路径数

int dfs(int m,int n,int u,int v,int k)
{
    if(u < 0 || u >= m || v < 0 || v >= n){
        return 1;
    }
    if(k == 0) return 0;
    //剪枝:如果小球怎样都不能移出,直接退出
    if(u-k>=0 && v-k>=0 && u+k<m && v+k<n) return 0;
    //剪枝:如果这个点之前得到了走k步出界的结果,直接返回之前的结果,不在搜索了
    if(f[u][v][k] != -1) return f[u][v][k];
    int ans = 0;
    for(int i = 0; i < 4; i++){
        int nx = u + dx[i], ny = v + dy[i];
        ans = (ans + dfs(m,n,nx,ny,k-1))%mod;  //这种取余的一定是写成a = (a+c)%mod 一定不是 a += c%mod
    }
    f[u][v][k] = ans;
    return ans;
}

int findPaths(int m, int n, int maxMove, int startRow, int startColumn){
    memset(f,0,sizeof(f));
    for(int i  = 0; i < m; i++){
        for(int j = 0; j <n; j++){
            for(int k = 0; k <= maxMove; k++) f[i][j][k] = -1; //-1表示(i,j)这个点移动k次出界的情况还没被访问过
        }
    }
    int res  =  dfs(m,n,startRow,startColumn,maxMove);
    return res;
}

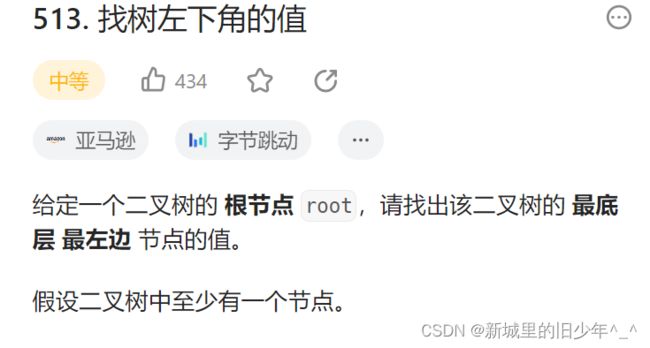
Leetcode513找到树左下角值

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
static int res;
static int max_level;
void dfs(struct TreeNode* root,int u){
    if(!root) return;
    if(!root->left && !root->right && u > max_level){
        max_level = u;
        res = root->val;
        return;
    }
    dfs(root->left,u+1);
    dfs(root->right,u+1);
}

int findBottomLeftValue(struct TreeNode* root){
    res = 0,max_level = -1;
    dfs(root,0);
    return res;
}

Leetcode22括号生成

char* path;
int cnt;
void dfs(char** res,int* returnSize,int n,int left,int right)
{
    if(left == n && right == n){
        res[*returnSize] = malloc(sizeof(char)*5000);
        for(int i = 0; i < cnt; i++) res[*returnSize][i] = path[i];
        res[*returnSize][cnt] = '\0';
        (*returnSize)++;
        return;
    }
    if(left < n){
        path[cnt++] = '(';
        dfs(res,returnSize,n,left+1,right);
        cnt--;
    }
    if(right < left){
        path[cnt++] = ')';
        dfs(res,returnSize,n,left,right+1);
        cnt--;
    }
}

char ** generateParenthesis(int n, int* returnSize){
    char** res = malloc(sizeof(char*)*5000);
    path = malloc(sizeof(char)*5000);
    cnt = 0;
    *returnSize = 0;
    dfs(res,returnSize,n,0,0);
    return res;
}

Leetcode894所有可能的真二叉树

Leetcode95不同的二叉搜索树II

此题是要输出所有可能的方案，所以用DFS暴搜一下，如果只要求方案数，那么用DP即可

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */


/**
 * 给每个节点一个编号从1~n
 */
struct TreeNode** dfs(int l,int r,int* returnSize)
{
    if(l > r){
        //空树的集合
        struct TreeNode** res = malloc(sizeof(struct TreeNode*));
        *returnSize = 1;
        res[0] = NULL;
        return res;
    }
    struct TreeNode** res = malloc(sizeof(struct TreeNode*)*10000);
    for(int i = l; i <= r; i++){
        int* leftsize = malloc(sizeof(int));
        int* rightsize = malloc(sizeof(int));
        *leftsize = 0,*rightsize = 0;
        struct TreeNode** left = dfs(l,i-1,leftsize);
        struct TreeNode** right = dfs(i+1,r,rightsize);
        for(int j = 0; j < *leftsize; j++){
            for(int k = 0; k < *rightsize; k++){
                struct TreeNode* root = malloc(sizeof(struct TreeNode));
                root->val = i;
                root->left = left[j];
                root->right = right[k];
                res[*returnSize] = root;
                (*returnSize)++;
            }
        }
    }
    return res;
}

struct TreeNode** generateTrees(int n, int* returnSize){
    *returnSize = 0;
    return dfs(1,n,returnSize);
}

Leetcode98验证二叉搜索树

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
 //输出中序遍历，然后和排序后的数组比较即可
long long* res;
long long* ans;
int cmp(const void* a,const void *b)
{
    long long* aa = (long long*)a;  //用long long等别写*(long long*)a - *(long long*)b因为cmp是个int，这样可能溢出
    long long* bb = (long long*)b;
    if(*aa > *bb) return 1;
    return -1;
}
void dfs(struct TreeNode* root,int* size)
{
    if(!root) return;
    dfs(root->left,size);
    res[*size] = root->val;
    (*size)++;
    dfs(root->right,size);

}

bool isValidBST(struct TreeNode* root){
    int size = 0;
    res = malloc(sizeof(long long)*10000);
    ans = malloc(sizeof(long long)*10000);
    dfs(root,&size);
    for(int i = 0; i < size; i++) ans[i] = res[i];
    qsort(ans,size,sizeof(ans[0]),cmp);
    bool flag = true;
    for(int i = 0; i < size; i++){
        if(i > 0 && ans[i] == ans[i-1]){
            flag = false;
            break;
        }
        if(res[i] != ans[i]){
            flag = false;
            break;
        }
    }
    for(int i = 0; i < size; i++) printf("%lld ",ans[i]);
    printf("\n");
    for(int i = 0; i < size; i++) printf("%lld ",res[i]);
    return flag;
}

Leetcode99恢复二叉搜索树

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
long long* res;
long long* ans;
int num[10];
int cmp(const void* a,const void* b)
{
    long long *aa = (long long*)a;
    long long *bb = (long long*)b;
    if(*aa > *bb) return 1;
    return -1;
}

void dfs(struct TreeNode* root,int* n)
{
    if(!root) return;
    dfs(root->left,n);
    res[*n] = root->val;
    (*n)++;
    dfs(root->right,n);
}

void dfs2(struct TreeNode* root)
{
    if(!root) return;
    if(root->val == num[0]) root->val = num[1];
    else if(root->val == num[1]) root->val = num[0];
    dfs2(root->left);
    dfs2(root->right);
}

void recoverTree(struct TreeNode* root){
    res = malloc(sizeof(long long)*1010);
    ans = malloc(sizeof(long long)*1010);
    memset(num,0,sizeof(num));
    int n = 0;
    dfs(root,&n);
    
    for(int i = 0; i < n; i++){
        ans[i] = res[i];
    }
    qsort(ans,n,sizeof(ans[0]),cmp);
    for(int i = 0; i < n; i++){
        if(ans[i] != res[i]){
            num[0] = ans[i];
            num[1] = res[i];
            break;
        }
    }
    dfs2(root);
}

Leetcode102层序遍历

这个题是要返回每一层的节点，然后用一个队列，每次找到这一层的所有节点

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */


/**
 * Return an array of arrays of size *returnSize.
 * The sizes of the arrays are returned as *returnColumnSizes array.
 * Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().
 */
int** levelOrder(struct TreeNode* root, int* returnSize, int** returnColumnSizes){
    int** res = malloc(sizeof(int*)*1000);
    *returnColumnSizes = malloc(sizeof(int)*1000);
    *returnSize = 0;
    if(!root) return res;
    struct TreeNode* queue[10100];  
    int front = 0,tail = -1;
    queue[++tail] = root;
    while(front<=tail){
        int start = front,end = tail;
        res[*returnSize] = malloc(sizeof(int)*10100);
        (*returnColumnSizes)[*returnSize] = end - start + 1;
        for(int i = 0; i <= end - start; i++){
            res[*returnSize][i] = queue[i+start]->val;
            if(queue[i+start]->left != NULL) queue[++tail] = queue[start+i]->left;
            if(queue[i+start]->right) queue[++tail] = queue[start+i]->right;
        }
        (*returnSize)++;
        front = end + 1;
    }
    return res;
}

Leetcode103二叉树锯齿形遍历

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */


/**
 * Return an array of arrays of size *returnSize.
 * The sizes of the arrays are returned as *returnColumnSizes array.
 * Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().
 */
int** zigzagLevelOrder(struct TreeNode* root, int* returnSize, int** returnColumnSizes){
    int** res = malloc(sizeof(int*)*1010);
    (*returnColumnSizes) = malloc(sizeof(int)*1010);
    *returnSize = 0;
    if(!root) return res;
    struct TreeNode* queue[1010];
    int ff = 0,tt = -1, level = 0; //偶数层正序输出，奇数层，倒序输出
    queue[++tt] = root;
    while(ff <= tt)
    {
        int start = ff, end = tt;
        res[*returnSize] = malloc(sizeof(int)*1010);
        (*returnColumnSizes)[*returnSize] = end - start + 1;
        for(int i = start; i <= end; i++){
            if(queue[i]->left) queue[++tt] = queue[i]->left;
            if(queue[i]->right) queue[++tt] = queue[i]->right;
        }
        if(level%2 == 0){
            for(int i = 0; i < end - start + 1; i++){
                res[*returnSize][i] = queue[start + i]->val;
            }
        }
        else if(level%2){
            for(int i = 0; i <= end - start; i++){
                res[*returnSize][i] = queue[end-i]->val;
            }
        }
        (*returnSize)++;
        level++;
        ff = end + 1;
    }
    return res;
}

Leetcode107二叉树层序遍历II

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */


/**
 * Return an array of arrays of size *returnSize.
 * The sizes of the arrays are returned as *returnColumnSizes array.
 * Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().
 */
int** levelOrderBottom(struct TreeNode* root, int* returnSize, int** returnColumnSizes){
    int** res = malloc(sizeof(int*)*1010);
    *returnSize = 0;
    (*returnColumnSizes) = malloc(sizeof(int)*1010);
    if(!root) return res;
    struct TreeNode* queue[10100];
    int front = 0, tail = -1;
    queue[++tail] = root;
    while(front <= tail){
        int start = front, end = tail;
        res[*returnSize] = malloc(sizeof(int)*1010);
        (*returnColumnSizes)[*returnSize] = end - start + 1;
        for(int i = 0; i <= end-start; i++){
            res[*returnSize][i] = queue[start+i]->val;
            if(queue[start+i]->left) queue[++tail] = queue[start+i]->left;
            if(queue[start+i]->right) queue[++tail] = queue[start+i]->right;
        }
        (*returnSize)++;
        front = end + 1;
    }
    int tmp[10100];
    memset(tmp,0,sizeof(tmp));
    int n = *returnSize;
    for(int i = 0; i < n; i++) tmp[i] = (*returnColumnSizes)[i];
    int l = 0, r = n-1;
    while(l < r)
    {
        int t = (*returnColumnSizes)[l];
        (*returnColumnSizes)[l] = (*returnColumnSizes)[r];
        (*returnColumnSizes)[r] = t;
        l++,r--;
    }
    int** ans = malloc(sizeof(int*)*1010);
    for(int i = 0; i < n; i++){
        ans[i] = malloc(sizeof(int)*1010);
        for(int j = 0; j < tmp[n-1-i]; j++){
            ans[i][j] = res[n-1-i][j];
        }
    }
    return ans;

}

Leetcode105前序遍历+中序遍历构造二叉树

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
int hash[10010];
struct TreeNode* build(int* preorder,int prel,int prer,int* inorder,int inl,int inr)
{
    if(prel > prer){
        return NULL;
    }
    struct TreeNode* root = malloc(sizeof(struct TreeNode));
    root->val = preorder[prel];
    int k = hash[root->val+3010] - inl;
    root->left = build(preorder,prel+1,k+prel,inorder,inl,inl+k-1);
    root->right = build(preorder,prer-(inr-inl-k-1),prer,inorder,inl+k+1,inr);
   return root;
}

struct TreeNode* buildTree(int* preorder, int preorderSize, int* inorder, int inorderSize){
    if(!preorderSize) return NULL;
    memset(hash,0,sizeof(hash));
    struct TreeNode* root = malloc(sizeof(struct TreeNode));
    for(int i = 0; i < inorderSize; i++) hash[inorder[i]+3010] = i; //记录这个数在中序遍历中的位置，便于查找
    root->val = preorder[0];
    int k = hash[preorder[0]+3010];
    root->left = build(preorder,1,k,inorder,0,k-1);
    root->right = build(preorder,k+1,preorderSize-1,inorder,k+1,inorderSize-1);
    return root;
}

Leetcode106从中序遍历和后序遍历构造二叉树

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
int hash[6020];
struct TreeNode* build(int* inorder,int inl,int inr,int* postorder,int postl,int postr)
{
    if(inl > inr) return NULL;
    struct TreeNode* root = malloc(sizeof(struct TreeNode));
    root->val = postorder[postr];
    int k = hash[root->val+3000] - inl;
    root->left = build(inorder,inl,inl+k-1,postorder,postl,postl+k-1);
    root->right = build(inorder,inl+k+1,inr,postorder,postl+k,postr-1);
    return root;
}

struct TreeNode* buildTree(int* inorder, int inorderSize, int* postorder, int postorderSize){
    memset(hash,0,sizeof(hash));
    int n = inorderSize;
    for(int i = 0; i < n; i++) hash[inorder[i]+3000] = i;
    struct TreeNode* root = build(inorder,0,n-1,postorder,0,n-1);
    return root;
}

Leetcode108有序数组转化为平衡BST

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
struct TreeNode* build(int* nums,int l,int r)
{
    if(l > r) return NULL;
    struct TreeNode* root = malloc(sizeof(struct TreeNode));
    int mid = (l+r)/2;
    root->val = nums[mid];
    root->left = build(nums,l,mid-1);
    root->right = build(nums,mid+1,r);
    return root; 
}

struct TreeNode* sortedArrayToBST(int* nums, int numsSize){
    return build(nums,0,numsSize-1);
}

Leetcode110平衡二叉树

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
int find_height(struct TreeNode* root)
{
    if(!root) return 0;
    int left = find_height(root->left);
    int right = find_height(root->right);
    return fmax(left,right) + 1;
}

bool dfs(struct TreeNode* root)
{
    if(!root) return true;
    int left = find_height(root->left);
    int right = find_height(root->right);
    if(abs(left-right) >= 2) return false;
    return dfs(root->left) && dfs(root->right);
}

bool isBalanced(struct TreeNode* root){
    return dfs(root);
}

Leetcode112路径总和

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
bool dfs(struct TreeNode* root,int target,int sum)
{
    if(root->left == NULL && root->right == NULL){
        if((sum+root->val)==target) return true;
        return false;
    }
    bool left = false, right = false;
    if(root->left) left = dfs(root->left,target,sum+root->val);
    if(root->right) right = dfs(root->right,target,sum+root->val);
    return left || right;
}

bool hasPathSum(struct TreeNode* root, int targetSum){
    if(!root) return false;
    return dfs(root,targetSum,0);
}

Leetcode113路径总和II

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
int** res;
int* path;
void dfs(struct TreeNode* root, int target, int sum,int* returnSize,int** returnColumnSizes,int cnt)
{
    if(!root->left && !root->right)
    {
        if(target == (sum+root->val))
        {
            res[*returnSize] = malloc(sizeof(int)*1010);
            path[cnt++] = root->val;
            for(int i = 0; i <cnt; i++) res[*returnSize][i] = path[i];
            (*returnColumnSizes)[*returnSize] = cnt;
            (*returnSize)++;
        }
        return;
    }
    path[cnt++] = root->val;
    if(root->left) dfs(root->left,target,sum+root->val,returnSize,returnColumnSizes,cnt);
    if(root->right) dfs(root->right,target,sum+root->val,returnSize,returnColumnSizes,cnt);
}

int** pathSum(struct TreeNode* root, int target, int* returnSize, int** returnColumnSizes){
    res = malloc(sizeof(int*)*1010);
    path = malloc(sizeof(int)*1010);
    int cnt = 0;
    (*returnColumnSizes) = malloc(sizeof(int)*1010);
    *returnSize = 0;
    if(!root) return res;
    dfs(root,target,0,returnSize,returnColumnSizes,cnt);
    return res;
}

Leetcode337打家劫舍III

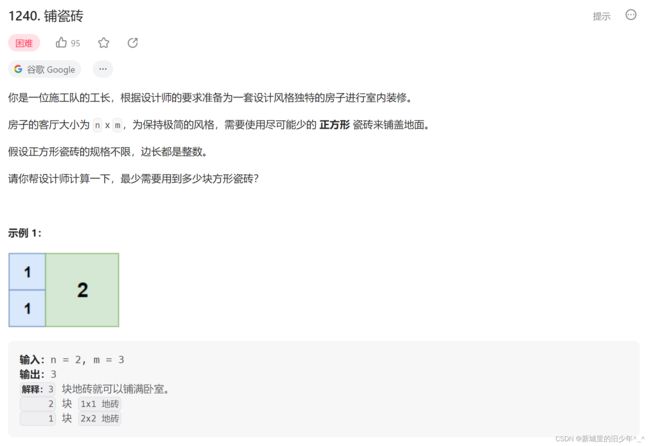
Leetcode 1240铺瓷砖

bool visit[200][200];
int res;
bool check(int x,int y,int len)
{
    for(int i = x; i < x + len; i++){
        for(int j = y; j < y + len; j++){
            if(visit[i][j]) return false;
        }
    }
    return true;
}

void fill(int x,int y, int len,bool flag)
{
    for(int i = x; i < x + len; i++){
        for(int j = y; j < y + len; j++){
            visit[i][j] = flag;
        }
    }
}

void dfs(int n,int m,int x,int y,int cnt) //cnt表示铺到(x，y)这个点之前已经铺了多少个正方形了
{
    if(cnt >= res) return; //如果已经比铺满用的正方形块更多，那么直接退出即可
    if(y == m){
        x = x + 1;
        y = 0;
    }
    if(x == n){
        res = cnt;
    }
    else{
        if(visit[x][y]) dfs(n,m,x,y+1,cnt);
        else{
            for (int len = fmin(n - x, m - y); len; len -- ) {
                    if (check(x, y, len)) {
                        fill(x, y, len, true);
                        dfs(n,m, x, y + 1, cnt + 1);
                        fill(x, y, len, false);
                    }
                }
        }
    }
}


int tilingRectangle(int n, int m){
    //先行后列，枚举每个(i，j)作为正方形的左上角，然后枚举长度len
    memset(visit,0,sizeof(visit));
    res = 410; //res 全局变量，表示铺满整个正方形需要的最小的正方形块数目
    dfs(n,m,0,0,0);
    return res;
}

Leetcode967

/**
 *  暴搜一下，枚举每个位置即可
 */
int* res;
void dfs(int n, int k, int u,int path, int *returnSize)
{
    if(u == n){
        res[*returnSize] = path;
        (*returnSize)++;
        return;
    }
    if(path%10-k >= 0) dfs(n,k,u+1,path*10+path%10-k,returnSize);
    if(k==0) return;
    if(path%10+k <= 9) dfs(n,k,u+1,path*10+path%10+k,returnSize);
}


int* numsSameConsecDiff(int n, int k, int* returnSize){
    res = malloc(sizeof(int)*10010);
    *returnSize = 0;
    for(int i = 1; i <= 9; i++){
        dfs(n,k,1,i,returnSize);
    }
    return res;
}

你可能感兴趣的:(算法,深度优先,leetcode,宽度优先)

机器学习与深度学习间关系与区别 ℒℴѵℯ心·动ꦿ໊ོ꫞ 人工智能学习深度学习 python
一、机器学习概述定义机器学习（MachineLearning,ML）是一种通过数据驱动的方法，利用统计学和计算算法来训练模型，使计算机能够从数据中学习并自动进行预测或决策。机器学习通过分析大量数据样本，识别其中的模式和规律，从而对新的数据进行判断。其核心在于通过训练过程，让模型不断优化和提升其预测准确性。主要类型1.监督学习（SupervisedLearning）监督学习是指在训练数据集中包含输入
《投行人生》读书笔记小蘑菇的树洞
《投行人生》----作者詹姆斯-A-朗德摩根斯坦利副主席40年的职业洞见-很短小精悍的篇幅，比较适合初入职场的新人。第一部分成功的职业生涯需要规划1.情商归为适应能力分享与协作同理心适应能力，更多的是自我意识，你有能力识别自己的情并分辨这些情绪如何影响你的思想和行为。2.对于初入职场的人的建议，细节，截止日期和数据很重要截止日期，一种有效的方法是请老板为你所有的任务进行优先级排序。和老板喝咖啡的好
回溯 Leetcode 332 重新安排行程 mmaerd Leetcode刷题学习记录 leetcode 算法职场和发展
重新安排行程Leetcode332学习记录自代码随想录给你一份航线列表tickets，其中tickets[i]=[fromi,toi]表示飞机出发和降落的机场地点。请你对该行程进行重新规划排序。所有这些机票都属于一个从JFK（肯尼迪国际机场）出发的先生，所以该行程必须从JFK开始。如果存在多种有效的行程，请你按字典排序返回最小的行程组合。例如，行程[“JFK”,“LGA”]与[“JFK”,“LGB
Goolge earth studio 进阶4——路径修改与平滑陟彼高冈yu Google earth studio 进阶教程旅游
如果我们希望在大约中途时获得更多的城市鸟瞰视角。可以将相机拖动到这里并创建一个新的关键帧。camera_target_clip_7EarthStudio会自动平滑我们的路径，所以当我们通过这个关键帧时，不是一个生硬的角度，而是一个平滑的曲线。camera_target_clip_8路径上有贝塞尔控制手柄，允许我们调整路径的形状。右键单击，我们可以选择“平滑路径”，这是默认的自动平滑算法，或者我们可
基于社交网络算法优化的二维最大熵图像分割智能算法研学社（Jack旭）智能优化算法应用图像分割算法 php 开发语言
智能优化算法应用：基于社交网络优化的二维最大熵图像阈值分割-附代码文章目录智能优化算法应用：基于社交网络优化的二维最大熵图像阈值分割-附代码1.前言2.二维最大熵阈值分割原理3.基于社交网络优化的多阈值分割4.算法结果：5.参考文献：6.Matlab代码摘要：本文介绍基于最大熵的图像分割，并且应用社交网络算法进行阈值寻优。1.前言阅读此文章前，请阅读《图像分割：直方图区域划分及信息统计介绍》htt
509. 斐波那契数(每日一题) lzyprime
lzyprime博客(github)创建时间：2021.01.04qq及邮箱：2383518170leetcode笔记题目描述斐波那契数，通常用F(n)表示，形成的序列称为斐波那契数列。该数列由0和1开始，后面的每一项数字都是前面两项数字的和。也就是：F(0)=0，F(1)=1F(n)=F(n-1)+F(n-2)，其中n>1给你n，请计算F(n)。示例1：输入：2输出：1解释：F(2)=F(1)+
读书||陶新华《教育中的积极心理学》1—28 流水淙淙2022
读一本好书，尤如和一位高尚者对话，亦能对人的精神进行洗礼。但是若不能和实践结合起来，也只能落到空读书的状态。读书摘要与感想1、塞利格曼在《持续的幸福》一书中提出了幸福2.0理论，提出幸福由5个元素决定——积极情绪、投入的工作和生活、目标和意义、和谐的人际关系、成就感。2、人的大脑皮层在进行智力活动时，都伴有皮下中枢活动，对这些活动进行体验请假，并由此产生了情感解读。人的情绪情感体验总是优先于大脑的
121. 买卖股票的最佳时机薄荷糖的味道_fb40
给定一个数组，它的第i个元素是一支给定股票第i天的价格。如果你最多只允许完成一笔交易（即买入和卖出一支股票），设计一个算法来计算你所能获取的最大利润。注意你不能在买入股票前卖出股票。示例1:输入:[7,1,5,3,6,4]输出:5解释:在第2天（股票价格=1）的时候买入，在第5天（股票价格=6）的时候卖出，最大利润=6-1=5。注意利润不能是7-1=6,因为卖出价格需要大于买入价格。示例2:输入:
每日算法&面试题，大厂特训二十八天——第二十天（树）肥学 ⚡算法题⚡面试题每日精进 java 算法数据结构
目录标题导读算法特训二十八天面试题点击直接资料领取导读肥友们为了更好的去帮助新同学适应算法和面试题，最近我们开始进行专项突击一步一步来。上一期我们完成了动态规划二十一天现在我们进行下一项对各类算法进行二十八天的一个小总结。还在等什么快来一起肥学进行二十八天挑战吧！！特别介绍小白练手专栏，适合刚入手的新人欢迎订阅编程小白进阶python有趣练手项目里面包括了像《机器人尬聊》《恶搞程序》这样的有趣文章
回溯算法-重新安排行程 chirou_ 算法数据结构图论 c++图搜索
leetcode332.重新安排行程这题我还没自己ac过，只能现在凭着刚学完的热乎劲把我对题解的理解记下来。本题我认为对数据结构的考察比较多，用什么数据结构去存数据，去读取数据，都是很重要的。classSolution{private:unordered_map>targets;boolbacktracking(intticketNum,vector&result){//1.确定参数和返回值//2
C++ | Leetcode C++题解之第409题最长回文串 Ddddddd_158 经验分享 C++Leetcode 题解
题目：题解：classSolution{public:intlongestPalindrome(strings){unordered_mapcount;intans=0;for(charc:s)++count[c];for(autop:count){intv=p.second;ans+=v/2*2;if(v%2==1andans%2==0)++ans;}returnans;}};
Faiss：高效相似性搜索与聚类的利器网络·魚大数据 faiss
Faiss是一个针对大规模向量集合的相似性搜索库，由FacebookAIResearch开发。它提供了一系列高效的算法和数据结构，用于加速向量之间的相似性搜索，特别是在大规模数据集上。本文将介绍Faiss的原理、核心功能以及如何在实际项目中使用它。Faiss原理：近似最近邻搜索：Faiss的核心功能之一是近似最近邻搜索，它能够高效地在大规模数据集中找到与给定查询向量最相似的向量。这种搜索是近似的，
insert into select 主键自增_mybatis拦截器实现主键自动生成 weixin_39521651 insert into select 主键自增 mybatis delete返回值 mybatis insert返回主键 mybatis insert返回对象 mybatis plus insert返回主键 mybatis plus 插入生成id
前言前阵子和朋友聊天，他说他们项目有个需求，要实现主键自动生成，不想每次新增的时候，都手动设置主键。于是我就问他，那你们数据库表设置主键自动递增不就得了。他的回答是他们项目目前的id都是采用雪花算法来生成，因此为了项目稳定性，不会切换id的生成方式。朋友问我有没有什么实现思路，他们公司的orm框架是mybatis，我就建议他说，不然让你老大把mybatis切换成mybatis-plus。mybat
k均值聚类算法考试例题_k均值算法(k均值聚类算法计算题) 寻找你83497 k均值聚类算法考试例题
?算法：第一步：选K个初始聚类中心，z1(1),z2(1)，…，zK(1)，其中括号内的序号为寻找聚类中心的迭代运算的次序号。聚类中心的向量值可任意设定，例如可选开始的K个.k均值聚类：---------一种硬聚类算法，隶属度只有两个取值0或1，提出的基本根据是“类内误差平方和最小化”准则；模糊的c均值聚类算法：--------一种模糊聚类算法，是.K均值聚类算法是先随机选取K个对象作为初始的聚类
Python实现简单的机器学习算法 master_chenchengg python python 办公效率 python开发 IT
Python实现简单的机器学习算法开篇：初探机器学习的奇妙之旅搭建环境：一切从安装开始必备工具箱第一步：安装Anaconda和JupyterNotebook小贴士：如何配置Python环境变量算法初体验：从零开始的Python机器学习线性回归：让数据说话数据准备：从哪里找数据编码实战：Python实现线性回归模型评估：如何判断模型好坏逻辑回归：从分类开始理论入门：什么是逻辑回归代码实现：使用skl
推荐算法_隐语义-梯度下降 _feivirus_ 算法机器学习和数学推荐算法机器学习隐语义
importnumpyasnp1.模型实现"""inputrate_matrix:M行N列的评分矩阵，值为P*Q.P:初始化用户特征矩阵M*K.Q:初始化物品特征矩阵K*N.latent_feature_cnt:隐特征的向量个数max_iteration:最大迭代次数alpha:步长lamda:正则化系数output分解之后的P和Q"""defLFM_grad_desc(rate_matrix,l
K近邻算法_分类鸢尾花数据集 _feivirus_ 算法机器学习和数学分类机器学习 K近邻
importnumpyasnpimportpandasaspdfromsklearn.datasetsimportload_irisfromsklearn.model_selectionimporttrain_test_splitfromsklearn.metricsimportaccuracy_score1.数据预处理iris=load_iris()df=pd.DataFrame(data=ir
数据结构 | 栈和队列 TT-Kun 数据结构与算法数据结构栈队列 C语言
文章目录栈和队列1.栈：后进先出（LIFO）的数据结构1.1概念与结构1.2栈的实现2.队列：先进先出（FIFO）的数据结构2.1概念与结构2.2队列的实现3.栈和队列算法题3.1有效的括号3.2用队列实现栈3.3用栈实现队列3.4设计循环队列结论栈和队列在计算机科学中，栈和队列是两种基本且重要的数据结构，它们在处理数据存储和访问顺序方面有着独特的规则和应用。本文将详细介绍栈和队列的概念、结构、实
2024.9.6 Python，华为笔试题总结，字符串格式化，字符串操作，广度优先搜索解决公司组织绩效互评问题，无向图 RaidenQ python 华为 leetcode 算法力扣广度优先无向图
1.字符串格式化name="Alice"age=30formatted_string="Name:{},Age:{}".format(name,age)print(formatted_string)或者name="Alice"age=30formatted_string=f"Name:{name},Age:{age}"print(formatted_string)2.网络健康检查第一行有两个整数m
[Python] 数据结构详解及代码 AIAdvocate 算法 python 数据结构链表
今日内容大纲介绍数据结构介绍列表链表1.数据结构和算法简介程序大白话翻译,程序=数据结构+算法数据结构指的是存储,组织数据的方式.算法指的是为了解决实际业务问题而思考思路和方法,就叫:算法.2.算法的5大特性介绍算法具有独立性算法是解决问题的思路和方式,最重要的是思维,而不是语言,其(算法)可以通过多种语言进行演绎.5大特性有输入,需要传入1或者多个参数有输出,需要返回1个或者多个结果有穷性,执行
Python算法L5：贪心算法小熊同学哦 Python算法算法 python 贪心算法
Python贪心算法简介目录Python贪心算法简介贪心算法的基本步骤贪心算法的适用场景经典贪心算法问题1.**零钱兑换问题**2.**区间调度问题**3.**背包问题**贪心算法的优缺点优点：缺点：结语贪心算法（GreedyAlgorithm）是一种在每一步选择中都采取当前最优或最优解的算法。它的核心思想是，在保证每一步局部最优的情况下，希望通过贪心选择达到全局最优解。虽然贪心算法并不总能得到全
崩坏星穹铁道哪个角色值得培养崩坏星穹铁道新手角色优先级教学会飞滴鱼儿
崩坏星穹铁道新手角色培养攻略：哪些角色值得投资？在《崩坏星穹铁道》中，角色的强度和培养一直是玩家们关心的焦点。要想体验更爽快的游戏过程，选对角色至关重要。那么，哪些角色值得投资培养呢?本篇教学文章将针对新手玩家，从T0到T1强度的角色中为你做出详尽解析。游戏豹官网现在的手游平台很多，但是在游戏界有这么一个传说：“喜欢肝的玩家不如氪金玩家，氪金玩家不如内部福利玩家”，这就是游戏界可悲的生物链，很多平
【RabbitMQ 项目】服务端：数据管理模块之绑定管理月夜星辉雪 rabbitmq 分布式
文章目录一.编写思路二.代码实践一.编写思路定义绑定信息类交换机名称队列名称绑定关键字：交换机的路由交换算法中会用到没有是否持久化的标志，因为绑定是否持久化取决于交换机和队列是否持久化，只有它们都持久化时绑定才需要持久化。绑定就好像一根绳子，两端连接着交换机和队列，当一方不存在，它就没有存在的必要了定义绑定持久化类构造函数：如果数据库文件不存在则创建，打开数据库，创建binding_table插入
非对称加密算法原理与应用2——RSA私钥加密文件私语茶馆云部署与开发架构及产品灵感记录 RSA2048 私钥加密
作者：私语茶馆1.相关章节（1）非对称加密算法原理与应用1——秘钥的生成-CSDN博客第一章节讲述的是创建秘钥对，并将公钥和私钥导出为文件格式存储。本章节继续讲如何利用私钥加密内容，包括从密钥库或文件中读取私钥，并用RSA算法加密文件和String。2.私钥加密的概述本文主要基于第一章节的RSA2048bit的非对称加密算法讲述如何利用私钥加密文件。这种加密后的文件，只能由该私钥对应的公钥来解密。
粒子群优化 (PSO) 在三维正弦波函数中的应用 subject625Ruben 机器学习人工智能 matlab 算法
在这篇博客中，我们将展示如何使用粒子群优化（PSO）算法求解三维正弦波函数，并通过增加正弦波扰动，使优化过程更加复杂和有趣。本文将介绍目标函数的定义、PSO参数设置以及算法执行的详细过程，并展示搜索空间中的动态过程和收敛曲线。1.目标函数定义我们使用的目标函数是一个三维正弦波函数，定义如下：objectiveFunc=@(x)sin(sqrt(x(1).^2+x(2).^2))+0.5*sin(5
leetcode-617. 合并二叉树 manba_ leetcode hot100 leetcode 算法
题目描述给你两棵二叉树：root1和root2。想象一下，当你将其中一棵覆盖到另一棵之上时，两棵树上的一些节点将会重叠（而另一些不会）。你需要将这两棵树合并成一棵新二叉树。合并的规则是：如果两个节点重叠，那么将这两个节点的值相加作为合并后节点的新值；否则，不为null的节点将直接作为新二叉树的节点。返回合并后的二叉树。注意:合并过程必须从两个树的根节点开始。示例1：输入：root1=[1,3,2,
非对称加密算法————RSA理论及详情 hu19930613
转自：https://www.kancloud.cn/kancloud/rsa_algorithm/48484一、一点历史1976年以前，所有的加密方法都是同一种模式：（1）甲方选择某一种加密规则，对信息进行加密；（2）乙方使用同一种规则，对信息进行解密。由于加密和解密使用同样规则（简称"密钥"），这被称为"对称加密算法"（Symmetric-keyalgorithm）。这种加密模式有一个最大弱点
ai绘画工具midjourney怎么下载？附作品管理教程设计师早上好
Midjourney是一款功能强大的AI绘画工具，它使用机器学习技术和深度神经网络等算法，可以生成各种艺术风格的绘画作品。在创意设计、广告宣传等方面有着广泛的应用前景。那么，ai绘画工具midjourney怎么下载？本文将为您介绍Midjourney的下载以及作品的相关管理。一、Midjourney下载Midjourney的下载非常简单，只需打开Midjourney官网（点击“GetMidjour
【加密算法基础——对称加密和非对称加密】 XWWW668899 网络安全服务器笔记
对称加密与非对称加密对称加密和非对称加密是两种基本的加密方法，各自有不同的特点和用途。以下是详细比较：1.对称加密特点密钥:使用相同的密钥进行加密和解密。发送方和接收方必须共享这个密钥。速度:通常速度较快，适合处理大量数据。实现:算法相对简单，计算效率高。常见算法AES(高级加密标准)DES(数据加密标准)3DES(三重数据加密标准)RC4(流密码)应用场景文件加密磁盘加密传输大量数据时的加密2.
代码随想录Day 41|动态规划之买卖股票问题，leetcode题目121. 买卖股票的最佳时机、122. 买卖股票的最佳时机Ⅱ、123. 买卖股票的最佳时机Ⅲ LluckyYH 动态规划 leetcode 算法数据结构
提示：DDU，供自己复习使用。欢迎大家前来讨论~文章目录买卖股票的最佳时机相关题目题目一：121.买卖股票的最佳时机解题思路：题目二：122.买卖股票的最佳时机II解题思路：题目三：123.买卖股票的最佳时机III解题思路总结买卖股票的最佳时机相关题目题目一：121.买卖股票的最佳时机[[121.买卖股票的最佳时机](https://leetcode.cn/problems/combination
设计模式介绍 tntxia 设计模式
设计模式来源于土木工程师克里斯托弗亚历山大（http://en.wikipedia.org/wiki/Christopher_Alexander）的早期作品。他经常发表一些作品，内容是总结他在解决设计问题方面的经验，以及这些知识与城市和建筑模式之间有何关联。有一天，亚历山大突然发现，重复使用这些模式可以让某些设计构造取得我们期望的最佳效果。亚历山大与萨拉-石川佳纯和穆雷西乐弗斯坦合作
android高级组件使用(一) 百合不是茶 android RatingBar Spinner
1、自动完成文本框（AutoCompleteTextView） AutoCompleteTextView从EditText派生出来，实际上也是一个文本编辑框，但它比普通编辑框多一个功能：当用户输入一个字符后，自动完成文本框会显示一个下拉菜单，供用户从中选择，当用户选择某个菜单项之后，AutoCompleteTextView按用户选择自动填写该文本框。使用AutoCompleteTex
[网络与通讯]路由器市场大有潜力可挖掘 comsci 网络
如果国内的电子厂商和计算机设备厂商觉得手机市场已经有点饱和了,那么可以考虑一下交换机和路由器市场的进入问题..... 这方面的技术和知识,目前处在一个开放型的状态,有利于各类小型电子企业进入 &nbs
自写简单Redis内存统计shell 商人shang Linux shell 统计Redis内存
#!/bin/bash address="192.168.150.128:6666,192.168.150.128:6666" hosts=(${address//,/ }) sfile="staticts.log" for hostitem in ${hosts[@]} do ipport=(${hostitem
单例模式(饿汉 vs懒汉) oloz 单例模式
package 单例模式; /* * 应用场景:保证在整个应用之中某个对象的实例只有一个 * 单例模式种的《懒汉模式》 * */ public class Singleton { //01 将构造方法私有化，外界就无法用new Singleton()的方式获得实例 private Singleton(){}; //02 申明类得唯一实例 priva
springMvc json支持杨白白 json springmvc
1.Spring mvc处理json需要使用jackson的类库，因此需要先引入jackson包 2在spring mvc中解析输入为json格式的数据:使用@RequestBody来设置输入 @RequestMapping("helloJson") public @ResponseBody JsonTest helloJson() {
android播放，掃描添加本地音頻文件小桔子
最近幾乎沒有什麽事情，繼續鼓搗我的小東西。想在項目中加入一個簡易的音樂播放器功能，就像華為p6桌面上那麼大小的音樂播放器。用過天天動聽或者QQ音樂播放器的人都知道，可已通過本地掃描添加歌曲。不知道他們是怎麼實現的，我覺得應該掃描設備上的所有文件，過濾出音頻文件，每個文件實例化為一個實體，記錄文件名、路徑、歌手、類型、大小等信息。具體算法思想，
oracle常用命令 aichenglong oracle dba 常用命令
1 创建临时表空间 create temporary tablespace user_temp tempfile 'D:\oracle\oradata\Oracle9i\user_temp.dbf' size 50m autoextend on next 50m maxsize 20480m extent management local
25个Eclipse插件 AILIKES eclipse插件
提高代码质量的插件1. FindBugsFindBugs可以帮你找到Java代码中的bug，它使用Lesser GNU Public License的自由软件许可。2. CheckstyleCheckstyle插件可以集成到Eclipse IDE中去，能确保Java代码遵循标准代码样式。3. ECLemmaECLemma是一款拥有Eclipse Public License许可的免费工具，它提供了
Spring MVC拦截器+注解方式实现防止表单重复提交 baalwolf spring mvc
原理：在新建页面中Session保存token随机码，当保存时验证，通过后删除，当再次点击保存时由于服务器端的Session中已经不存在了，所有无法验证通过。 1.新建注解： ? 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
《Javascript高级程序设计(第3版)》闭包理解 bijian1013 JavaScript
“闭包是指有权访问另一个函数作用域中的变量的函数。”--《Javascript高级程序设计(第3版)》看以下代码： <script type="text/javascript"> function outer() { var i = 10; return f
AngularJS Module类的方法 bijian1013 JavaScript AngularJS Module
AngularJS中的Module类负责定义应用如何启动，它还可以通过声明的方式定义应用中的各个片段。我们来看看它是如何实现这些功能的。一.Main方法在哪里如果你是从Java或者Python编程语言转过来的，那么你可能很想知道AngularJS里面的main方法在哪里？这个把所
[Maven学习笔记七]Maven插件和目标 bit1129 maven插件
插件(plugin)和目标(goal) Maven，就其本质而言，是一个插件执行框架，Maven的每个目标的执行逻辑都是由插件来完成的，一个插件可以有1个或者几个目标，比如maven-compiler-plugin插件包含compile和testCompile，即maven-compiler-plugin提供了源代码编译和测试源代码编译的两个目标使用插件和目标使得我们可以干预
【Hadoop八】Yarn的资源调度策略 bit1129 hadoop
1. Hadoop的三种调度策略 Hadoop提供了3中作业调用的策略， FIFO Scheduler Fair Scheduler Capacity Scheduler 以上三种调度算法，在Hadoop MR1中就引入了，在Yarn中对它们进行了改进和完善.Fair和Capacity Scheduler用于多用户共享的资源调度 2. 多用户资源共享的调度
Nginx使用Linux内存加速静态文件访问 ronin47
Nginx是一个非常出色的静态资源web服务器。如果你嫌它还不够快，可以把放在磁盘中的文件，映射到内存中，减少高并发下的磁盘IO。先做几个假设。nginx.conf中所配置站点的路径是/home/wwwroot/res，站点所对应文件原始存储路径：/opt/web/res shell脚本非常简单，思路就是拷贝资源文件到内存中，然后在把网站的静态文件链接指向到内存中即可。具体如下：
关于Unity3D中的Shader的知识 brotherlamp unity unity资料 unity教程 unity视频 unity自学
首先先解释下Unity3D的Shader，Unity里面的Shaders是使用一种叫ShaderLab的语言编写的，它同微软的FX文件或者NVIDIA的CgFX有些类似。传统意义上的vertex shader和pixel shader还是使用标准的Cg/HLSL 编程语言编写的。因此Unity文档里面的Shader，都是指用ShaderLab编写的代码，然后我们来看下Unity3D自带的60多个S
CopyOnWriteArrayList vs ArrayList bylijinnan java
package com.ljn.base; import java.util.ArrayList; import java.util.Iterator; import java.util.List; import java.util.concurrent.CopyOnWriteArrayList; /** * 总述： * 1.ArrayListi不是线程安全的，CopyO
内存中栈和堆的区别 chicony 内存
1、内存分配方面：堆：一般由程序员分配释放，若程序员不释放，程序结束时可能由OS回收。注意它与数据结构中的堆是两回事，分配方式是类似于链表。可能用到的关键字如下：new、malloc、delete、free等等。栈：由编译器(Compiler)自动分配释放，存放函数的参数值，局部变量的值等。其操作方式类似于数据结构中
回答一位网友对Scala的提问 chenchao051 scala map
本来准备在私信里直接回复了，但是发现不太方便，就简要回答在这里。问题写道对于scala的简洁十分佩服，但又觉得比较晦涩，例如一例，Map("a" -> List(11,111)).flatMap(_._2)，可否说下最后那个函数做了什么，真正在开发的时候也会如此简洁？谢谢先回答一点，在实际使用中，Scala毫无疑问就是这么简单。
mysql 取每组前几条记录 daizj mysql 分组最大值最小值每组三条记录
一、对分组的记录取前N条记录：例如：取每组的前3条最大的记录 1.用子查询： SELECT * FROM tableName a WHERE 3> (SELECT COUNT(*) FROM tableName b WHERE b.id=a.id AND b.cnt>a. cnt) ORDER BY a.id,a.account DE
HTTP深入浅出 http请求 dcj3sjt126com http
HTTP(HyperText Transfer Protocol)是一套计算机通过网络进行通信的规则。计算机专家设计出HTTP，使HTTP客户（如Web浏览器）能够从HTTP服务器(Web服务器)请求信息和服务，HTTP目前协议的版本是1.1.HTTP是一种无状态的协议，无状态是指Web浏览器和Web服务器之间不需要建立持久的连接，这意味着当一个客户端向服务器端发出请求，然后We
判断MySQL记录是否存在方法比较 dcj3sjt126com mysql
把数据写入到数据库的时，常常会碰到先要检测要插入的记录是否存在，然后决定是否要写入。　　我这里总结了判断记录是否存在的常用方法：　　sql语句： select count ( * ) from tablename; 　　然后读取count(*)的值判断记录是否存在。对于这种方法性能上有些浪费，我们只是想判断记录记录是否存在，没有必要全部都查出来。
对HTML XML的一点认识 e200702084 html xml
感谢http://www.w3school.com.cn提供的资料 HTML 文档中的每个成分都是一个节点。节点根据 DOM，HTML 文档中的每个成分都是一个节点。 DOM 是这样规定的：整个文档是一个文档节点每个 HTML 标签是一个元素节点包含在 HTML 元素中的文本是文本节点每一个 HTML 属性是一个属性节点注释属于注释节点 Node 层次
jquery分页插件 genaiwei jquery Web 前端分页插件
//jquery页码控件// 创建一个闭包 (function($) { // 插件的定义 $.fn.pageTool = function(options) { var totalPa
Mybatis与Ibatis对照入门于学习 Josh_Persistence mybatis ibatis 区别联系
一、为什么使用IBatis/Mybatis 对于从事 Java EE 的开发人员来说，iBatis 是一个再熟悉不过的持久层框架了，在 Hibernate、JPA 这样的一站式对象 / 关系映射（O/R Mapping）解决方案盛行之前，iBaits 基本是持久层框架的不二选择。即使在持久层框架层出不穷的今天，iBatis 凭借着易学易用、
C中怎样合理决定使用那种整数类型？秋风扫落叶 c 数据类型
如果需要大数值(大于32767或小于32767), 使用long 型。否则, 如果空间很重要 (如有大数组或很多结构), 使用 short 型。除此之外, 就使用 int 型。如果严格定义的溢出特征很重要而负值无关紧要, 或者你希望在操作二进制位和字节时避免符号扩展的问题, 请使用对应的无符号类型。但是, 要注意在表达式中混用有符号和无符号值的情况。 &nbs
maven问题 zhb8015 maven问题
问题1： Eclipse 中新建maven项目无法添加src/main/java 问题 eclipse创建maevn web项目，在选择maven_archetype_web原型后，默认只有src/main/resources这个Source Floder。按照maven目录结构，添加src/main/ja
(二)androidpn-server tomcat版源码解析之--push消息处理 spjich java androdipn 推送
在 (一)androidpn-server tomcat版源码解析之--项目启动这篇中，已经描述了整个推送服务器的启动过程，并且把握到了消息的入口即XmppIoHandler这个类，今天我将继续往下分析下面的核心代码，主要分为3大块，链接创建，消息的发送，链接关闭。先贴一段XmppIoHandler的部分代码 /** * Invoked from an I/O proc
用js中的formData类型解决ajax提交表单时文件不能被serialize方法序列化的问题中华好儿孙 JavaScript Ajax Web 上传文件 FormData
var formData = new FormData($("#inputFileForm")[0]); $.ajax({ type:'post', url:webRoot+"/electronicContractUrl/webapp/uploadfile", data:formData, async: false, ca
mybatis常用jdbcType数据类型 ysj5125094 mybatis mapper jdbcType
MyBatis 通过包含的jdbcType 类型 BIT FLOAT CHAR