✅作者简介:热爱科研的Matlab仿真开发者,修心和技术同步精进,matlab项目合作可私信。
个人主页:Matlab科研工作室
个人信条:格物致知。
更多Matlab完整代码及仿真定制内容点击
智能优化算法 神经网络预测 雷达通信 无线传感器 电力系统
信号处理 图像处理 路径规划 元胞自动机 无人机
内容介绍
在机器学习和人工智能领域,时间序列数据的回归预测是一个重要的问题。长短期记忆(LSTM)是一种广泛应用于处理时间序列数据的递归神经网络(RNN)架构。然而,LSTM模型的性能高度依赖于其超参数的选择,这使得模型的调优变得非常困难。为了解决这个问题,我们可以使用贝叶斯优化来自动地找到最佳的超参数配置。
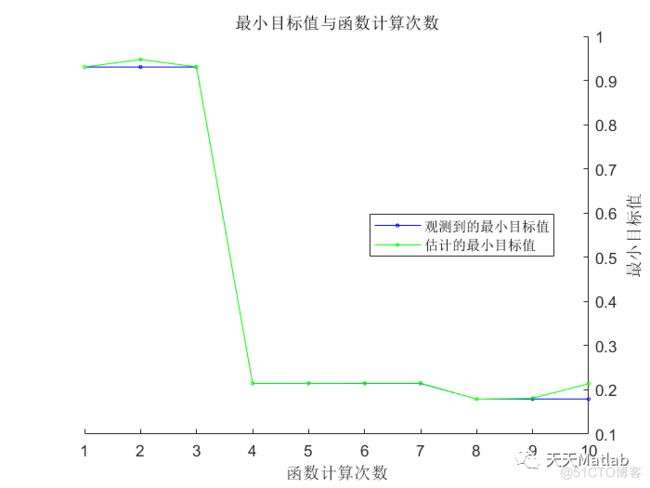
贝叶斯优化是一种通过在搜索空间中选择合适的候选点来优化目标函数的方法。它通过建立一个代理模型来估计目标函数的性能,并使用这个模型来指导搜索过程。在这种情况下,我们可以使用贝叶斯优化来搜索LSTM模型的超参数配置,以最大化回归预测的准确性。
BO-LSTM是一种基于贝叶斯优化的LSTM模型,它结合了贝叶斯优化和LSTM模型的优势。BO-LSTM的核心思想是通过贝叶斯优化来选择LSTM模型的超参数配置,并使用这些配置来训练和预测时间序列数据。通过迭代地使用贝叶斯优化算法,BO-LSTM可以逐步改进模型的性能,从而实现更准确的回归预测。
为了实现BO-LSTM模型,我们需要定义LSTM模型的超参数空间和目标函数。超参数空间包括LSTM的隐藏层大小、学习率、迭代次数等。目标函数可以是回归预测的均方根误差(RMSE)或平均绝对误差(MAE)。贝叶斯优化算法将在超参数空间中选择候选点,并使用目标函数来评估它们的性能。通过迭代地选择候选点并更新代理模型,贝叶斯优化算法可以逐步改进模型的性能。
BO-LSTM的优点是它可以自动地找到最佳的超参数配置,而无需手动调优。这使得模型的训练和预测过程更加高效和准确。此外,BO-LSTM还可以适应不同的时间序列数据,并在不同的问题上取得良好的性能。
然而,BO-LSTM也有一些限制。首先,贝叶斯优化算法的计算成本较高,特别是在超参数空间较大的情况下。其次,BO-LSTM的性能高度依赖于目标函数的选择和超参数空间的定义。因此,在使用BO-LSTM之前,我们需要仔细选择目标函数和超参数空间,以确保取得最佳的结果。
总结起来,基于贝叶斯优化的长短期记忆BO-LSTM模型是一种强大的工具,用于时间序列数据的回归预测。它通过自动选择最佳的超参数配置来提高模型的性能,并在实践中取得了良好的效果。然而,我们仍然需要注意BO-LSTM的局限性,并根据具体问题的需求进行合理的调整和改进。
部分代码
%% Example 'GpsMultiCorrelator' #3: Generation of energy matrices resulting from non-coherent integrations with different periods
%
% Generation of energy matrices resulting from the accumulation of non-coherent correlation results, over different periods, between:
% - A received signal including a GPS signal,
% - A local signal matching in terms of PRN, Doppler and code phase.
% Parameters
SamplingPeriod = 100e-9;
CarrierFrequency = 0;
PRN = 3;
CN0 = 45*10;
Doppler = 0;
CodePhase = 0;
Duration = 25e-3;
% Creation of 'GpsSignals' object
GPS = ...
GpsSignals('SamplingPeriod', SamplingPeriod,...
'CarrierFrequency', CarrierFrequency,...
'NextValues', 'replace',...
'PRN', PRN,...
'CN0', CN0,...
'Doppler', Doppler,...
'CodePhase', CodePhase);
% Creation of 'GpsMultiCorrelator' object
MultiCorrelator = ...
GpsMultiCorrelator('SamplingPeriod', SamplingPeriod,...
'CarrierFrequency', CarrierFrequency,...
'FilterFrequencies', -4000:500:+4000-500,...
'CorrelatorCodePhases', -4:0.5:+4-0.5,...
'PRN', PRN,...
'Doppler', Doppler,...
'CodePhase', CodePhase,...
'CodePhaseIncrement', 0,...
'NonCoherentIntegrationPeriod', 5e-3);
for n = 1:6
% Signal duration/non-coherent integration period
Duration = n*5e-3;
% Update of GPS signals
GPS.update('Duration',Duration);
% Setting of non-coherent integration period
MultiCorrelator.set('NonCoherentIntegrationPeriod',Duration);
% Correlation
MultiCorrelator.correlate(GPS.Values);
end
% Figure
Figure = ...
figure('Color','w','Name','');
Axes = subplot(4,1,1:3,'Parent', Figure,'NextPlot','Add');
% Display of energy matrices
M = numel(MultiCorrelator.EnergyMatrices);
for m = 1:M
[CorrelatorCodePhases_,FilterFrequencies_] = meshgrid(MultiCorrelator.EnergyMatrices(m).CodePhases,MultiCorrelator.EnergyMatrices(m).Frequencies);
surf(Axes,CorrelatorCodePhases_,FilterFrequencies_,MultiCorrelator.EnergyMatrices(m).Matrix,MultiCorrelator.EnergyMatrices(m).Matrix,...
'FaceColor','Interp','EdgeAlpha',0.75,'FaceAlpha',(M-m+1)/(M+1));
end
% Display of maximum
Maxima = cellfun(@(M)max(M,[],'all'),{MultiCorrelator.EnergyMatrices.Matrix});
m = find(eq(Maxima,max(Maxima)));
[i,j] = find(eq(MultiCorrelator.EnergyMatrices(m).Matrix,Maxima(m)));
text(MultiCorrelator.EnergyMatrices(m).CodePhases(j),MultiCorrelator.EnergyMatrices(m).Frequencies(i),MultiCorrelator.EnergyMatrices(m).Matrix(i,j),...
{'Energy maximum',...
sprintf('MultiCorrelator #%u: %+.fchip',j,MultiCorrelator.EnergyMatrices(m).CodePhases(j)),...
sprintf('Filter #%u: %+.fHz',i,MultiCorrelator.EnergyMatrices(m).Frequencies(i)),...
'\downarrow'},...
'HorizontalAlignment','center',...
'VerticalAlignment', 'bottom');
% Display of informations
view(Axes,-30,30);
T = [MultiCorrelator.EnergyMatrices(:).IntegrationTime];
title({'Energy matrices',...
sprintf('(%u matrices x %u filters x %u correlators,',...
numel(MultiCorrelator.EnergyMatrices),...
numel(MultiCorrelator.EnergyMatrices(1).Frequencies),...
numel(MultiCorrelator.EnergyMatrices(1).CodePhases)),...
sprintf('integration period: %s %sms)',num2str(1e3*T(1:end-1),'%.f, '),num2str(1e3*T(end),'%.f'))});
xlabel('Code phase [chip]');
ylabel('Frequency [Hz]');
zlabel(sprintf('Energy - PRN%u',PRN));
% Colorbar
Map = hsv;
Map = Map(1:find(diff(Map(:,1))>0,1,'first'),:);
Map = [Map;0 0 1];
colormap(fliplr(Map));
Colorbar = colorbar;
Colorbar.Label.String = 'Energy';
Colorbar.Location = 'EastOutside';
% Display of maxima
Axes(2) = subplot(4,1,4,'Parent',Figure,'NextPlot','Add','Box','on','Xgrid','on','Ygrid','on');
plot(Axes(2),1e3*T,Maxima,'.-');
set(Axes(2),'Xlim',[min(1e3*T) max(1e3*T)]);
title('Energy maximum vs non-coherent integration period')
xlabel('Non-coherent integration period [ms]');
ylabel('Energy maximum');
% Update of axes
set([Axes';findall(Axes,'type','text')],'fontsize',9);
% Main title
sgtitle('Energy matrices and non-coherent integration period',...
'FontSize',11,'FontWeight','Bold');
% Maximization of figure
Figure.WindowState = 'maximized';⛳️ 运行结果
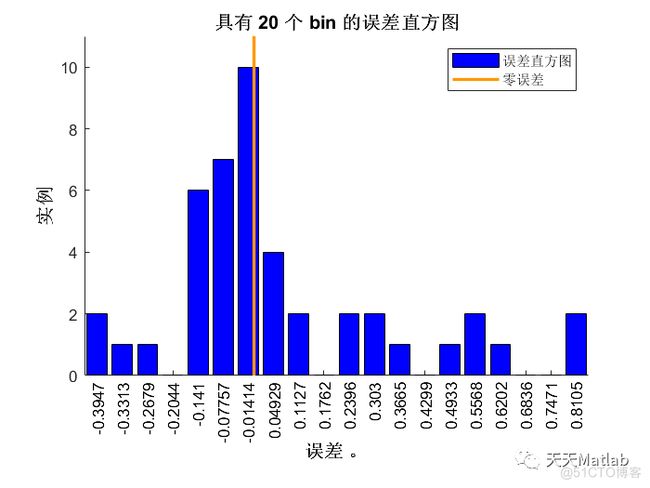
-----------------------误差计算--------------------------
评价结果如下所示:
平均绝对误差MAE为:0.19772
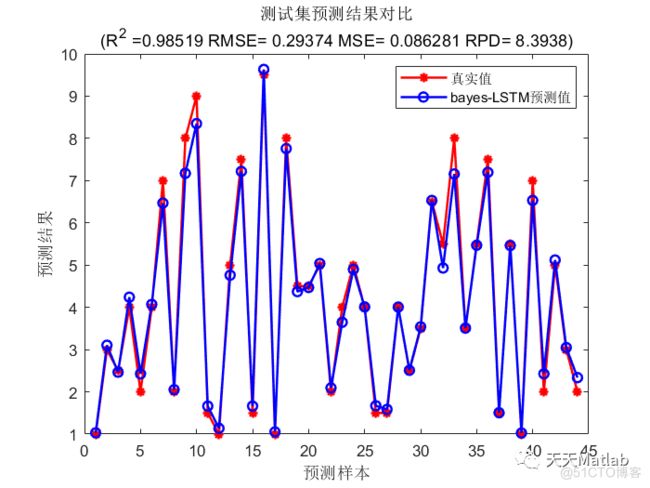
均方误差MSE为: 0.086281
均方根误差RMSEP为: 0.29374
决定系数R^2为: 0.98519
剩余预测残差RPD为: 8.3938
平均绝对百分比误差MAPE为: 0.053654