数据结构 - 4(栈和队列6000字详解)
一:栈
1.1 栈的概念
栈:一种特殊的线性表,其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶,另一端称为栈底。栈中的数据元素遵守后进先出LIFO(Last In First Out)的原则。
- 压栈(push):栈的插入操作叫做进栈/压栈/入栈,入数据在栈顶。
- 出栈(pop):栈的删除操作叫做出栈。出数据在栈顶。
1.2 栈的使用
| 方法 | 功能 |
|---|---|
| Stack() | 构造一个空的栈 |
| E push(E e) | 将e入栈,并返回e |
| E pop() | 将栈顶元素出栈并返回 |
| E peek() | 获取栈顶元素 |
| int size() | 获取栈中有效元素个数 |
| boolean empty() | 检测栈是否为空 |
下面是这些方法的使用示例:
public static void main(String[] args) {
Stack<Integer> s = new Stack();
s.push(1);
s.push(2);
s.push(3);
s.push(4);
System.out.println(s.size()); // 获取栈中有效元素个数---> 4
System.out.println(s.peek()); // 获取栈顶元素---> 4
s.pop(); // 4出栈,栈中剩余1 2 3,栈顶元素为3
System.out.println(s.pop()); // 3出栈,栈中剩余1 2 栈顶元素为3
if(s.empty()){
System.out.println("栈空");
}else{
System.out.println(s.size());
}
}
1.3栈的模拟实现

从上图中可以看到,Stack继承了Vector,Vector和ArrayList类似,都是动态的顺序表,不同的是Vector是线程安全的。
public class MyStack {
int[] array; // 数组用于存储栈元素
int size; // 记录栈中元素的个数
// 构造方法,创建一个初始容量为3的数组作为栈的存储空间
public MyStack(){
array = new int[3];
}
// 入栈操作,将元素 e 加入到栈顶,并返回入栈的元素
public int push(int e){
ensureCapacity();// 确保栈的容量足够
array[size++] = e;// 将元素 e 加入到数组中,更新 size 的值
return e;// 返回入栈的元素
}
// 出栈操作,将栈顶元素移出并返回该元素
public int pop(){
int e = peek(); // 调用 peek 方法获取栈顶元素,并记录在变量 e 中
size--; // 栈中元素个数减少1
return e;// 返回出栈的元素
}
// 返回栈顶元素的值,但不删除栈顶元素
public int peek(){
if(empty()){ // 如果栈为空,则抛出异常
throw new RuntimeException("栈为空,无法获取栈顶元素");
}
return array[size-1];// 返回栈顶元素的值
}
// 返回栈中元素的个数
public int size(){
return size;
}
// 判断栈是否为空
public boolean empty(){
return 0 == size;
}
// 确保栈的容量足够,如果栈已满,则将栈的容量扩大为原来的2倍
private void ensureCapacity(){
if(size == array.length){
array = Arrays.copyOf(array, size*2);
}
}
}
二:队列
2.1 队列的概念
队列:只允许在一端进行插入数据操作,在另一端进行删除数据操作的特殊线性表,队列具有先进先出FIFO(FirstIn First Out) 入队列:进行插入操作的一端称为队尾(Tail/Rear) 出队列:进行删除操作的一端称为队头(Head/Front)
2.2 队列的使用
在Java中,Queue是个接口,底层是通过链表实现的。

下面是队列中常用的方法:
| 方法 | 功能 |
|---|---|
| boolean offer(E e) | 入队列 |
| E poll() | 出队列 |
| peek() | 获取队头元素 |
| int size() | 获取队列中有效元素个数 |
| boolean isEmpty() | 检测队列是否为空 |
注意:
- Queue是个接口,在实例化时必须实例化LinkedList的对象,因为LinkedList实现了Queue接口。
下面是这些方法的使用示例:
public static void main(String[] args) {
Queue<Integer> q = new LinkedList<>();
// 从队尾入队列
q.offer(1);
q.offer(2);
q.offer(3);
q.offer(4);
q.offer(5);
System.out.println(q.size());
// 获取队头元素
System.out.println(q.peek());
q.poll();
System.out.println(q.poll()); // 从队头出队列,并将删除的元素返回
if(q.isEmpty()){
System.out.println("队列空");
}else{
System.out.println(q.size());
}
}
2.3队列的模拟实现
队列中既然可以存储元素,那底层肯定要有能够保存元素的空间,通过前面线性表的学习了解到常见的空间类型有两种:顺序结构 和 链式结构。所以队列的实现也可以采用这两种方式,但是具体采用哪种实现方式取决于具体的需求和场景。
-
顺序结构:使用数组或列表等连续的内存空间来存储队列元素。顺序结构实现队列的优点是简单、易于理解和实现,并且访问元素的时间复杂度为 O(1)。缺点是在插入和删除操作时可能需要进行元素的搬移,这会造成时间复杂度为 O(n)。
-
链式结构:使用链表的形式来存储队列元素。链式结构实现队列的优点是插入和删除操作的时间复杂度为 O(1),无需进行元素的搬移。缺点是需要额外的指针来维护节点之间的连接,且节点的分配和释放可能会引起额外的内存开销和碎片问题。
所以说如果你以访问为主,那么采用顺序结构,如果你以插入和删除为主,那么采用链式结构
2.3.1顺序结构实现队列
因为我以及在代码中通过注释进行了详细的解答,在此就不过多赘述了。
public class Queue {
private int capacity; // 队列的容量
private int[] elements; // 存储队列元素的数组
private int front; // 队列的头指针
private int rear; // 队列的尾指针
private int size; // 队列的当前大小
// 队列的构造方法
public Queue(int capacity) {
this.capacity = capacity;
this.elements = new int[capacity];
this.front = 0;
this.rear = -1;
this.size = 0;
}
// 入队列---向队尾插入新元素
public void offer(int element) {
// 检查队列是否已满
if (size == capacity) {
throw new IllegalStateException("Queue is full");
}
// 队尾指针移动到下一个位置
rear = (rear + 1) % capacity;
// 将新元素插入队尾
elements[rear] = element;
// 队列大小加1
size++;
}
// 出队列---将队头元素删除并返回
public int poll() {
// 检查队列是否为空
if (isEmpty()) {
throw new IllegalStateException("Queue is empty");
}
// 获取队头元素
int element = elements[front];
// 队头指针移动到下一个位置
front = (front + 1) % capacity;
// 队列大小减1
size--;
// 返回队头元素
return element;
}
// 获取队头元素---返回队头元素的值,但不删除
public int peek() {
// 检查队列是否为空
if (isEmpty()) {
throw new IllegalStateException("Queue is empty");
}
// 返回队头元素
return elements[front];
}
// 返回队列的大小
public int size() {
return size;
}
// 判断队列是否为空
public boolean isEmpty() {
return size == 0;
}
}
2.3.2链式结构实现队列
public class Queue {
// 双向链表节点
public static class ListNode{
ListNode next;
ListNode prev;
int value;
// 双向链表节点的构造方法
ListNode(int value){
this.value = value;
}
}
ListNode first; // 队头
ListNode last; // 队尾
int size = 0;
// 入队列---向双向链表尾部插入新节点
public void offer(int e){
ListNode newNode = new ListNode(e);
if (first == null) {
// 如果队列为空,新节点同时成为队头和队尾
first = newNode;
} else {
// 如果队列不为空,将新节点插入到队尾
last.next = newNode;
newNode.prev = last;
}
// 更新队尾为新节点
last = newNode;
// 队列大小加1
size++;
}
// 出队列---将双向链表第一个节点删除
public int poll(){
// 队列为空,返回null
if (first == null) {
return null;
} else if (first == last) {
// 队列中只有一个元素,将队头和队尾设置为null即可
last = null;
first = null;
} else {
// 队列中有多个元素,将第一个节点删除
int value = first.value;
first = first.next;
// 删除节点的引用关系,避免内存泄漏
first.prev.next = null;
first.prev = null;
return value;
}
// 队列大小减1
--size;
// 返回删除的值
return value;
}
// 获取队头元素---获取双向链表的第一个节点的值
public int peek(){
// 如果队列为空,返回null
if (first == null) {
return null;
}
// 返回队头的值
return first.value;
}
// 返回队列的大小
public int size() {
return size;
}
// 判断队列是否为空
public boolean isEmpty(){
return first == null;
}
}
2.4 循环队列
2.4.1索引公式
循环队列的视图如下:
我们该如何去实现一个循环队列呢?答案是通过 %取模
举个例子:
int a = b % 7;
在这个例子中,我们不管b取何值,a的取值返回是不是始终在0到6之间,所以我们通过这个性质就可以很好的把队列的首和尾建立关联,即尾向后走一步就到了头,因此我们就可以很好的去实现一个循环队列了
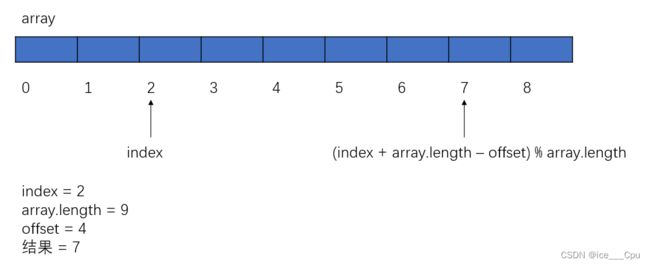
在循环队列中,(index + offset) % array.length 和 (index + array.length - offset) % array.length 是我们常用的索引计算方式。其中:
index是当前元素的索引。offset是偏移量,它决定了要添加/访问的元素在当前索引的基础上偏移了多少个位置。array.length是数组的长度,它表示整个循环队列的大小。
下面我们对这两个公式进行解释:
(index + offset) % array.length:- 当我们需要向循环队列的下一个位置插入元素时,我们使用这种索引计算方式。
- 假设队列在索引5处结束,我们需要向后移动1个位置,即在索引7处插入元素。使用
(5 + 1) % 8,得到的值是6,即有效的索引。
(index + array.length - offset) % array.length:- 当我们需要从循环队列的上一个位置移除元素时,我们使用这种索引计算方式。
- 假设队列在索引2处结束,我们需要向前移动1个位置,即从索引1处移除元素。使用
(2 + 8 - 1) % 8,得到的值是1,即有效的索引。
这两种计算方式都确保了索引在循环队列中的有效范围内,因为它们会通过取模运算将索引限制在数组长度范围内。这样,我们可以在循环队列中正确地插入和移除元素。
2.4.2 队列区分空和满
当我们使用一个固定大小的数组作为队列的底层数据结构。在循环队列中,我们使用两个指针,一个指向队列的头部,即出队列的位置,另一个指向队列的尾部,即入队列的位置。
当队列为空时,这两个指针指向同一个位置,即头部与尾部指针相等。而当队列满时,尾部指针的下一个位置就是头部指针所在的位置。
那么我们该怎么区分队列是空还是满呢?
为了区分队列是空还是满,我们可以采用三种常用的方法:
- 使用 size 属性记录:
通过添加一个 size 属性来记录队列中的元素数量,可以方便地判断队列是空还是满。当队列为空时,size 的值为 0,当队列满时,size 的值等于队列的容量。
- 保留一个位置:
在循环队列的实现中,可以将一个位置始终空置不用,用于区分队列是空还是满。例如,当队列为空时,头部指针和尾部指针都指向同一个位置;当队列满时,尾部指针的下一个位置就是头部指针所在的位置。通过查看这个空置位置是否为空,可以判断队列是空还是满。
- 使用标记:
可以在循环队列中使用一个额外的标记来区分队列是空还是满。这个标记可以是一个布尔值或者一个特殊的值,用于表示队列的状态。例如,当队列为空时,可以将标记设置为 true;当队列满时,可以将标记设置为 false。通过判断标记的值,可以确定队列的状态。
这些方法都可以用于区分队列是空还是满,具体选择哪种方法取决于个人偏好和实际需求。
2.5 Deque双端队列
双端队列(deque)是指允许两端都可以进行入队和出队操作的队列,deque 是 “double ended queue” 的简称。那就说明元素可以从队头出队和入队,也可以从队尾出队和入队。

Deque是一个接口,使用时必须创建LinkedList的对象。

在实际工程中,使用Deque接口是比较多的,栈和队列均可以使用该接口。
Deque<Integer> stack = new ArrayDeque<>();//双端队列的线性实现
Deque<Integer> queue = new LinkedList<>();//双端队列的链式实现