手撕排序之快速排序

快排的思想（霍尔版本）：

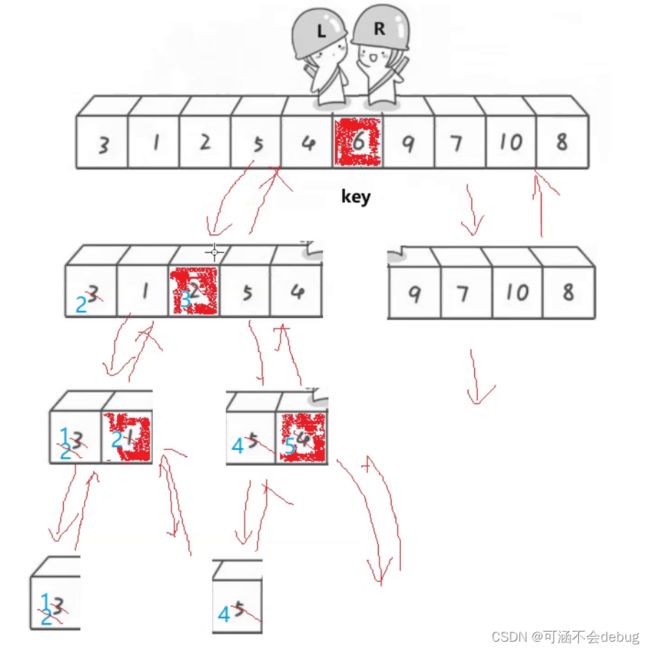
如何实现单趟排序：

先假设key是数列的首元素，然后分别定义left和right，left指向首元素的下一个元素，right指向最后一个元素。

先遍历右边，如果比key小，就停止遍历，如果比key大就right--；注意这是一个while循环

当右边的while循环停止时，进行左边的遍历，如果比key小就left++，如果大就停止记录这个下标。（这也是一个while循环）

当两个while循环都终止时，将left位置的值和right位置的值进行交换。

最后当left和right相等时，注意此时两个相同的下标指向的值与key交换，因为该值一定小于key。

单趟排序完成！

该单趟排序的意义：

key元素已经正确到达位置，因为左边都是比他小的元素，右边都是比他大的元素。

单趟排序过后，只有key元素到达了指定位置，我们如何让key左边和右边的元素也一样排好序呢？

这时候我们可以采用二叉树分治的思想，左边也一样找出key，重复相同的算法步骤，右边同样，

控制左右的数据范围

直到分割到只有一个元素为止，这样排序就完成啦。

解答疑问：

为什么最后left和right的值指向同一个元素，那个元素一定小于key元素的值？

（相遇位置的元素为什么一定比key小）

右边先走做到的！

分析两种相遇的情况：

1. R动L不动，去跟L相遇：相遇位置是L的位置。L和R在上一轮交换过，交换以后L 的位置比key小。
2. L动R不动，去跟R相遇：R先走，找大比key小的，已经停下来，这是L找大没有找到，跟R相遇了，相遇位置比key小。

总而言之，不论哪种相遇情况，相遇的位置总是比key小。

利用递归思路实现快排的一些坑点：

1. 找大和找小的判断条件容易出错。如果不写等号，left和right的值都可能指向等于key的元素，导致一直无效交换key，造成死循环。加上等号后，还要加上判断条件左值要小于右值，以免极端条件出现，一直--或++，造成越界
2. 最后交换key元素的值，我们应该记录key元素的下标，而不是key，因为key只是一个局部变量，交换key的值并不影响数组中的顺序。

利用递归思路实现快排

优化版本：（三数取中）

该快排在理想的情况下，时间复杂度是O(N*logN)。

何为理想状态？

每次key的值大小顺序都在数列的中间左右

就是最后key每次交换元素都在数列的中间，明显的二分，也就造成了logN的算法。

但也有可能key的值很极端，在两头，如果每次都这样，（基本有序的情况）算法就变成了N^2.

为了尽量避免这种情况出现，我们为key加上一层保险，尽量保证key的值不是那么极端。

下面加上三数取中的算法~

优化版本代码：

//三数取中
int GetMidi(int* a, int left, int right)
{
	int mid = (left + right) / 2;
	if (a[left] < a[mid])
	{
		if (a[right] > a[mid])
			return mid;
		else
		{
			if (a[left] < a[right])
				return right;
			else
				return left;
		}
	}
	else
	{
		if (a[right] < a[mid])
			return mid;
		else
		{
			if (a[left] > a[right])
				return right;
			else
				return left;
		}
	}
}


int PartSort1(int* a, int left, int right)
{
	int midi = GetMidi(a, left, right);
	Swap(&a[midi], &a[left]);
	int keyi = left;
	while (left= a[keyi])
		{
			right--;
		}
		//再从左边找大
		while (left < right && a[left] <= a[keyi])
		{
			left++;
		}
		Swap(&a[left], &a[right]);
	}
	Swap(&a[keyi], &a[left]);
	return left;
}

//利用递归的思路实现
void QuickSort(int* a, int left, int right)
{
	if (left >= right)
		return;
	int mid = PartSort1(a, left, right);
	QuickSort(a, left, mid - 1);
	QuickSort(a, mid + 1, right);
}

实现挖坑法：

挖坑法本质上与递归是一个思路，只不过在思想上做了优化。

有人觉得上一个方法难以理解，不知道为何最后交换的值一定比key小。

所以诞生了挖坑法。

所谓挖坑法，也是先从左边找到一个key，取出key元素，使得key位置形成一个坑，从右边开始遍历，当比key小时，就将右边的值填左边的坑位，此时右边又形成一个坑位，再从左边遍历，找到比key大的，填到右边的坑位，左边又形成了坑位，以此类推……

直到左右遍历到同一个坑位时，将最先取出key的元素放到这个坑位，这样，单趟排序就完成了，然后也是递归，形成完整的排序。

总结挖坑法是上一个方法的思想的一个优化~

挖坑法代码：

// 快速排序挖坑法
int PartSort2(int* a, int left, int right)
{
	//记录洞的下标
	int midi = GetMidi(a, left, right);
	Swap(&a[midi], &a[left]);
	int holei = left;
	//记录需要排序元素的值
	int ret = a[left];
	while (left < right)
	{
		//右边先走，找小，填到左边的坑，右边形成新的坑位
		while (left < right && a[right] >= ret)
		{
			right--;
		}
		a[holei] = a[right];
		holei = right;
		//左边再走，找大，填到右边的坑，左边形成新的坑位
		while (left < right && a[left] <= ret)
		{
			left++;
		}
		a[holei] = a[left];
		holei = left;
	}
	a[holei] = ret;
	return holei;
}

前后指针法：

前后指针法也是递归这条路上衍生出的新思想。

总体思路：

定义前后指针，cur和prev，前指针prev指向key元素，然后cur元素指向key元素的下一个元素

cur先走，无论cur下标指向元素大小是大于还是小于key元素，cur都要向后遍历。

但对于prev前指针，如果cur指向的元素大于key，prev不动，如果cur指向的元素小于key元素，

若小于，则prev指针先向后移一位，并与cur指向的内容与prev指向的内容交换，然后cur指针++。

最后循环结束的条件就是cur指针指向的元素已经超出数列范围，然后将prev指向的元素与key交换。

为何prev指向的元素一定比key元素小？

因为prev当前指向的元素已经是交换过的，之前是cur指向的元素比key小。

本质是把一段大于key的区间，推箱子似的往右推，同时小的甩到左边去。

原码：

//快速排序前后指针法
int PartSort3(int* a, int left, int right)
{
	int midi = GetMidi(a, left, right);
	Swap(&a[left], &a[midi]);
	int key = a[left];
	int prev = left;
	int cur = left + 1;
	while (cur <= right)
	{
		if (a[cur] < key)
		{
			prev++;
			Swap(&a[prev], &a[cur]);
		}
		cur++;
	}
	Swap(&a[left], &a[prev]);
	return prev;
}

上面介绍了利用递归完成快排的三种思想，下面来介绍非递归算法实现快排。

---

利用非递归完成快排

思想：

因为递归函数中的栈帧是创建在操作系统中的栈上，而栈上的空间较小，一般递归5000次左右，就会报错——StackOverflow（经典的栈溢出错误），所以我们不能过于依赖递归，我们还需要掌握如何将一个递归的算法转换成非递归的算法。

思路：

我们用非递归写程序时，一般会借助到数据结构中的栈和队列，此次我们利用栈来完成非递归的快排。

提醒：

我们只需要知道数列的下标，就可以进行单趟排序，所以压栈和出栈的操作对象就是数列的两个元素的下标，并不是将整个数列进行压栈！

我们需要将数列的首元素和尾元素的下标压栈，然后分别出栈，使这两个元素作为partsort的参数，接着返回keyi元素，也就是下标，接着再压栈[left,keyi-1]  [keyi+1,right]，直到栈为空，循环结束。

原码：

void QuickSortNonR(int* a, int left, int right)
{
	//注意操作的都是下标
	ST st;
	SLInit(&st);
	STPush(&st, right);
	STPush(&st, left);
	while (!STEmpty(&st))
	{
		int begin = STTop(&st);
		STPop(&st);
		int end = STTop(&st);
		STPop(&st);
		int keyi = PartSort1(a, begin, end);
		//[left,keyi-1]  [keyi+1,right]
		//根据栈的特性，想要从左到右遍历，我们先放右区间，再放左区间
		if (keyi+1 < end)
		{
			STPush(&st, right);
			STPush(&st, keyi + 1);
		}
		if (keyi-1 > begin)
		{
			STPush(&st, keyi - 1);
			STPush(&st, left);
		}
	}
	SLDestroy(&st);
}