数据结构基础8:二叉树oj+层序遍历。
二叉树oj+层序遍历
- 题目一:二叉树的销毁:
-
- 方法一:前序遍历:
- 方法二:后序遍历:
- 题目二:二叉树查找值为x的节点
-
- 方法一:
- 方法二:
- 方法三:
- 题目三:层序遍历:
-
- 方法一:
- 题目四:相同的树:
-
- 方法一:
- 题目五:对称二叉树:
-
- 方法一:
- 题目五:另一颗树的子树:
-
- 方法一:
- 题目六:二叉树的前序遍历:
-
- 方法一:
- 拓展:
- 题目七:翻转二叉树:
-
- 方法一:
- 题目八:判断是否为完全二叉树:
-
- 方法一:
- 题目九:二叉树遍历:
-
- 方法一:
题目一:二叉树的销毁:
方法一:前序遍历:
1.前序遍历需要先销毁根节点:
2.在销毁节点之前需要保存左右节点:
3.通过保存的节点的地址再一次进入函数进行递归:
4.总结:相当于从上向下遍历:
//2.销毁:
//方法一:(先序的销毁)保存根节点的左右节点的地址销毁自己。
void BeforeTreeDestory(struct TreeNode* root)
{
//1.根节点为空:
if (root == NULL)
return;
//2.保存左右节点的根节点:
struct TreeNode* left = root->left;
struct TreeNode* right = root->right;
free(root);
//3.进入递归:
BeforeTreeDestory(left);
BeforeTreeDestory(right);
}
方法二:后序遍历:
1.左子树右子树根,左子树又有左子树右子树根。
2.到走到返回的时候,这个时候左和右的走完回来了就可以销毁当前树的根
3.总结:这是一个先到最然后再去从下到上的销毁。
4.好处:不需要像前序遍历去保存左右节点的地址再一次进入递归(在返回的时候就可以销毁节点)
//方法二:(后序遍历)先进入左右子树然后这是一种从下到上的销毁:
void EndTreeDestory(struct TreeNode* root)
{
if (root = NULL)
return;
//进入左右子树回来才销毁:
EndTreeDestory(root->left);
EndTreeDestory(root->right);
//销毁根节点:
free(root);
}
题目二:二叉树查找值为x的节点
方法一:
1.使用先序遍历;
///
2.返回的条件:
1.根为空就返回说明没有找到:
2.找到值为x的节点返回节点的地址。
3.注意:数值不相同不需要返回说明还没有找到不需要返回:
3.返回的是节点的地址如果使用&& 和 || 逻辑运算符是不会返回地址的是只会返回0,1的这是需要注意的。
4.递归注意:因为我们需要返回节点的地址是需要从return一个节点之后从递归开辟的栈帧空间中带回来:
struct TreeNode* BinaryTreeFind(struct TreeNode* root, TreeNodeData x)
{
//1.根节点为空:
if (root == NULL)
return NULL;
//2.数值相同(找到值为X的节点不需要继续往下找了):
//只有数值相同的根节点才会被返回回来:
if (root->val == x)
return root;
//3.进入左右子树,这个数值到了非常深才可以被找到:
struct TreeNode* tmp1 = BinaryTreeFind(root->left, x);
if (tmp1 != NULL)
return tmp1;
struct TreeNode* tmp2 = BinaryTreeFind(root->right, x);
if (tmp2 != NULL)
return tmp2;
//左右子树都没有找到的情况:
return NULL;
}
方法二:
1.在方法一的基础上进行优化:
2.你会发现根据上面的两个判断:
1.如果根节点为空就返回NULL
2.如果数据相同就返回节点
3.如果这颗树没有数值相同的节点就返回NULL
总结:不需要对函数返回值进行判空处理直接让返回值作为判断条件是空就不会进入语句里面,如果不是空就一定是数值相等的节点的地址。返回地址就没有问题。
struct TreeNode* BinaryTreeFind(struct TreeNode* root, TreeNodeData x)
{
//1.根节点为空:
if (root == NULL)
return NULL;
//2.数值相同(找到值为X的节点不需要继续往下找了):
//只有数值相同的根节点才会被返回回来:
if (root->val == x)
return root;
//方法二:
struct TreeNode* tmp = NULL;
tmp = BinaryTreeFind(root->left, x);
if (tmp)
return tmp;
tmp = BinaryTreeFind(root->right, x);
if (tmp)
return tmp;
return NULL;
}
方法三:
1.如果左子树没有节点的话就直接返回右子树的函数返回值就可以:
2.右子树中无非只有两个情况:
1.有数据返回固定的节点地址:
2.找到底没有数据返回NULL
所以右子树的返回就不需要去判断:
struct TreeNode* BinaryTreeFind(struct TreeNode* root, TreeNodeData x)
{
//1.根节点为空:
if (root == NULL)
return NULL;
//2.数值相同(找到值为X的节点不需要继续往下找了):
//只有数值相同的根节点才会被返回回来:
if (root->val == x)
return root;
//方法三:
struct TreeNode* tmp = NULL;
tmp = BinaryTreeFind(root->left, x);
if (tmp)
return tmp;
return BinaryTreeFind(root->right, x);
//1.返回值需要接受,层层接受。
//2.防止返回值为空。
//3.或和与的运算符返回的值是0/1 地址丢失!
}
题目三:层序遍历:
方法一:
1.层序顾名思义就是一层一层的去遍历数据:
2.可以使用队列的数据结构保存数据:、
3.让根带左右子树
4.在根节点被pop之前top出节点并且访问数值去打印并且将左右子树的根节点入队列:
5.当队列为空说明二叉树的所有节点已经被层序遍历完全了:
//4.层序遍历: 队列存储:
void LevelOrder(struct TreeNode* root)
{
assert(root != NULL);
//初始化队列:
Que pQ;
QueueInit(&pQ);
//入根节点:
QueuePush(&pQ, root);
while (!QueueEmpty(&pQ))
{
//获取堆头的数据
QueueDatatype top = QueueFront(&pQ);
//打印队头数据:
if(top!=NULL)
printf("%d ", top->val);
//出去之前把孩子带进来(不需要递归的!!!)
if(top->left!=NULL)
QueuePush(&pQ, top->left);
if(top->right!=NULL)
QueuePush(&pQ, top->right);
//pop数据:
QueuePop(&pQ);
}
//销毁队列:
QueueDestor(&pQ);
}
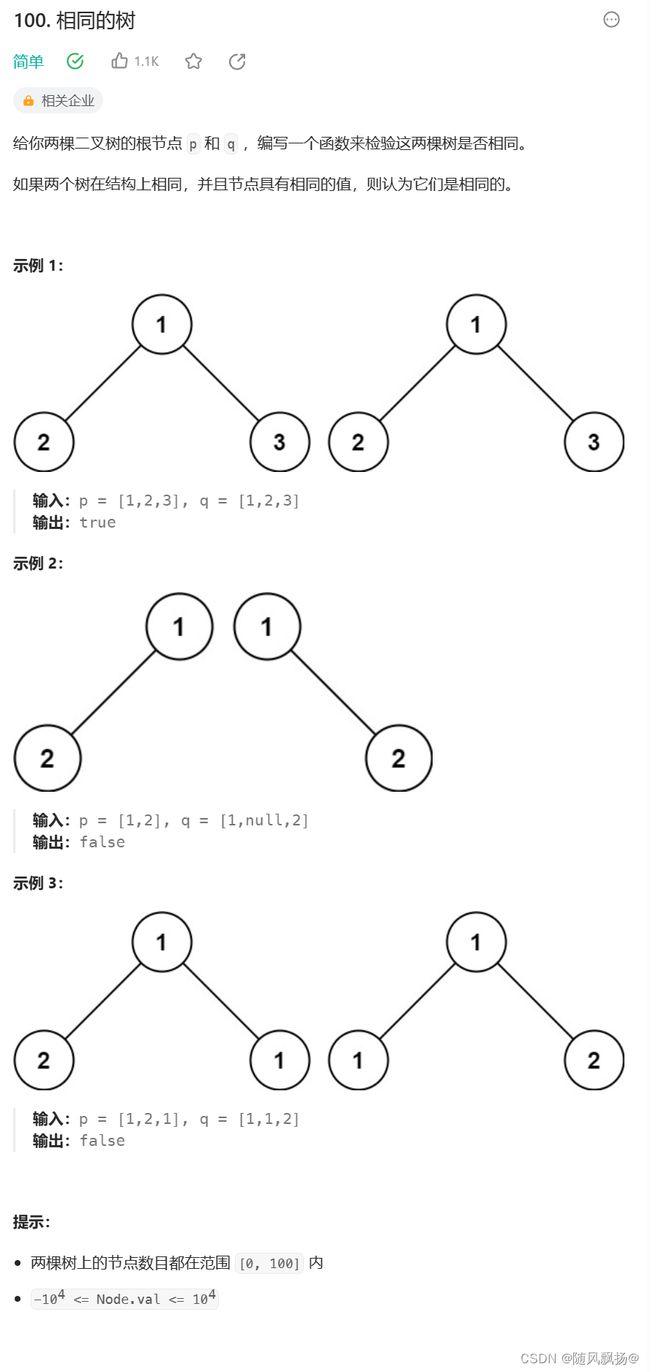
题目四:相同的树:
方法一:
bool isSameTree(struct TreeNode* p, struct TreeNode* q){
//1.如果两个都是空节点说明相同
if(p==NULL && q==NULL)
return true;
//2.经过1的判断p,q中至少有一个不是空是有数值的:
//这样的情况如果进入一定是false。
if(p==NULL || q==NULL)
return false;
//3.经过1,2的判断到这里一定满足两个节点都不是空节点。
//两个情况:
//1.两个节点的值不相同返回false
//2.两个节点的值相同但是还没有找完所有的节点所以继续进入递归寻找:
if(p->val != q->val)
return false;
//4.如果两个 左子树对应已经有不相同的了就不需要进入右树了:
return isSameTree(p->left,q->left)
&& isSameTree(p->right,q->right);
}
题目五:对称二叉树:
方法一:
1.这个题目和上面那个有一点点相似,这里比较一颗树的左右子树是否对称。上一个题目是比较直接给好的两个数的是否相同:
2.我们可以写一个子函数去传这一颗树的左右子树的根节点作为新的两颗树的根节点判断是否对称:
3.判断对称是判断相反的节点值是否相同(不同于判断俩颗树的相同相对位置的值是否相同)
bool isdouSymmetric(struct TreeNode* p ,struct TreeNode* q)
{
//两个都为空,走到底了!
if(p==NULL && q==NULL)
return true;
//一个空,一个不是空:
if(p==NULL || q==NULL)
return false;
//两个都不是空:L
if(p->val != q->val)
return false;
//第一个是判断左数的左和右树的右的对称:
//第二个是判断左数的右和右树的左的对称
return isdouSymmetric(p->left , q->right)
&&isdouSymmetric( p->right ,q->left );
}
bool isSymmetric(struct TreeNode* root){
//写一个子函数进入左右子树:
return isdouSymmetric(root->left,root->right);
}
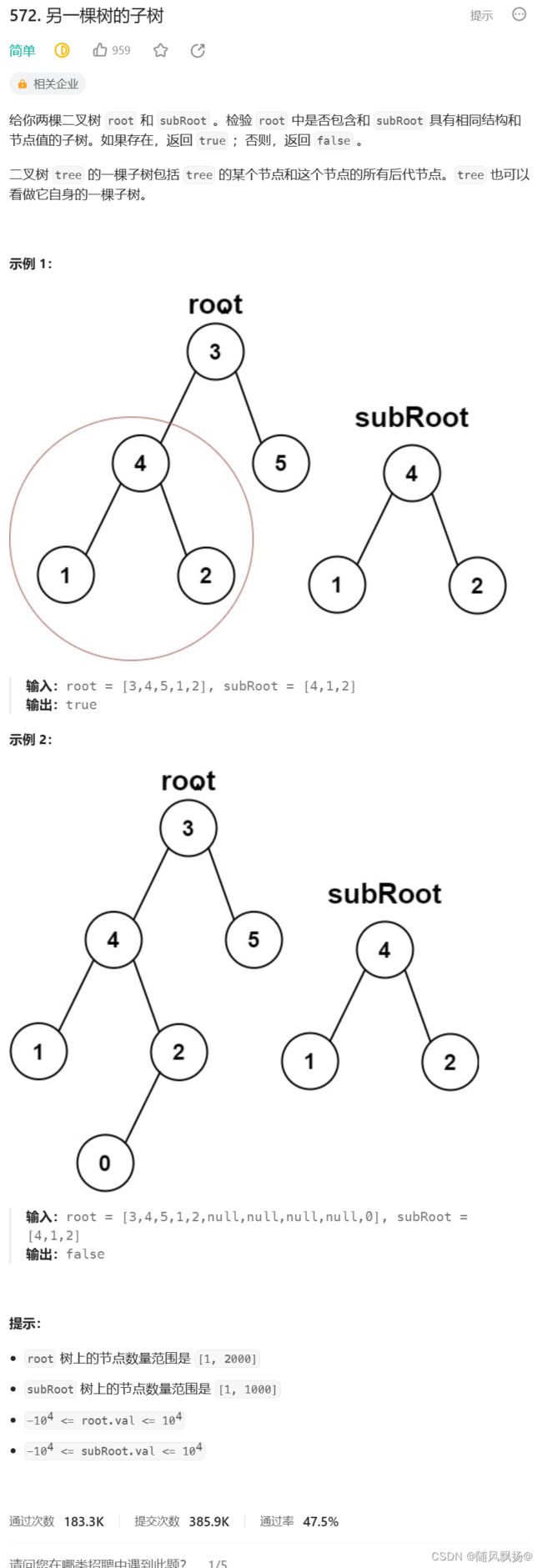
题目五:另一颗树的子树:
方法一:
1.有两个树一个树是父母。一颗树是儿子在父母中有可能找到儿子。
2.注意二子要和父母中的这个树完全相同直到后面都为空了不能说一部分相同后面还有一部分不相同的两个树:
3.我们前面写过判断两个数是否相同的函数现在找到父母这个数子树中的一个根和待比较树的根节点的相同就有可能存在相同的子树。
4.当父母这个数到空就说明这颗子树没有相同的树包括没有数值的相等:
5.原函数使用 || 连接的好处是如果左树中有相同的子树并且返回了true就不需要再加入右树去判断,如果左树中没有相同的树还可以到右树中去寻找。只有左右都为false才返回false表示不存在相同的子树!
bool isSameTree(struct TreeNode* p, struct TreeNode* q){
//1.两个空数
if(q==NULL && p==NULL)
{
return true;
}
//2.一个为空 另一个必须不为空:
if(p==NULL || q==NULL)
{
return false;
}
//3.两个数值一开始就不相等:
if(p->val != q->val)
{
return false;
}
return isSameTree(p->left,q->left)
&& isSameTree(p->right,q->right);
}
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){
//1.没有子树返回false
if(root==NULL)
return false;
//2.根节点的值相同有可能是相同子树的根节点:
if(root->val == subRoot->val)
{
if(isSameTree(root,subRoot))
{
return true;
}
}
//进入递归(先序遍历):
return isSubtree(root->left , subRoot)
|| isSubtree(root->right , subRoot);
}
题目六:二叉树的前序遍历:
方法一:
1.分析一下函数的参数和返回值:
1.返回一个数组的首地址(已经保存和前序遍历的数据)!
2.需要在堆区开辟空间这样才可以在外面找到这个数组的内容:
2.returnsize 返回数组的大小帮助外面去遍历数据:
3.使用计算节点个数的函数:
int TreeSize(struct TreeNode* root)
{
return root==NULL? 0: TreeSize(root->left)+TreeSize(root->right)+1;
}
void Traversal(struct TreeNode* root , int* tmp , int* i)
{
if(root==NULL)
return;
tmp[*i]=root->val;
(*i)++;
Traversal(root->left , tmp , i);
Traversal(root->right, tmp , i);
}
int* preorderTraversal(struct TreeNode* root, int* returnSize){
//1.开辟数组,返回顺序表长度
int n=TreeSize(root);
*returnSize = n;
int* tmp=(int*)malloc(sizeof(int)*n);
//2.给顺序表中添加内容:
int i=0;
Traversal(root , tmp , &i);
return tmp;
}
拓展:
中序遍历:题目链接
后序遍历:题目链接
题目七:翻转二叉树:
方法一:
1.不需要考虑左右子树为空的情况.
2.直接进行交换,下一次递归进入函数如果为空就会返回用了下一次函数判断当前为空的处理!
3.翻转是翻转每一颗树左右子树的根节点的情况!
void convert(struct TreeNode* root)
{
if(root==NULL)
return;
struct TreeNode* tmp=NULL;
tmp=root->left;
root->left=root->right;
root->right=tmp;
convert(root->left);
convert(root->right);
}
struct TreeNode* invertTree(struct TreeNode* root){
if(root==NULL)
return root;
convert(root);
return root;
}
题目八:判断是否为完全二叉树:
方法一:
1.判断完全二叉树我们需要使用到层序遍历的方法:
2.完全二叉树的特点是:前面k-1层有序k层从左到右连续是没有空出现的。
3.当一个节点从队列中出去的时候就把这个节点的左右孩子入队列。
4.根据完全二叉树的特点第一次遍历到空就跳出去,继续进行获取队头数据判断是空还是节点,有一个节点就说明这不是一个完全二叉树:
//1.判断是否为完全二叉树:
int BinaryTreeComplete(struct TreeNode* root)
{
assert(root != NULL);
Que TQ;
QueueInit(&TQ);
//1.入队列:
QueuePush(&TQ, root);
while (!QueueEmpty(&TQ))
{
//2.获取队头数据:
QueueDatatype top = QueueFront(&TQ);
//3.带入左右孩子:
if (top != NULL)
{
QueuePush(&TQ, top->left);
QueuePush(&TQ, top->right);
}
QueuePop(&TQ);
//4.遇到了我们第一个空:
if (top == NULL)
{
break;
}
}
while (!QueueEmpty(&TQ))
{
//2.获取队头数据:
QueueDatatype top = QueueFront(&TQ);
//3.带入左右孩子:
if (top != NULL)
{
QueuePush(&TQ, top->left);
QueuePush(&TQ, top->right);
}
QueuePop(&TQ);
//4.如果遇到了我们第一个不是空:
if (top != NULL)
{
return false;
}
}
QueueDestor(&TQ);
return true;
}
int main()
{
struct TreeNode* n1 = byNode(1);
struct TreeNode* n2 = byNode(2);
struct TreeNode* n3 = byNode(3);
struct TreeNode* n4 = byNode(4);
struct TreeNode* n5 = byNode(5);
struct TreeNode* n6 = byNode(6);
n1->left = n2;
n1->right = n3;
n2->left = n4;
n2->right = n5;
//n3->right = n6;
//n3->left = n6;
if (BinaryTreeComplete(n1))
{
printf("是一个完全二叉树\n");
}
else
{
printf("不是完全二叉树\n");
}
return 0;
}
题目九:二叉树遍历:
二叉树遍历:题目链接
方法一:
1.递归遍历字符串。两个情况:
1.字符不是# ,2.字符是#返回空说明这一路的递归结束需要返回连接:
2.递归的过程中需要去++i控制我们的递归函数的一个全局变量!
3.每一次返回空或者构建好节点放好符号之后就(*i)++ 控制每一次访问到的字符。
4。总结:构建二叉树是在返回过程中进行连接的,在进入过程中进行创建节点和赋值数据的。
#include