数据结构队列的基本操作
栈和队列
栈和队列是两种重要的线性结构。从数据结构角度看,栈和队列也是线性表,其特殊性在于栈和队列的基本操作是线性表操作的子集,他们是操作受限的线性表,因此,可称为具有限定性的数据结构,但从数据类型角度看,他们是和线性表不相同的两类重要的抽象数据类型。
一、栈和队列的定义和特点
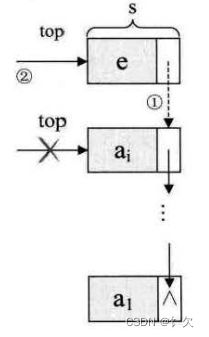
栈是限定仅在表尾进行插入或删除操作的线性表。表尾端称为栈顶,表头端称为栈底,不含元素的空表称为空栈。
假设栈S=(a1,a2,…an),则称a1为栈底元素,an为栈顶元素。退栈的第一个元素应为栈顶元素。栈的修改是按后进先出的原则进行的,因此,栈又称为后进先出的线性表。
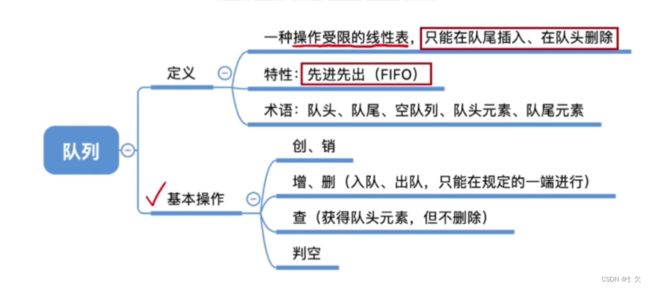
队列是一种先进先出的线性表,它只允许在表的一端进行插入,而在另一端删除元素。允许插入的一端为队尾,允许删除的一端为队头。
二、栈的表示和操作的实现
基本操作
- InitStack(&S) 构造一个空栈S
- Destroy(&S) 销毁栈S
- ClearStack(&S) 将栈S清空
- StackEmpty(S) 若空栈为true,否则false
- StackLength(S) 返回S的元素个数
- GetTop(S) 返回S的栈顶元素,不修改栈顶指针
- Push(&S,e) 插入元素e为新的栈顶元素
- Pop(&S,&e) 删除S的栈顶元素,并用e返回其值
- StackTraverse(S) 从栈底到栈顶依次对S的每个数据元素进行访问
1.顺序栈的表示和实现
代码如下(示例):
//--------------顺序栈的存储结构--------------------
#define MAXSIZE 100
typedef struct
{
SElemType *base; //栈底指针
SElemType *top; //栈顶指针
int stacksize; //栈可用的最大容量
}SqStack;
1.初始化
Status InitStack(SqStack &S)
{
S.base=mew SElemType[MAXSIZE]; //为顺序栈动态分配一个最大容量为MAXSIZE的数组空间
if(!S.base) return ERROR; //存储分配失败
S.top=S.base; //top初始化为base,空栈
S.stacksize==MAXSIZE; //stacksize置为栈的最大容量MAXSIZE
return OK;
}
2.入栈
Status Push(SqStack &S,SElemType e)
{
if(S.top-S.base==S.stacksize) return ERROR; //栈满
*S.top++=e; //将元素e压入栈顶,栈顶指针加1
return OK;
}
3.出栈
Status Pop(SqStack &S,SElemType &e)
{
if(S.top==S.base) return ERROR; //栈空
e=*--S.top; //栈顶指针减1,将栈顶元素赋给e
return OK;
}
4.取栈顶元素
SElemType GetTop(SqStack S)
{
if(S.top!=S.base)
return *(S.top-1);
}
2.链栈的表示和实现
代码如下(示例):
//---------链栈的存储结构-----------------
typedef struct StackNode
{
ElemType data;
struct StackNode *next;
}StackNode,*LinkStack;
1.初始化
链栈的初始化操作就是设置一个空栈,因为没必要设置头结点,所以直接把栈顶指针置空即可。
Status InitStack(LinkStack &S)
{
S=NULL;
return OK;
}
2.入栈
和顺序栈的入栈操作不同是它不需要入栈前判断是否栈满,只需要分配为入栈元素动态分配一个节点空间即可。
Status Push(LinkStack &S,SElemType e)
{
p=new StackNode;
P->data=e;
p->next=S; //将新节点插入栈顶
S=p; //修改栈顶指针p
return OK;
}
3.出栈
和顺序栈的一样,链栈在出栈前也需要判断栈是否为空,不同的是,链栈在出栈后需要释放出栈元素的栈顶空间。
1 判断栈空
2 栈顶元素赋给e
3 临时保存栈顶空间
4 修改栈顶指针,指向新的栈顶元素
5 释放原栈顶元素的空间
Status Pop(LinkStack &S,SElemType &e)
{
if(S==NULL) return ERROR;
e=S->data;
p=S;
S=S->next;
delete p;
return OK;
}
4.取栈顶元素
栈顶指针保持不变。
SElemType GetTop(LinkStack S)
{
if(S!=NULL)
return S->data;
}
5.输出栈
给定一个初始为空的栈和一系列进栈、出栈操作,请编写程序输出经过这些操作后栈的元素。栈的元素值均为整数。
输入格式:
输入第1行为1个正整数n,表示操作个数;
第2行为给出的n个整数,非0元素表示进栈,此非0元素即为进栈元素,0元素表示出栈。
保证栈中元素个数不超过10个。
输出格式:
第一行按出栈顺序输出所有出栈元素,以一个空格隔开;如果栈满时做进栈操作会输出"FULL”,如果栈空时做出栈操作会输出"EMPTY";
第二行中输出栈中所有元素,以一个空格隔开。
末尾均有一个空格。
输入样例:
12
3 1 2 0 0 -1 0 0 0 4 5 0
输出样例:
2 1 -1 3 EMPTY 5
4
#include 判断选择
- 采用顺序存储结构的循环队列,出队操作会引起其余元素的移动。 F
- 顺序栈中元素值的大小是有序的。 F
- 在n个元素连续进栈以后,它们的出栈顺序和进栈顺序一定正好相反。 F
- 栈是一种对进栈、出栈操作总次数做了限制的线性表 F
- 对顺序栈进行进栈、出栈操作不涉及元素的前、后移动问题。 T
- 栈结构不会出现溢出现象。 F
- (neuDS)在顺序栈中,若栈顶指针top指向栈顶元素的下一个存储单元,且顺序栈的最大容量是maxSize,则顺序栈的判空条件是( A)。//指向下一个的是0 指向栈顶位置是-1
A.top==0B.
B.top==-1
C.top==maxSize
D.top==maxSize-1
注:顺序栈是数组;另一种栈顶指针:将top指向栈顶元素的存储位置,空栈时top=-1
- neuDS)在顺序栈中,若栈顶指针top指向栈顶元素的下一个存储单元,且顺序栈的最大容量是maxSize。则顺序栈的判满的条件是( C )。
A.
top==0
B.
top==-1
C.
top==maxSize
D.
top==maxSize-1
- 借助堆栈将中缀表达式A-(B-C/D)*E转换为后缀表达式,则该堆栈的大小至少为:C
A.
2
B.
3
C.
4
D.
5
栈是(C )。
A.
顺序存储的线性结构
B.
链式存储的非线性结构
C.
限制存取点的线性结构
D.
限制存储点的非线性结构
- 设有一个顺序共享栈Share[0:n-1],其中第一个栈顶指针top1的初值为-1,第二个栈顶指针top2的初值为n,则判断共享栈满的条件是(A )。
A.
top2-top1==1
B.
top1-top2==1
C.
top1==top2
D.
以上都不对
- 栈的应用不包括( D)。
A.
递归
B.
进制转换
C.
迷宫求解
D.
缓冲区
- 判定一个顺序栈st(最多元素为MaxSize)为空的条件是(B)。
A.
st->top != -1
B.
st->top == -1
C.
st->top != MaxSize
D.
st->top == MaxSize
- 下列算法的功能是(B)。
void func( )
{
int x;
Statck s; //定义栈s
cin >> x;
while (x<>0)
{
push(s,x);
cin>>x;
}
while (!EmptyStack(s))
cout << pop(s);
}
A.
以读入数据的相同顺序输出数据
B.
以读入数据的相反顺序输出数据
C.
将数据读入到栈中进行保存
D.
读入一批数据到栈中进行求和并输出
(B)中任何两个结点之间都没有逻辑关系。
A.
树形结构
B.
集合
C.
图形结构
D.
线性结构
一个递归算法必须包括(B )。
A.
递归部分
B.
终止条件和递归部分
C.
迭代部分
D.
终止条件和迭代部分
- 对算法分析的前提是( B)。
A.
算法必须简单
B.
算法必须正确
C.
算法结构性强
D.
算法必须通用
- 对于线性表,在顺序存储结构和链式存储结构中查找第k个元素,其时间复杂性分别是多少? D
A.
都是O(1)
B.
都是O(k)
C.
O(k)和O(1)
D.
O(1)和O(k)
- 将两个各有n个元素的递增有序顺序表归并成一个有序顺序表,其最少的比较次数是( A)
A.
n
B.
2n-1
C.
2n
D.
n-1
//因为已经递增有序了 不需要n次比较顺序
已知指针p和q分别指向某单链表中第一个结点和最后一个结点。假设指针s指向
另一个单链表中某个结点,则在s所指结点之后插入上述链表应执行的语句为(A )
A.
q->next=s->next;s->next=p;
B.
s->next=p;q->next=s->next;
C.
p->next=s->next;s->next=q;
D.
s->next=q;p->next=s->next
在一个长度为n(n>1)的带头节点的单链表head上,另设有尾指针r(指向尾节点),执行 ( B) 操作与链表的长度有关
//从头遍历
A.
删除单链表中的第一个元素
B.
删除单链表中的尾节点
C.
在单链表第一个元素前插入一个新节点
D.
在单链表最后一个元素后插入一个新节点
在双向链表中,前驱指针为prior,后继指针为next,在p指针所指的结点后插入q所指向的新结点,其语句序列是( B)
A.
q->prior=p; q->next=p->next; p->next=q; p->next->prior=q;
B.
q->prior=p; q->next=p->next; p->next->prior=q; p->next=q;
C.
p->next=q; p->next->prior=q; q->prior=p; q->next=p->next;
D.
p->next=q; q->prior=p; p->next->prior=q; q->next=q;
假设栈初始为空,将中缀表达式a/b+(c*d-e*f)/g转换为等价的后缀表达式的过程中,当扫描到f时,栈中的元素依次是(B)。
栈 表达式
/ ab
+ ab/
+(* ab/cd
+(-* ab/cd* //当遇到)
+(-* ab/cd*ef
+ ab/cd*ef*-
+/ ab/cd*ef*-g
^ ab/cd*ef*-g/+
A.
+(*-
B.
+(-*
C.
/+(*-*
D.
/+-*
- 在作进栈运算时,应先判别栈是否(① );在作退栈运算时应先判别栈是否(② )。当栈中元素为n个,作进栈运算时发生上溢,则说明该栈的最大容量为(③ )。**B**
①: A. 空 B. 满 C. 上溢 D. 下溢
②: A. 空 B. 满 C. 上溢 D. 下溢
③: A. n-1 B. n C. n+1 D. n/2
A.
① C ② D ③ B
B.
① B ② A ③ B
C.
① B ② B ③ A
D.
① B ② A ③ A
4.若一个栈元素用数组data[1..n]存储,初始栈顶指针top为n,则以下元素x进栈最适合的操作是______。
A、top++; data[top]=x;
B、data[top]=x; top++;
C、top--; data[top]=x;
D、data[top]=x; top--;
答案:['data[top]=x; top--;']
5.若一个栈元素用数组data[1..n]存储,初始栈顶指针top为n,则以下出栈元素x最适合的操作是______。
A、x=data[top]; top++;
B、top++; x=data[top];
C、x=data[top]=x; top--;
D、top--; x=data[top];
答案:['top++; x=data[top];']
6.若一个栈元素用数组data[1..n]存储,初始栈顶指针top为0,则以下元素x进栈最适合的操作是______。
A、top++; data[top]=x;
B、data[top]=x; top++;
C、top--; data[top]=x;
D、data[top]=x; top--;
答案:['top++; data[top]=x;']
7.若一个栈元素用数组data[1..n]存储,初始栈顶指针top为0,则以下出栈元素x最适合的操作是______。
A、x=data[top]; top--;
B、x=data[top]; top++;
C、top--; x=data[top];
D、top++; x=data[top];;
答案:['x=data[top]; top--;']
若一个栈元素用数组data[1..n]存储
> 初始栈顶指针为0
> 入栈 先加后压
> 出栈 先弹后减
>
> 初始栈顶指针为n 指针往下面走 指向数据块下面
> 入栈 先压后减 (c++top指向base时候 其实是先压后加)
> 出栈 先加后弹(c++top指向base时候 其实是先减后弹)
> 初始栈顶指针为1
> 入栈 符合先加后压的原则 但是指针是1 有位置 所以可以先进来再加第二个指针 变成了先压后加
> 出栈 可以先减后弹 因为有位置
- 若一个栈用数组data[1..n]存储,初始栈顶指针top为1,则以下元素x进栈的正确操作是(B )
A.
top++; data[top]=x;
B.
data[top]=x; top++;
C.
top--; data[top]=x;
D.
data[top]=x; top--;
设栈S和队列Q的初始状态为空,元素e1、e2、e3、e4、e5和e6依次通过S,每个元素出栈后即进入Q,若6个元素出队的序列是e2、e3、e5、e4、e6和e1,则栈S的容量至少应该是( B)
e 1 2
1 23
145 2354
16 2354
^ 235461
> //
A.
2
B.
3
C.
4
D.
5
- 某堆栈采用顺序存储的方式,存储在数组data[0..n]中。栈顶指示器是top (top指向实际栈顶元素)。在栈非满的情况下,值为x的元素入栈的操作用***C语言***表示为( B)。
//C语言是先加指针后压入
A.
data[top++]=x;
B.
data[++top]=x;
C.
data[top--]=x;
D.
data[--top]=x;
- 循环队列的引入,目的是为了克服(A )。
A.
假溢出问题
B.
真溢出问题
C.
空间不够用
D.
操作不方便
对单链表来说,只有从头结点开始才能访问到表中所有结点。T
```cpp
1. 栈和队列具有相同的(逻辑结构)
2. 栈是(限制存取点的线性结构)
3. 设栈表不带头结点且所有操作均在表头进行,则下列最不适合作为链栈的是(C)
A 只有表头结点指针,没有表尾指针的双向循环链表。
B 只有表尾指针,没有表头指针的双向循环链表
C 只有表头结点指针,没有表尾指针的单向循环链表
D 只有表尾指针,没有表头指针的单向循环链表
> 对于双向循环链表,不管是表头指针还是表尾指针,都可以很方便地找到表头结点,方便在表头做插入和删除操作,而单循环链表通过尾指针可以很方便地找到表头结点,**但通过头指针找尾结点需要遍历一次链表。**
4. 三个不同元素依次进栈,能得到(5)种不同的出栈序列。 1/(n+1)C{n,2n}
5. 若一个栈的输入序列是1,2,3,...n,输出序列的第一个元素是n,则第i个输出元素为(n-i+1) 第n个元素第一个出栈 说明前面n-1个出去了,按照先进后出原则,第i个则是n-(i-1)
6. 一个栈的输入序列是1,2,3,...n,输出序列的第一个元素是i,则第j个元素是(不确定) i之前的元素可以排在i后面依次出栈,但是i后面的元素可以进栈也可以排在i之前的元素出栈。
7. 某栈的输入序列为a,b,c,d,下面四个序列中,不可能为其输出序列的是(d,c,a,b)
8. 若一个栈的输入序列是P1,P2,...,Pn,输出序列是1,2,3,...n,若P3=1,则P1的值是(不可能是2)
[入栈序列是P1,P2,P3,...,Pn,由于P3=1,即P1,P2,P3连续入栈后,第一个出栈元素是P3,说明P1,P2已经按序进栈,根据先进后出的特点,P2必定在P1前面出栈,而第二个出栈元素是2,则P1的值不可能是2]
9. 已知一个栈的入栈序列是1,2,3,4,其出栈序列为P1,P2,P3,P4,则P2,P4不可能是(4,3)
- [当4在栈中时,意味着123都入栈或在栈中,如果4第二个出栈,则为P2,则P3,P4只有(1,2),(1,3),(2,3)三种可能,如果是(1,2),则P1一定为3,3则不能在P4位置出现;如果是(1,3)(2,3),下一个出栈元素必定是3,则P3一定是3 所以P2不能是4,P4也不能是3 ]
10.采用共享栈的好处是(节省存储空间,降低发生上溢的可能)
11.【2009统考真题】设栈S和队列Q的初始状态均为空,元素abcdefg依次进入栈S。若每个元素出栈后立即进入队列Q,且7个元素出队的顺序是bdcfeag,则栈S的容量至少是(3)
10. **【2013统考真题】一个栈的入栈序列为1,2,3,...n,出栈序列为P1,P2,...Pn。若P2=3,则P3可能取值的个数是(n-1)**
- [3之后的456...n都可能为P3(持续入栈直到该数入栈后立即出栈)。接下来分析1和2,P1可以是3之前入栈的数(1或2),**也可能是4:** 当P1为1时,P3可以取2;当P1=2时,P3可以取1;当P1=4时,P3可以取134之外的所有数,所以P3可能取值的个数为n-1]
队列的表示和操作的实现
1.队列的顺序表示和实现
//-------队列的顺序存储结构-----------------
#include 1.初始化
算法步骤:
① 为队列分配一个最大容量为MAXQSIZE的数组空间 ,base指向数组空间的首地址。
② 将头指针和尾指针置为0,表示队列为空。
Status InitQueue(SqQueue &Q)
{
Q.base=new QElemType[MAXQSIZE];
if(!Q.base) return ERROR;
Q.front=Q.rear=0;
return OK;
}
2.队列长度
Statue QueueLength(SqQueue &Q)
{
return (Q.rear-Q.front+MAXQSIZE)%MAXQSIZE;
}
3.入队
Status EnQueue(SqQueue &Q,QElemType e)
{
if((Q.rear+1)&MAXQSIZE==Q.front) //若尾指针加1后等于头指针则队满
return ERROR;
Q.base[Q.rear]=e;
Q.rear=(Q.rear+1)%MAXQSIZE;
return OK;
}
4.出队
Status DeQueue(SqQueue &Q,QElemType &e){
if(Q.front==Q.rear) return ERROR; //队空
e=Q.base[Q.front];
Q.front=(Q.front+1)%MAXQSIZE;
return OK;
}
5.取队头元素
QElemType GetHead(SqQueue &Q)
{
if(Q.front!=Q.rear) //队列非空
return Q.base[Q.front]; //返回队头元素的值,队头指针不变。
}
1.链队列----队列的链式表示和实现
//----------队列的链式存储结构-------
typedef struct QNode{
QElemType data;
struct QNode *next; //指针域
}QNode,*QueuePtr;
typedef struct{
QueuePtr front;
QueuePtr rear;
}LinkQueue;
Status InitQueue(LinkQueue &Q)
{//构造一个空队列
Q.front=Q.rear=new QNode; //生成一个新的节点作为头节点,队头和队尾指向此节点
Q.front->next=NULL; //头节点的指针域置空
return OK;
}
2.入队
Status EnQueue(LinkQueue &Q,QElemType e)
{
p=new QNode;
p->data=e;
p->next=NULL;
Q.rear->next=p;
Q.rear=p;
return OK;
}
3.出队
Status DeQueue(LinkQueue &Q,QElemType &e)
{
if(Q.front==Q.rear) return ERROR;
p=Q.front->next; //p指向队头元素
e=p->data; //e保存队头元素的值
Q.front->next=p->next;
if(Q.rear==p) Q.rear=Q.front; //最后一个元素被删,队尾指向队头
delete p;
return OK;
}
5.取队头元素
QElemType GetHead(LinkQueue Q)
{
if(Q.front!=Q.rear)
return Q.front->next->data;//返回头节点的值,队友指针不变。
}
Status ClearQueue(LinkQueue &Q){
QueuePtr p,q;
Q->rear =Q->front;//跟初始状态相同,Q->rear指向头结点
p=Q->front->next;//开始销毁队头元素,队头,队尾依然保留
Q->front->next =NULL;
while(p){
q=p;
p=p->next;
free(q);
}
return OK;
}
Status DestroyQueue(LinkQueue &Q){
while(Q->front){
Q->rear=Q->front->next;//从队头开始销毁
free(Q->front);
Q->front = Q->rear;
}
return OK;
}
Status visit(QElemType e)
{
printf("%d ",e);
return OK;
Status QueueTraverse(LinkQueue Q){
QueuePtr p;
p=Q.front->next;
while(p){
visit(p->data);
p=p->next;
}
printf("\n");
return OK;
}
int main(){
int i;
QElemType d;
LinkQueue q;
i=InitQueue(q);
//入队
for(int index=0;index<MAXQSIZE;index++){
EnQueue(q,index);
}
QueueTraverse(q);
DestroyQueue(q);
printf("队列已经销毁,q.front=%p q.rear=%p\n",q.front, q.rear);
return 0;
}
在一个链表表示的队列中, f和r分别指向队列的头和尾。下列哪个操作能正确地将s结点插入到队列中:
B
A.
f->next=s; f=s;
B.
r->next=s; r=s;
C.
s->next=r; r=s;
D.
s->next=f; f=s;
若用数组A[0...5]来实现循环队列,且当前rear和front的值分别为1和5,当从队列中删除一个元素,再加入两个元素后,rear和front的值分别为( )。
> rear : (1+2)%6=3
> front :(5+1)%6=0
A.
3和4
B.
3和0
C.
5和0
D.
5和1
循环队列放在一维数组A[0...M-1]中,end1指向队头元素,end2指向队尾元素的后一个位置。假设队列两端均可进行入队和出队操作,队列中最多能容纳M-1个元素。初始时为空。下列判断队空和队满的条件中,正确的是(A )。
A.
队空:end1==end2;队满:end1==(end2+1)mod M
B.
队空:end1==end2;队满:end2==(end1+1)mod (M-1)
C.
队空:end2==(end1+1) mod M;队满:end1==(end2+1) mod M
D.
队空:end1==(end2+1) mod M;队满:end2==(end1+1)mod (M-1)
最不适合用作链队的链表是(A)。
> 起码是个环 要能循环
A.
只带队头指针的非循环双链表
B.
只带队头指针的循环双链表
C.
只带队尾指针的循环双链表
D.
只带队尾指针的循环单链表
选C
> 先入先出原则 驶出顺序1-9
> 8 9
> 4 5 6 7
> 2 3
>1
A.
2
B.
3
C.
4
D.
5
循环队列___C_。
A.
不会产生溢出
B.
不会产生上溢出
C.
不会产生假溢出
D.
以上都不对
现采用大小为10的数组实现一个循环队列。设在某一时刻,队列为空且此时front和rear值均为5。经过若干操作后,front为8,rear为2,问:此时队列中有多少个元素?
A
> (2-8+10)%10=4
A.
4
B.
5
C.
6
D.
7
已知循环队列的结构定义如下:
typedef struct
{
int size, front, rear;
int *element;
} AQUEUE;
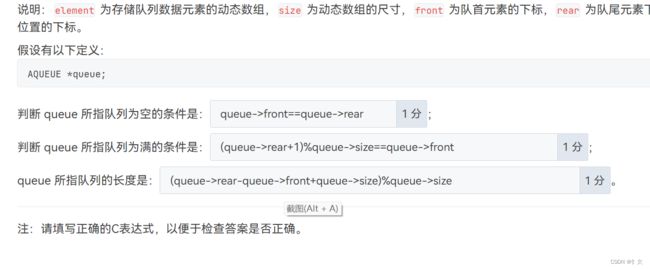
说明:element 为存储队列数据元素的动态数组,size 为动态数组的尺寸,front 为队首元素的下标,rear 为队尾元素下一位置的下标。
本题要求实现一个普通顺序队列。
当输入1 2 3 -1时,输出为1 2 3 。
当输入为1 2 3 4 5 6 7 8 9 10 11 -1时,输出为
queue is full!
1 2 3 4 5 6 7 8 9 10
请填空。
#include 给定一个初始为空的队列和一系列入队、出队操作,请编写程序输出每次出队的元素。队列的元素值均为整数。
输入格式:
输入第1行为1个正整数n,表示操作个数;接下来n行,每行表示一个操作,格式为1 d或0。1 d表示将整数d入队,0表示出队。n不超过20000。
输出格式:
按顺序输出每次出队的元素,每个元素一行。若某出队操作不合法(如在队列空时出队),则对该操作输出invalid。
输入样例:
7
1 1
1 2
0
0
0
1 3
0
输出样例:
1
2
invalid
3
#include 假设男士和女士的记录存放在一个数组中,设计算法实现舞伴配对,要求输出配对的舞伴,并输出没有配对的队头元素的姓名。
函数接口定义:
void DancePartner(DataType dancer[], int num) ;
其中 dancer[]是存放男士和女士信息的数组,num是数组大小。
裁判测试程序样例:
#include约瑟夫问题:有n只猴子,按顺时针方向围成一圈选大王(编号从1到n),从第1号开始报数,一直数到m,数到m的猴子退出圈外,剩下的猴子再接着从1开始报数。就这样,直到圈内只剩下一只猴子时,这个猴子就是猴王,编程求输入n,m后,输出最后猴王的编号。
输入格式:
每行是用空格分开的两个整数,第一个是 n, 第二个是 m ( 0 < m,n <=300)。最后一行是:
0 0
输出格式:
对于每行输入数据(最后一行除外),输出数据也是一行,即最后猴王的编号
输入样例:
6 2
12 4
8 3
0 0
输出样例:
5
1
7
#include 用链队列作存储结构,实现队列(元素为整型)的基本运算。
链队列的类型定义:
typedef int ElemType;
typedef struct QNode
{
ElemType data;
struct QNode *next;
}QNode;
typedef struct
{
QNode *front;
QNode *rear;
}LinkQueue;
输入格式:
在一行输入若干个队列元素值,调用入队函数把输入的元素值入队,用−1表示输入结束(−1不属于队列)。
输出格式:
输出分两行:
第一行输出队头元素。如队列为空,输出NULL。
第二行依次输出出队元素,直到队列为空。元素间以空格分隔,队列为空时输出NULL。
输入样例:
1 3 5 7 9 -1
输出样例:
Head:1
Pop:1 3 5 7 9 NULL
输入样例:
-1
输出样例:
Head:NULL
Pop:NULL
#include