JLU数据结构上机实验1

7-1 重复计数

原题呈现：

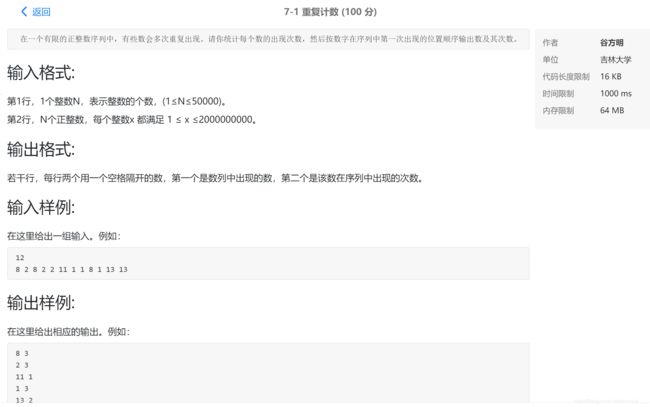
解题思路 ：这道题数据可能比较水 这道题可以用暴力法求解。开一个二维数组a[50001][2]，每一行的第一个数保存数列中的数，第二个数保存该数在数列中出现的次数。遍历数列，每读入一个数，遍历数组判断该数是否已经在数组中。如果是，出现次数+1；如果否，将该数保存在数组中并将出现次数初始化为1.

以下是根据这一思路写出的代码：

#include 
#include 
#include 

int main() {
	long long a[50001][2],temp;
	int n, i, j, count = 0,flag=0;
	scanf("%d", &n);
	for (i = 0; i < n; i++)
		a[i][1] = 0;
	for (i = 0; i < n; i++) {
		scanf("%lld", &temp);
		if (i == 0) {
			a[0][0] = temp;
			a[0][1] = 1;
			count = 1;
			continue;
		}
		for (j = 0; j < count; j++) {
			if (a[j][0] == temp) {
				a[j][1]++;
				flag = 1;
				break;
			}
		}
		if (!flag) {
			count++;
			a[count-1][0] = temp;
			a[count-1][1]++;
		}
		flag = 0;
	}
	for (i = 0; i < count; i++) {
		printf("%lld %lld\n", a[i][0], a[i][1]);
	}

	return 0;
}

解后反思：这道题数据真的比较水 以上方法时间复杂度是O（n^2)级别的，不尽如人意。可以考虑改进对一个数是否已经出现过的判断，一个可以采用的方法是利用STL中的set容器；另外，学习过炫神的博客后，我也发现了可以利用sort排序结合lower_bound，upper_bound很方便地求解这个问题。

7-2 报数游戏

原题呈现：

解题思路 ： 这是一个典型的约瑟夫环问题，可以用循环链表解决。

以下是根据这一思路写出的代码：

#include 
#include 
#include 

typedef struct x {
	int num;
	struct x* next;
}xtype;
typedef xtype* pxtype;
pxtype head, rear, q, q0;

int main() {
	int n, m, i, count = 0;
	scanf("%d %d", &n, &m);

	for (i = 0; i < n; i++) {
		pxtype p;
		p = (pxtype)malloc(sizeof(xtype));
		p->num = i + 1;
		if (i == 0) {
			head = p;
			rear = p;
			p->next = head;
		}
		else {
			rear->next = p;
			rear = p;
			p->next = head;
		}
	}
	q0 = head;
	q = head;
	if (m == 1) {
		while (count < n) {
			printf("%d", q->num);
		    if (count != n - 1)
			    printf(" ");
			q = q->next;
			count++;
		}
		return 0;
	}
	while (count < n) {
		for (i = 1; i < m; i++) {
			q0 = q;
			q = q->next;
		}
		printf("%d", q->num);
		if (count != n - 1)
			printf(" ");
		q0->next = q->next;
		free(q);
		count++;
		q = q0->next;
	}

	return 0;
}

解后反思： 虽然循环链表能够解决这个问题，但是略显繁琐，可以用静态链表达到相同的效果。

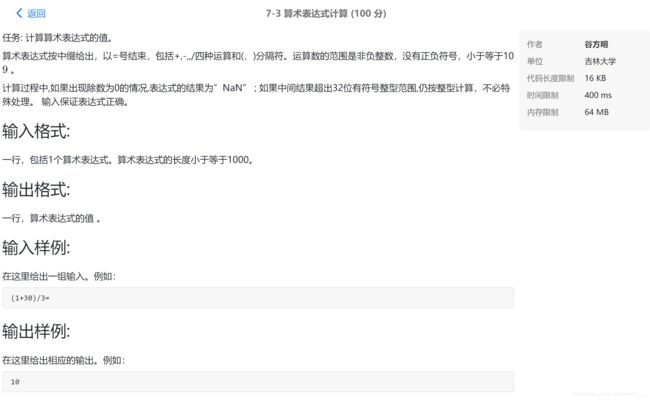
7-3 算术表达式计算

原题呈现：

解题思路 ： 开两个栈：一个数字栈保存数字，一个符号栈保存运算符。如果读入的是一个数字，直接入栈；如果读入的是运算符，如果栈空那么直接入栈，否则首先将其与符号栈顶的运算符优先级比较，如果栈顶的优先级大于等于当前运算符，那么需要先把栈顶的运算符计算掉。一直重复下去，直到栈空或者遇到栈顶的优先级比当前运算符的优先级低，这时当前运算符才能入栈。如果遇到了左括号，直接入栈；如果遇到了右括号，那么就把之前栈中的左括号和当前右括号中间夹着的运算符全部运算掉，同时把左括号出栈，右括号不用入栈。在表达式合法的前提下，最后数字栈的栈顶元素就是表达式的值。

以下是根据这一思路写出的代码：

#include 
#include 
#include 

int main(){
	char str[10000],ch;
	int len,s1[10000],s2[10000],top1=-1,top2=-1,i=0,temp=0;
	scanf("%s",str);
	len=strlen(str);
	while(1){
		if(str[i]=='='){
			while(top2!=-1){
				temp=0;
				if(s2[top2]=='+'){
					temp=s1[top1-1]+s1[top1];
					top1-=2;
					s1[++top1]=temp;
					top2--;
				}
				else if(s2[top2]=='-'){
					temp=s1[top1-1]-s1[top1];
					top1-=2;
					s1[++top1]=temp;
					top2--;
				}
				else if(s2[top2]=='*'){
					temp=s1[top1-1]*s1[top1];
					top1-=2;
					s1[++top1]=temp;
					top2--;
				}
				else if(s2[top2]=='/'){
					if(s1[top1]==0){
						printf("NaN");
						return 0;
					}	
					temp=s1[top1-1]/s1[top1];
					top1-=2;
					s1[++top1]=temp;
					top2--;
				}
			}
			printf("%d",s1[top1]);
			break;
		}
		else if(str[i]>='0'&&str[i]<='9'){
			temp=0;
			while(str[i]>='0'&&str[i]<='9'){
				temp=temp*10+str[i]-'0';
				i++;
			}
			s1[++top1]=temp;
		}
		else{
			if(str[i]==')'&&s2[top2]=='('){
				top2--;
			}
			else if(top2==-1||str[i]=='('||s2[top2]=='('||((str[i]=='*'||str[i]=='/')&&(s2[top2]=='+'||s2[top2]=='-'))){
				s2[++top2]=str[i];
			}
			else if(str[i]==')'){
				while(s2[top2]!='('){
					temp=0;
					if(s2[top2]=='+'){
						temp=s1[top1-1]+s1[top1];
						top1-=2;
						s1[++top1]=temp;
						top2--;
					}
					else if(s2[top2]=='-'){
						temp=s1[top1-1]-s1[top1];
						top1-=2;
						s1[++top1]=temp;
						top2--;
					}
					else if(s2[top2]=='*'){
						temp=s1[top1-1]*s1[top1];
						top1-=2;
						s1[++top1]=temp;
						top2--;
					}
					else if(s2[top2]=='/'){
						if(s1[top1]==0){
						printf("NaN");
						return 0;
					}	
						temp=s1[top1-1]/s1[top1];
						top1-=2;
						s1[++top1]=temp;
						top2--;
					}
				}
				top2--;
			}
			else{
				temp=0;
				if(s2[top2]=='+'){
					temp=s1[top1-1]+s1[top1];
				    top1-=2;
					s1[++top1]=temp;
					top2--;
				}
				else if(s2[top2]=='-'){
					temp=s1[top1-1]-s1[top1];
					top1-=2;
					s1[++top1]=temp;
					top2--;
				}
				else if(s2[top2]=='*'){
					temp=s1[top1-1]*s1[top1];
					top1-=2;
					s1[++top1]=temp;
					top2--;
				}
				else if(s2[top2]=='/'){
					if(s1[top1]==0){
						printf("NaN");
						return 0;
					}	    
					temp=s1[top1-1]/s1[top1];
					top1-=2;
					s1[++top1]=temp;
					top2--;
				}
				i--;
			}
			i++;
		}
	}
	
	return 0;
}

解后反思： 可以从两个方面简化这段冗杂的代码：1.将从栈顶取两个元素然后用当前运算符计算得出结果的过程用函数进行模块化封装，这样可以减少很多重复的代码；2.给不同的运算符赋不同的值来表示它们的优先级，这样可以简单地通过’>’ ‘=’ '<'来比较它们的优先级。

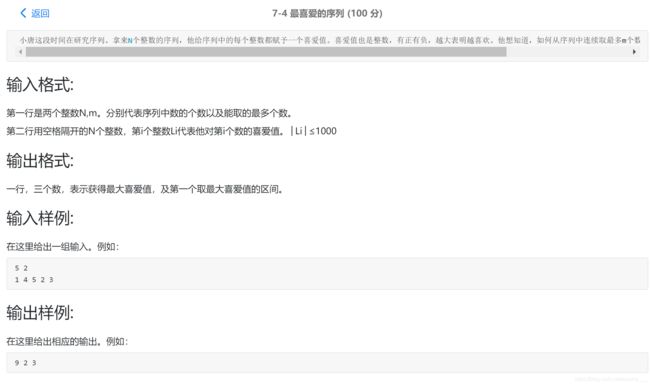
7-4 最喜爱的序列

原题呈现：

先上一版当时水到AC的代码：

#include
#include
#include
#include
#include

int a[500001],b[500001];

int main() {
	int  m, n, i,tmp=0,max,maxl,maxr;
	scanf("%d %d", &n, &m);
	int mm = m;
	while(mm>0){
	for (i = 0; i < mm; i++) {
		scanf("%d", &a[i]);
		tmp += a[i];
	}
	b[0] = tmp;
	if(mm==m){
	max = tmp;
	maxl = 1;
	maxr = mm;
	}
	for (i = mm; i < n; i++) {
		scanf("%d", &a[i]);
		tmp = b[i - mm] - a[i - mm] + a[i];
		b[i - mm + 1] = b[i - mm] - a[i - mm] + a[i];
		if (tmp > max) {
			max = tmp;
			maxl = i - mm + 2;
			maxr = i + 1;
		}
	}
	tmp = 0;
	mm--;
        if (mm > 10)
		break;
	}
    printf("%d %d %d", max, maxl, maxr);

	return 0;
}

这个方法能过完完全全是因为测试数据太水

下面给学习到的正确解法：

解题思路 ： 前缀和+单调优先队列

以下是根据这一思路写出的代码：

#include
using namespace std;
long long sum[500010];
deque<int> q;
int posl, posr;
int main()
{
    int n, m, i, j;
    scanf("%d %d", &n, &m);
    sum[0] = 0;
    for (i = 1; i <= n; i++)
    {
        scanf("%lld", &sum[i]);
        sum[i] += sum[i - 1];
    }//前缀和

    while (!q.empty())
        q.pop_back();
    //q.push_front(0);
    long long maxn = 0;
    for (i = 1; i <= n; i++)
    {
        while (!q.empty() && sum[q.front()] > sum[i])
        {
            q.pop_front();
        }
        q.push_front(i);//维护单调性
        while (!q.empty() && i - q.back() > m)
        {
            q.pop_back();
        }//维护区间长度不大于m
        int tmp = 0;
        if (q.back() == i) {
            tmp = sum[i] - sum[i - 1];
            if (maxn < tmp)
            {
                maxn = tmp;
                posl = i;
                posr = i;
            }
        }
        else {
            tmp = sum[i] - sum[q.back()];
            if (maxn < tmp)
            {
                maxn = tmp;
                posl = q.back() + 1;
                posr = i;
            }
        }
    }
    printf("%lld %d %d\n", maxn, posl, posr);
    return 0;
}

解后反思： 前缀和的思想其实不难想到，困难在于对单调队列的应用场景不熟悉。