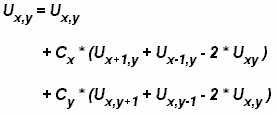【高性能计算背景】《并行计算教程简介》翻译 - 中文 - 4 / 4
目录
- 一、写在前面
- 二、摘要
-
- A. 并行计算概述
-
- 1. 什么是并行计算?
- 2. 为什么使用并行计算?
- 3. 谁在使用并行计算?
- B. 概念和术语
-
- 1. 冯诺依曼计算机体系结构
- 2. 弗林分类法
- 3. 通用并行计算术语
- 4. 并行编程的潜在好处、限制和成本
- C. 并行计算机内存架构
-
- 1. 共享内存
- 2. 分布式内存
- 3. 混合分布式共享内存
- D. 并行编程模型
-
- 1. 共享内存模型
- 2. 线程模型
- 3. 分布式内存/消息传递模型
- 4. 数据并行模型
- 5. 混合模型
- 6. SPMD 和 MPMP
- E. 设计并行程序
-
- 1. 自动并行 vs. 手动并行
- 2. 理解问题和程序
- 3. 分解
- 4. 通讯
- 5. 同步
- 6. 数据依赖
- 7. 负载均衡
- 8. 粒度
- 9. I/O
- 10. 调试
- 11. 性能分析和调优
- F. 并行示例
-
- 1. 数组处理
- 2. 计算PI
- 3. 简单热方程
- 4. 一维波动方程
- G. 参考资料和更多信息
- 四、总结
- 五、参考
一、写在前面
并行计算的入门文章非劳伦斯利弗莫尔国家实验室(LLNL)的《Introduction to Parallel Computing Tutorial》[1]所属,于是本着学习的态度,笔者对其进行了翻译,以下是《Introduction to Parallel Computing Tutorial》的中文版,篇幅限制,本篇博客仅包含F. 并行示例和G. 参考资料和更多信息部分,为《Introduction to Parallel Computing Tutorial》的第四部分,共四部分。
【高性能计算背景】《并行计算教程简介》翻译 - 中文 - 1 / 4
【高性能计算背景】《并行计算教程简介》翻译 - 中文 - 2 / 4
【高性能计算背景】《并行计算教程简介》翻译 - 中文 - 3 / 4
【高性能计算背景】《并行计算教程简介》翻译 - 中文 - 4 / 4
二、摘要
这是“利弗莫尔计算入门”研讨会的第一篇教程。本文旨在简要概述并行计算这一广泛而宽泛的主题,作为后续教程的导读。因此,它只涵盖并行计算的基本知识,面向刚刚熟悉该主题并计划参加本研讨会的一个或多个其他教程的人。它并不打算深入讨论并行编程,因为这将需要更多的时间。本教程首先讨论并行计算 - 它是什么以及如何使用,然后讨论与并行计算相关的概念和术语。然后探讨了并行内存体系结构和编程模型的主题。这些主题之后是一系列关于设计和运行并行程序的复杂问题的实际讨论。本教程最后给出了几个如何并行处理几个简单问题的示例。包括参考文献,以供进一步自学。
A. 并行计算概述
1. 什么是并行计算?
2. 为什么使用并行计算?
3. 谁在使用并行计算?
B. 概念和术语
1. 冯诺依曼计算机体系结构
2. 弗林分类法
3. 通用并行计算术语
4. 并行编程的潜在好处、限制和成本
C. 并行计算机内存架构
1. 共享内存
2. 分布式内存
3. 混合分布式共享内存
D. 并行编程模型
1. 共享内存模型
2. 线程模型
3. 分布式内存/消息传递模型
4. 数据并行模型
5. 混合模型
6. SPMD 和 MPMP
E. 设计并行程序
1. 自动并行 vs. 手动并行
2. 理解问题和程序
3. 分解
4. 通讯
5. 同步
6. 数据依赖
7. 负载均衡
8. 粒度
9. I/O
10. 调试
11. 性能分析和调优
F. 并行示例
1. 数组处理
- 这个例子演示了二维数组元素的计算;函数在每个数组元素上求值。
- 每个数组元素上的计算独立于其他数组元素。
- 这个问题需要大量计算。
- 串行程序按顺序一次计算一个元素。
- 串行代码的形式可以是:
do j = 1,n
do i = 1,n
a(i,j) = fcn(i,j)
end do
end do
二维数组
- 要问的问题:
- 这个问题可以并行化吗?
- 如何划分问题?
- 是否需要通信?
- 是否存在任何数据依赖关系?
- 是否需要同步?
- 负载平衡会成为一个问题吗?
并行解决方案1
-
元素的计算相互独立,带来理想的并行解决方案。
-
数组元素均匀分布,以便每个进程拥有数组(子数组)的一部分。
- 分配方案被选择以实现高效的内存访问;例如,以单位步长遍历子数组(步长为1)。单位步长可最大限度地提高缓存/内存使用率。
- 由于希望能以单元步长遍历子数组,因此分配方案的选择一定程度上取决于编程语言。请参见块-周期分配图。
-
数组元素的独立计算确保任务之间不需要通信或同步。
-
由于工作量均匀分布在各个进程之间,因此不应该存在负载平衡问题。
-
数组分发后,每个任务执行对应于它拥有的数据的循环部分。
-
例如,显示了 Fortran(列优先)和 C(行优先)块分布:
列优先:
do j = mystart, myend
do i = 1, n
a(i,j) = fcn(i,j)
end do
end do
行优先:
for i (i = mystart; i < myend; i++) {
for j (j = 0; j < n; j++) {
a(i,j) = fcn(i,j);
}
}
一种可能的解决方案:
- 作为单程序多数据(SPMD)模型实现——每个任务执行相同的程序。
- 主进程初始化数组,将信息发送给工作进程并接收结果。
- 工作进程接收信息,执行其共享的计算,并将结果发送给主进程。
- 使用Fortran存储方案,使用数组的块分布。
- 解决方案的伪代码:
红色强调了并行化更改。
示例程序
- MPI Array Program in C
- MPI Array Program in Fortran
并行解决方案2:任务池
-
之前的数组解决方案展示了静态负载均衡:
- 每个任务拥有固定数量的工作去做
- 对于速度更快或负载更轻的处理器来说,空闲时间可能很长——最慢的任务决定了总体性能。
-
如果所有任务在相同的机器上执行相同的工作量,静态负载平衡通常不是主要考虑。
-
如果您有负载平衡问题(某些任务的工作速度比其他任务快),您可以使用
任务池方案。
任务池方案
- 使用两个进程
主进程
- 保存工作进程要执行的任务池
- 当收到请求时向工作进程发送任务
- 收集工作进程的结果
工作进程
- 从主进程获取任务
- 执行计算
- 将结果发送给主进程
讨论
- 在上面的任务池示例中,每个任务计算一个单独的数组元素作为作业。计算与通信的比率非常精细。
- 细粒度解决方案会产生更多的通信开销,以减少任务空闲时间。
- 一个更好的解决方案可能是为每个作业分配更多的工作。
正确的工作量取决于问题本身。
2. 计算PI
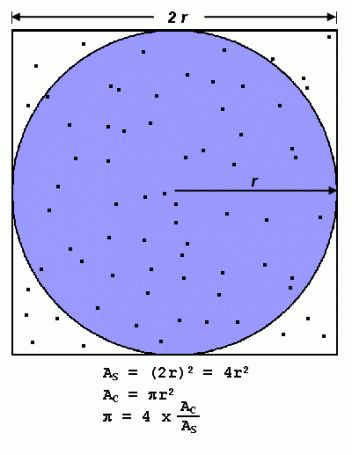
- PI 的值可以通过多种方式计算。考虑近似 PI 的蒙特卡洛方法:
- 在边长为 2 r 2r 2r的正方形上内接一个半径为 r r r的圆
- 圆的面积是 π r 2 π r^2 πr2,正方形的面积是 4 r 2 4r^2 4r2
- 圆的面积与正方形的面积之比为:
π r 2 / 4 r 2 π r^2 / 4r^2 πr2/4r2 = π / 4 π / 4 π/4 - 如果您在正方形内随机生成N个点,则大约 ( N ∗ π ) / 4 (N*π)/ 4 (N∗π)/4个点 ( M ) 应该落在圆内。
然后 π π π 的值近似为:
( N ∗ π ) / 4 = M (N*π) / 4 = M (N∗π)/4=M
π / 4 = M / N π / 4 = M / N π/4=M/N
π = 4 ∗ M / N π = 4 * M / N π=4∗M/N
请注意,增加生成的点数会提高近似值。
串行计算PI
- 此过程的串行伪代码:
npoints = 10000
circle_count = 0
do j = 1,npoints
generate 2 random numbers between 0 and 1
xcoordinate = random1
ycoordinate = random2
if (xcoordinate, ycoordinate) inside circle
then circle_count = circle_count + 1
end do
PI = 4.0*circle_count/npoints
- 问题是计算密集型的,大部分时间都花在执行循环上
- 要问的问题:
- 这个问题可以并行化吗?
- 如何划分问题?
- 是否需要通信?
- 是否存在任何数据依赖关系?
- 是否需要同步?
- 负载平衡会成为一个问题吗?
并行解决方案
-
又一个易于并行化的问题:
- 所有点计算都是独立的;无数据依赖关系
- 工作可以平均分配;无负载平衡问题
- 任务之间无需通信或同步
-
并行策略:
- 将循环划分为可由任务池执行的相等部分
- 每个任务独立执行其工作
- 使用SPMD模型
- 一个任务充当主任务来收集结果并计算PI的值
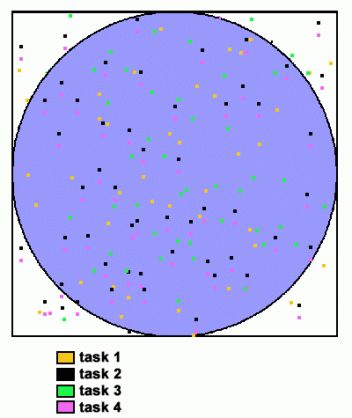
并行计算PI
示例程序
- MPI Pi Calculation Program in C
- MPI Pi Calculation Program in Fortran
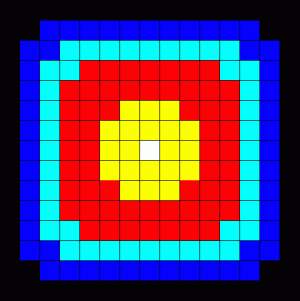
3. 简单热方程
有限差分格式
二维热问题
-
并行计算中的大多数问题都需要任务之间的通信。许多常见问题需要与
邻居任务进行通信。 -
给定初始温度分布和边界条件,二维热方程描述了温度随时间的变化。
-
采用有限差分格式在正方形区域上数值求解热方程。
- 二维数组的元素表示正方形上各点的温度。
- 边界处的初始温度为零,中间的初始温度为高。
- 边界温度保持在零度。
- 采用时间步进算法。
-
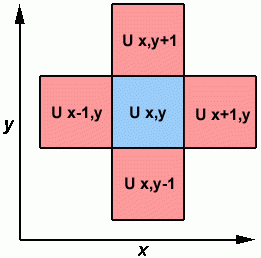
元素的计算依赖于相邻元素的值:
上述各项的计算
- 串行程序将包含如下代码:
do iy = 2, ny - 1
do ix = 2, nx - 1
u2(ix, iy) = u1(ix, iy) +
cx * (u1(ix+1,iy) + u1(ix-1,iy) - 2.*u1(ix,iy)) +
cy * (u1(ix,iy+1) + u1(ix,iy-1) - 2.*u1(ix,iy))
end do
end do
- 要问的问题:
- 这个问题可以并行化吗?
- 如何划分问题?
- 是否需要通信?
- 是否存在任何数据依赖关系?
- 是否需要同步?
- 负载平衡会成为一个问题吗?
并行解决方案
-
这个问题更具挑战性,因为存在需要通信和同步的数据依赖关系。
-
整个数组被划分并作为子数组分发给所有任务。每个任务在整个数组中拥有相等的份额。
-
因为工作量是相等的,所以不应该考虑负载平衡。
-
确定数据相关性:
- 属于任务的内部元素独立于其他任务
- 边界元素依赖于相邻任务的数据,因此需要进行通信。
-
作为SPMD模型实施:
- 主进程将初始信息发送给工作进程,然后等待从所有工作进程收集结果。
- 工作进程在指定的时间步数内计算解决方案,必要时与相邻进程通信。
-
解决方案的伪代码:
红色强调了并行化更改。
样例程序
- MPI Heat Equation Program in C
- MPI Heat Equation Program in Fortran
4. 一维波动方程
- 在此示例中,在经过指定的时间后,计算沿均匀振动管柱的振幅。
- 计算包括:
- y y y轴上的振幅
- x x x轴上的位置索引 i i i
- 沿着波动曲线的节点
- 以离散时间步更新振幅。
一维波动问题
- 要求解的方程是一维波动方程:
A(i,t+1) = (2.0 * A(i,t)) - A(i,t-1) + (c * (A(i-1,t) - (2.0 * A(i,t)) + A(i+1,t)))
其中c是常数
-
请注意,振幅将取决于之前的时间步(t,t-1)和相邻点(i-1,i+1)。
-
要问的问题:
- 这个问题可以并行化吗?
- 如何划分问题?
- 是否需要通信?
- 是否存在任何数据依赖关系?
- 是否需要同步?
- 负载平衡会成为一个问题吗?
一维波动方程并行解决方案
- 这是涉及数据依赖性的问题的另一个例子。并行解决方案将涉及通信和同步。
- 整个振幅阵列被划分并作为子数组分布到所有任务。每个任务在整个数组中拥有相等的份额。
- 负载平衡:所有的点都需要相等的工作,所以这些点应该平均分配。
- 块分解将把工作划分为多个任务作为块,允许每个任务拥有大部分连续的数据点。
- 通信只需要在数据边界上进行。块大小越大,通信越少。
一维波动问题的并行解法
样例程序
- MPI Concurrent Wave Equation Program in C
- MPI Concurrent Wave Equation Program in Fortran
本教程到此结束。
G. 参考资料和更多信息
-
作者:Blaise Barney, Livermore Computing (retired), Donald Frederick, LLNL
-
Contact: hpc-tutorials@llnl.gov
-
在网上搜索“并行编程”或“并行计算”将产生各种各样的信息。
-
推荐阅读——并行编程:
- “Designing and Building Parallel Programs”, Ian Foster - from the early days of parallel computing, but still illuminating.
http://www.mcs.anl.gov/~itf/dbpp/ - “Introduction to Parallel Computing”, Ananth Grama, Anshul Gupta, George Karypis, Vipin Kumar.
- University of Oregon - Intel Parallel Computing Curriculum
https://ipcc.cs.uoregon.edu/curriculum.html - UC Berkeley CS267, Applications of Parallel Computing, Prof. Jim Demmel, UCB – https://sites.google.com/lbl.gov/cs267-spr2020
- Udacity CS344: Intro to Parallel Programming - https://developer.nvidia.com/udacity-cs344-intro-parallel-programming
- “Programming on Parallel Machines”, Norm Matloff, UC Davis: http://heather.cs.ucdavis.edu/~matloff/158/PLN/ParProcBookS2011.pdf
- Cornell Virtual Workshop: Parallel Programming Concepts and High-Performance Computing - https://cvw.cac.cornell.edu/Parallel/
- CS267, Applications of Parallel Computers, Spring 2021, Prof. Jim Demmel, UCB - https://sites.google.com/lbl.gov/cs267-spr2021
- Introduction to High Performance Scientific Computing", Victor Eijkhout, TACC - https://pages.tacc.utexas.edu/~eijkhout/istc/istc.html
- COMP 705: Advanced Parallel Computing (Fall, 2017), SDSU, Prof. Mary Thomas - https://edoras.sdsu.edu/~mthomas/f17.705
- Georg Hager’s SC '20 Tutorial on Node-Level Performance Tuning - https://blogs.fau.de/hager/tutorials/sc20
- “Designing and Building Parallel Programs”, Ian Foster - from the early days of parallel computing, but still illuminating.
-
推荐阅读——Linux:
- An Introduction to Linux - https://cvw.cac.cornell.edu/Linux/
- Linux Tutorial for Beginners: Introduction to Linux Operating System - https://www.youtube.com/watch?v=V1y-mbWM3B8
- “Introduction to Linux” - Boston University - https://www.bu.edu/tech/files/2018/05/2018-Summer-Tutorial-Intro-to-Linux.pdf
-
照片/图片由作者创建,由其他LLNL员工创建,从非版权、政府或公共领域获得(例如http://commons.wikimedia.org/)来源,或在其他演示文稿和网页的作者许可下使用。
-
历史:这些材料从以下来源演变而来,不再保存或可用。
- 教程来自Maui High Performance Computing Center的“SP Parallel Programming Workshop”。
- he Cornell University Center for Advanced Computing (CAC)开发了教程,现可在以下网址作为Cornell Virtual Workshops提供:https://cvw.cac.cornell.edu/topics.
四、总结
以上就是今天要分享的内容,笔者没想到翻译工作居然要花费那么长的时间,原计划分为三部分后来发现篇幅有限制,只能改成四部分,本章节由浅入深的从理论和伪代码层面分析了四个并行计算的例子,同时也教会了读者书写并行程序时要学会这样思考:
- 这个问题可以并行化吗?
- 如何划分问题?
- 是否需要通信?
- 是否存在任何数据依赖关系?
- 是否需要同步?
- 负载平衡会成为一个问题吗?
本文翻译了《并行计算教程简介》的F章节,笔者一人翻译难免有翻译的不足之处,望海涵 。
如果本文能给你带来帮助的话,点个赞鼓励一下作者吧!
五、参考
[1] Lawrence Livermore National Laboratory:https://hpc.llnl.gov/documentation/tutorials/introduction-parallel-computing-tutorial