【LeetCode-中等】64. 最小路径和（图文详解）

题目

给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

题目地址：https://leetcode.cn/problems/minimum-path-sum/

方法1：暴力遍历（超时）

作者：本人

思路：

拿到这道题，本菜鸟就想着遍历，但感觉遍历也不好写，得用递归遍历。

        从数组第一个元素开始 向下或者向右走，累加得到sum，当走到右下角时，比较sum 和 minSum ，更新minSum为小的那个值。

        思路非常简单，但是代码对与新手来说不好写，因为要写递归。

class Solution {
    public int minPathSum(int[][] grid) {
       return helper( grid, 0, 0, 0, 99999999);
    }

    private int helper(int[][] grid, int a, int b, int sum, int minSum) {
        sum = sum + grid[a][b];
        //走到底了
        if (a == grid.length-1 && b == grid[0].length-1){
            minSum = Math.min(sum,minSum);
            return minSum;
        }
        //向右走到底了，那就向下走
        if (b == grid[0].length-1 ){
            minSum = helper( grid, a+1, b, sum, minSum);//向下走
        //向下走到底了，那就向右走
        }else if (a == grid.length-1){
            minSum = helper( grid, a, b+1, sum, minSum);//向右走

        }else {
            minSum = helper( grid, a, b+1, sum, minSum);//向右走
            minSum = helper( grid, a+1, b, sum, minSum);//向下走


        }
        return minSum;


    }

 效果

不通过，超出了时间限制

方法2：动态规划

        由于路径的方向只能是向下或向右，因此

                网格的第一行的每个元素：只能从左上角元素开始向右移动到达，网格的第一列的每个元素只能从左上角元素开始向下移动到达，此时的路径是唯一的，因此每个元素对应的最小路径和即为对应的路径上的数字总和。

                对于不在第一行和第一列的元素：可以从其上方相邻元素向下移动一步到达，或者从其左方相邻元素向右移动一步到达，元素对应的最小路径和等于其上方相邻元素与其左方相邻元素两者对应的最小路径和中的最小值加上当前元素的值。由于每个元素对应的最小路径和与其相邻元素对应的最小路径和有关，因此可以使用动态规划求解。

---

换句好理解的话说：

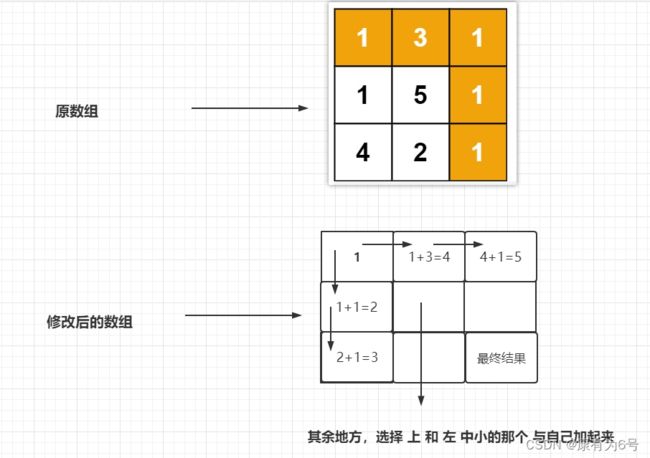
                第一行的数，只能由它左边的数累加过来

                第一列的数，只能由它上面的数累加过来

                而其他的数，可以从它上面累加，也能从它左面累加，我们选择二者中小的那边累加

        遍历数组，根据上面的三中方法，把每个数组的元素改写，最后左下角的那个数，就是结果。

动态规划 三步走

动态规划，就是利用历史记录，来避免我们的重复计算。而这些历史记录，我们得需要一些变量来保存，一般是用一维数组或者二维数组来保存。下面我们先来讲下做动态规划题很重要的三个步骤，

1.定义dp数组

我们会用一个数组，来保存历史数组，假设用一维数组 dp[] 吧。这个时候有一个非常重要的点，就是规定你这个数组元素的含义，例如你的 dp[i] 是代表什么意思？

2.找出递推关系式

动态规划类似于高中数学的数学归纳法，当我们要计算 dp[n] 时，是可以利用 dp[n-1]，dp[n-2]…..dp[1]，来推出 dp[n] 的，也就是可以利用历史数据来推出新的元素值，所以我们要找出数组元素之间的关系式，例如 dp[n] = dp[n-1] + dp[n-2]，这个就是他们的关系式了。

3.找出初始值

找出了递推公式，我们还需要初始值，因为递推公式就是靠前面的值推出后面的值，但总得有个头吧，这个头就是初始值。

提示

代码如何排错？将dp数组全部输出看看

对动态规划完全不会的同学可以先去做下面两道动态规划入门题

【LeetCode-简单】509. 斐波那契数（详解）

【LeetCode-简单】70. 爬楼梯（详解）

1.dp[i]:表示走到当前方格的最小路径

2.递推关系：每个方格的最小路径 = min(其上方方格的最小路径，其左方方格的最小路径)

3.初始值：dp[0][0] = grid[0][0]

 这道题不需要额外建立dp数组，直接在原数组上修改即可

class Solution {
    public int minPathSum(int[][] grid) {
        int m = grid.length;
        int n = grid[0].length;
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (i == 0 && j == 0){//初始化
                    continue;
                }else if (i == 0){//如果是上边界的（排除(0,0)）
                    grid[i][j] = grid[i][j] + grid[i][j-1];
                }else if (j == 0){//如果是左边界的（排除(0,0)）
                    grid[i][j] = grid[i][j] + grid[i-1][j];
                }else {//如果排除上边界和左边界的其他元素
                    grid[i][j] = grid[i][j] + Math.min(grid[i-1][j],grid[i][j-1]);
                }

            }
        }
        return grid[m-1][n-1];
    }
}

效果

总结

从这道题就能看出 算法和思路的重要性，一味地想着遍历，代码不好写，而且写出来时间复杂度也很高，但有一个很好的思路，代码也好些，机器运行的也快，多思考，多学习。