数据结构--》掌握数据结构中的排序算法
当我们面对海量数据时,如何高效地将其排序是数据结构领域中一个重要的问题。排序算法作为其中的关键部分,扮演着至关重要的角色。
无论你是初学者还是进阶者,本文将为你提供简单易懂、实用可行的知识点,帮助你更好地掌握排序算法在数据结构和算法中的重要性,进而提升算法解题的能力。接下来让我们开启数据结构与算法的奇妙之旅吧。
当我们需要对一组数据进行排序时,就需要使用排序算法。通常情况下,我们会将一组数据按照一定的规则进行排列,从而使其更易于查找和处理。
常见的排序算法包括冒泡排序、插入排序、选择排序、希尔排序、归并排序、快速排序等等。这些算法都有各自的优缺点,不同的应用场景适用不同的算法。因此,在实际开发中需要根据具体情况进行选择。接下来根据考研的大纲要求,着重对相关排序算法进行相应的讲解:
目录
插入排序
交换排序
选择排序
归并排序
基数排序
插入排序
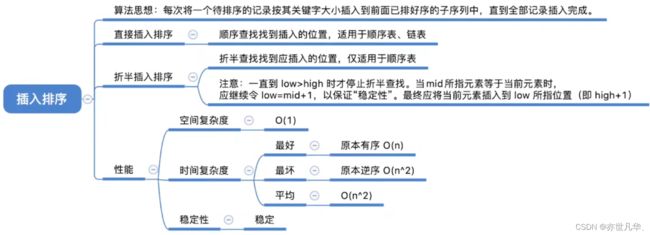
算法思想:每次将一个待排序的记录按其关键字大小插入到前面已排好序的子序列中,直到全部记录插入完成。其实现的过程大致如下:
1)从第一个元素开始,认为它是已排序的区间。
2)取出下一个元素,在已经排好序的元素序列中从后向前扫描。
3)如果该元素(已排序)大于新元素,将该元素移到下一个位置。
4)重复步骤 3 直到找到已经排序的元素小于或者等于新元素的位置。
5)将新元素插入到该位置中。
用c语言实现插入排序算法:
void insertionSort(int arr[], int n) {
int i, key, j;
for (i = 1; i < n; i++) {
key = arr[i];
j = i - 1;
while (j >= 0 && arr[j] > key) {
arr[j + 1] = arr[j];
j = j - 1;
}
arr[j + 1] = key;
}
}回顾重点,其主要内容整理成如下内容:
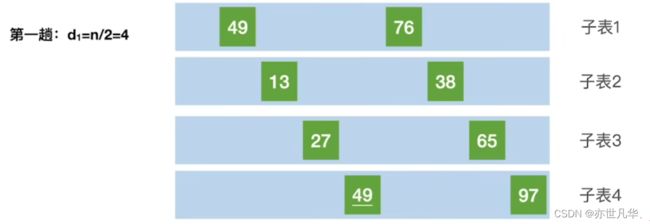
希尔排序:是一种基于插入排序的排序算法,也被称为缩小增量排序。它通过将待排序的元素分组,然后依次对每组的元素进行插入排序,最后再对整个序列进行一次插入排序。如下:
对生成的子表进行直接插入排序得到的结果如下:
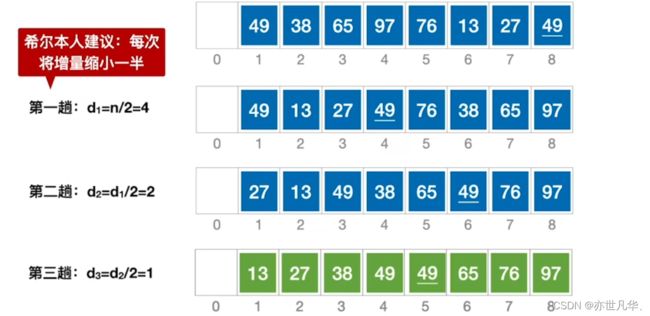
直到d等于1的时候,得到的排序结果基本有序,然后进行直接插入排序得到最后的结果。
最终呈现的过程结果如下:
用c语言实现希尔排序算法:
#include
void shellSort(int arr[], int n) {
// 定义增量序列
int gap, i, j, temp;
for (gap = n / 2; gap > 0; gap /= 2) {
// 内部使用插入排序对每个子序列进行排序
for (i = gap; i < n; i++) {
temp = arr[i];
j = i;
while (j >= gap && arr[j - gap] > temp) {
arr[j] = arr[j - gap];
j -= gap;
}
arr[j] = temp;
}
}
}
int main() {
int arr[] = {9, 5, 2, 7, 1, 8};
int n = sizeof(arr) / sizeof(arr[0]);
printf("原始数组:");
for (int i = 0; i < n; i++) {
printf("%d ", arr[i]);
}
shellSort(arr, n);
printf("\n排序后数组:");
for (int i = 0; i < n; i++) {
printf("%d ", arr[i]);
}
return 0;
} 回顾重点,其主要内容整理成如下内容:
交换排序
交换排序是一种比较简单直观的排序算法,其主要思想是通过交换数组中相邻且不符合顺序要求的元素,将最大或最小的元素逐步“冒泡”到正确的位置。常用的交换排序算法有冒泡排序和快速排序,下面将着重讲解一下这两种排序的相关实现:
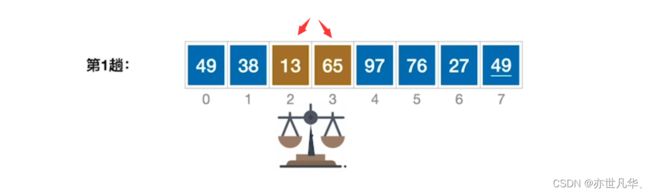
冒泡排序:最基础的交换排序算法,其核心思想是从左到右,依次比较相邻的元素,将较大的元素交换到后面。该算法重复多次,每次将一个未排序的元素放到正确的位置,直到整个数组有序。冒泡排序的时间复杂度为 O(n^2)。
前后数值进行对比,小的前大的后,然后重复多次,直到将顺序从小到大弄出来
用c语言实现冒泡排序算法:
#include
void bubbleSort(int arr[], int n) {
int i, j, temp;
for (i = 0; i < n-1; i++) {
for (j = 0; j < n-i-1; j++) {
if (arr[j] > arr[j+1]) {
// 交换相邻元素
temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}
}
}
int main() {
int arr[] = {9, 5, 2, 7, 1, 8};
int n = sizeof(arr) / sizeof(arr[0]);
printf("原始数组:");
for (int i = 0; i < n; i++) {
printf("%d ", arr[i]);
}
bubbleSort(arr, n);
printf("\n排序后数组:");
for (int i = 0; i < n; i++) {
printf("%d ", arr[i]);
}
return 0;
} 回顾重点,其主要内容整理成如下内容:
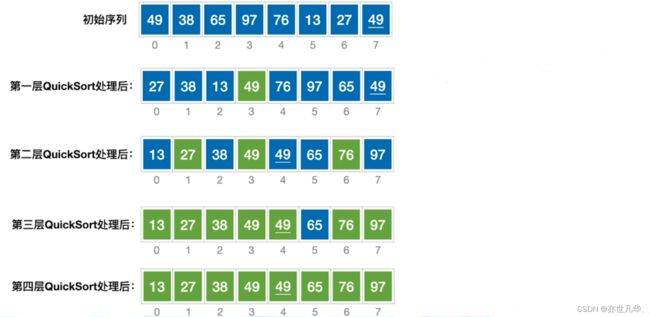
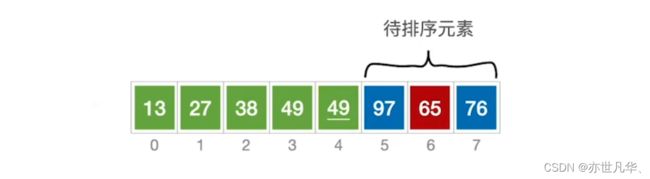
快速排序:是一种分治思想的排序算法,它将问题分割成较小的子问题,然后递归地求解这些子问题。在快速排序中,通过一趟排序将待排序的记录分割成独立的两部分,其中一部分记录的关键字均比另一部分记录的关键字小,然后再按此方法对两部分记录进行排序,递归地进行下去,直到整个序列有序。快速排序的平均时间复杂度为 O(n log n),最坏情况下时间复杂度为 O(n^2)。
用c语言实现快速排序算法:
#include
// 交换数组中两个元素的值
void swap(int* a, int* b) {
int temp = *a;
*a = *b;
*b = temp;
}
// 将基准元素放在正确的位置,并返回该位置的索引
int partition(int arr[], int low, int high) {
int pivot = arr[high]; // 将最后一个元素设为基准元素
int i = (low - 1); // i 初始化为最低索引的前一个
for (int j = low; j <= high - 1; j++) {
if (arr[j] < pivot) {
i++; // 找到一个比基准元素小的元素,将 i 向后移动
swap(&arr[i], &arr[j]); // 交换 arr[i] 和 arr[j]
}
}
swap(&arr[i + 1], &arr[high]); // 将基准元素放置在正确的位置
return (i + 1);
}
// 快速排序函数
void quickSort(int arr[], int low, int high) {
if (low < high) {
// 将基准元素放置在正确的位置
int pi = partition(arr, low, high);
// 递归调用快速排序函数
quickSort(arr, low, pi - 1); // 对基准元素左侧的子数组进行排序
quickSort(arr, pi + 1, high); // 对基准元素右侧的子数组进行排序
}
}
// 打印数组元素
void printArray(int arr[], int size) {
for (int i = 0; i < size; i++) {
printf("%d ", arr[i]);
}
printf("\n");
}
int main() {
int arr[] = {9, 5, 2, 7, 1, 8};
int n = sizeof(arr) / sizeof(arr[0]);
printf("原始数组:");
printArray(arr, n);
quickSort(arr, 0, n - 1);
printf("排序后数组:");
printArray(arr, n);
return 0;
} 回顾重点,其主要内容整理成如下内容:
选择排序
选择排序是一种简单直观的排序算法,它的基本思路是每次从未排序的部分中选择最小(或最大)的元素,然后将其放置在已排序部分的末尾。重复这个过程直到所有元素都排好序。常用的交换排序算法有简单选择排序和堆排序,下面将着重讲解一下这两种排序的相关实现:
简单选择排序:基本思路是每次从未排序的部分中选择最小(或最大)的元素,然后将其与未排序部分的第一个元素交换位置,即将最小元素放置在已排序部分的末尾。重复这个过程直到所有元素都排好序。
该算法的性能分析如下:
回顾重点,其主要内容整理成如下内容:
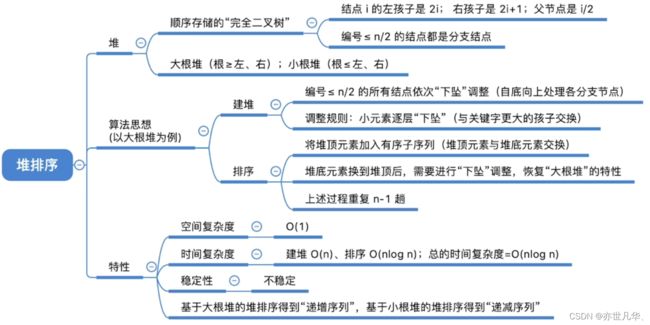
堆排序:
堆排序是一种基于堆数据结构的排序算法,它利用了堆的特性来进行排序。堆是一种完全二叉树,分为最大堆和最小堆两种类型。
关于堆排序的讲解可以参考我之前的文章:解锁数据结构中树与二叉树的奥秘(二) 中的堆排序讲解,总结知识如下:
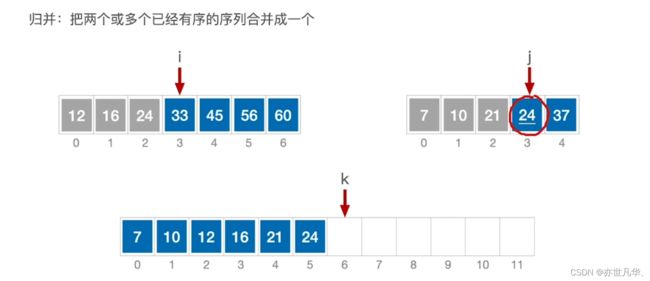
归并排序
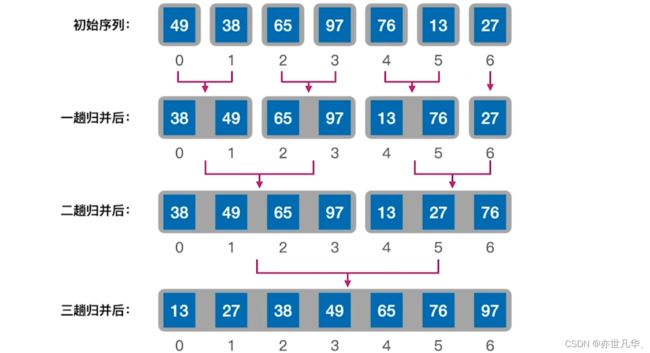
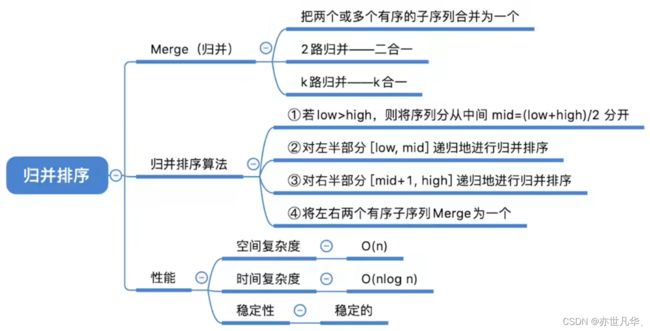
归并排序是一种常用的排序算法,它基于分治的思想。归并排序将待排序的数组不断分割为较小的子数组,然后逐步将这些子数组合并成为有序的大数组,最终得到完全有序的数组。如下:
手算模拟归并排序的过程如下:
回顾重点,其主要内容整理成如下内容:
基数排序
基数排序是一种非比较型整数排序算法,它是通过将待排序的整数按照位数划分成不同的数字组,然后对每个数字组进行排序,最终得到有序的整数数组。
得到的结果再以十位进行分配:
最终呈现的结果如下:
回顾重点,其主要内容整理成如下内容: