LeetCode 第4题：寻找两个正序数组的中位数（Python3解法）

1：问题描述

来源：LeetCode

难度：困难

---

问题详情：
给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。

算法的时间复杂度应该为 O(log (m+n)) 。

---

2：问题分析

对于中位数，假设一个数组长度为13，则我们需要找到第7个数；假设一个数组长度为14，则我们需要找到第7个和第8个数，然后求它们的平均值（从1开始计数）。

2.1 归并排序解法

首先想到的是对这两个数组进行合并后排序，然后找到对应位置的数值。
因为题目中说到两个数组都是正序数组，一个直观的解法就是，使用归并排序合并两个数组，归并排序的使用参考我的博文：归并排序合并两个有序数组(并附python实现)
。

这里就不再具体解释这种解法。
代码如下：

def findMedianSortedArrays(nums1, nums2):
    """
    将两个正序数组进行归并排序， 然后寻找归并后的数组中的中位数

    :param nums1:
    :param nums2:
    :return:
    """
    big_nums = []
    while nums1 or nums2:
        if nums1:
            t1 = nums1[0]
        else:
            big_nums.extend(nums2)
            break
        if nums2:
            t2 = nums2[0]
        else:
            big_nums.extend(nums1)
            break
        if t1 < t2:
            big_nums.append(nums1.pop(0))
        else:
            big_nums.append(nums2.pop(0))

    length = len(big_nums)
    if length % 2:
        median = big_nums[length // 2]
    else:
        median = (big_nums[length // 2] + big_nums[(length - 1) // 2]) / 2

    return median

当然，这种解法还有一些可优化之处，比如把对所有数据排序优化为只排序到需要的位置，比如两个数组总长度为13，我们只需排序到第7位即可，后面的数就不用再归并排序了。
这种解法代码如下：

def findMedianSortedArrays2(nums1, nums2):
    """
    与上述解法原理相同，不过只排序到中位数处，就停止

    :type nums1: List[int]
    :type nums2: List[int]
    :rtype: float
    """

    total_length = len(nums2) + len(nums1)
    max_index = total_length // 2

    big_nums = []
    while nums1 or nums2:
        if len(big_nums) == (max_index + 1):
            break
        t1 = t2 = 1e6
        if nums1:
            t1 = nums1[0]
        if nums2:
            t2 = nums2[0]
        if t1 < t2:
            big_nums.append(nums1.pop(0))
        else:
            big_nums.append(nums2.pop(0))

    if (total_length % 2) != 0:
        median = big_nums[-1]
    else:
        median = (big_nums[-2] + big_nums[-1]) / 2.0

    return median

上面的优化节省了一半的时间，但是实际想一想，我们并不需要前面一半非中位数位置的数，所以我们并不需要使用列表存储它们，因此就有如下优化：

def findMedianSortedArrays3(nums1, nums2):
    """
    与上述解法2原理相同，不过不存储非中位数的数值

    :param nums1:
    :param nums2:
    :return:
    """

    length = len(nums1) + len(nums2)
    # 如果长度之和为奇数，则需要获得第length//2下标的数值即是中位数
    if length % 2:
        need_dict = {length // 2: 0}
    # 如果长度之和为偶数，则需要获得第length//2下标和length//2 - 1的数值
    else:
        need_dict = {length // 2: 0, length // 2 - 1: 0}

    cur_index = -1  # 大数组中的索引，只不过下边并没有实际得到大数组
    changed = 0  # 一共找到了几个需要的数值
    while nums1 or nums2:
        t1 = t2 = 1e6
        if nums1:
            t1 = nums1[0]
        if nums2:
            t2 = nums2[0]
        if t1 < t2:
            pop_value = nums1.pop(0)
        else:
            pop_value = nums2.pop(0)
        cur_index += 1
        if cur_index in need_dict:
            need_dict[cur_index] = pop_value
            changed += 1
            if changed == len(need_dict):
                break

    total = 0.
    for item in need_dict.values():
        total += item

    median = total / len(need_dict)

    return median

如此一来，空间复杂度就从前面两种的O(m+n)优化到了O(1),但是很遗憾，基于归并排序的这三种解法的时间复杂度都是O(m+n),不符合题目中时间复杂度O(log(m+n))的要求。

2.2 二分查找解法

因为时间复杂度中存在log，（再加上看答案）不难想到使用基于二分查找的方法去求解该问题。
该方法的大概思想：将找中位数的问题转换为求解第k小问题，比如两个数组A和B总长度为3+4=7，那么需要寻找的中位数是其中的第4个数，所以我们要寻找第4小的数即可。

k = (m + n + 1) // 2, m 和 n分别表示两个数组的长度

假设总长度为奇数，那么该思路的正常情况（不考虑边界情况）的流程如下：

1. 通过比较k//2处的大小，然后删除较小方和其之前的数值
2. 使用k-删掉的数值数，因为已经删掉了一些比中位数要小的数值，所以我们的问题转换为了求第（k-删掉数个数）小，将k更新成（k-删掉数个数）
3. 再次重复1和2，直到k=1，然后比较两个数组的第一个位置的大小，比较小的就是要找的第k小

如果是总长度为偶数，则寻找第k小和第k+1小。

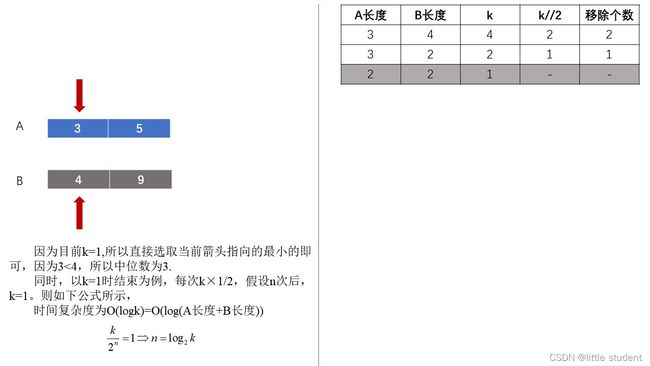
具体请看下图：

代码如下：

def findMedianSortedArrays4(nums1, nums2) -> float:
    def getKthElement(k):
        index1, index2 = 0, 0  # 这里的index都是从0开始计数的
        while True:
            # 如果index1 = m， 表示当前下标已经越界，说明该列表已经为‘空’，此时只需要查找剩下的列表的第k小数即可
            if index1 == m:
                return nums2[index2 + k - 1]
            if index2 == n:
                return nums1[index1 + k - 1]
            if k == 1:
                return min(nums1[index1], nums2[index2])

            # 正常情况
            newIndex1 = min(index1 + k // 2 - 1, m - 1)  # newIndex1表示当前需要对比的数值下标
            newIndex2 = min(index2 + k // 2 - 1, n - 1)
            pivot1, pivot2 = nums1[newIndex1], nums2[newIndex2]
            if pivot1 <= pivot2:
                k -= newIndex1 - index1 + 1
                index1 = newIndex1 + 1  # 而index1是当前列表从什么下标开始往后数k//2个，这里只是用下标模拟列表被删除的情况，不做真实的删除，
            else:
                k -= newIndex2 - index2 + 1
                index2 = newIndex2 + 1

    m, n = len(nums1), len(nums2)
    totalLength = m + n
    if totalLength % 2 == 1:
        return getKthElement((totalLength + 1) // 2)
    else:
        return (getKthElement(totalLength // 2) + getKthElement(totalLength // 2 + 1)) / 2

代码中使用index1的更新来模拟“被删除这一状态”,每次执行后index1都指向剩余数组的第一个位置。

边界问题：
如果一方已经“删除”所有数据，则只需取剩下的数组的第k小数即可。

时间复杂度的分析在最后一张图中，为O(log(m+n))