排序算法 - 基数排序图文解析实现

基数排序

基数排序（radix sort）属于“分配式排序”（distribution sort），又称“桶子法”（bucket sort）或bin sort，顾名思义，它是透过键值的部份资讯，将要排序的元素分配至某些“桶”中，藉以达到排序的作用，基数排序法是属于稳定性的排序，其时间复杂度为O
(nlog®m)，其中r为所采取的基数，而m为堆数，在某些时候，基数排序法的效率高于其它的稳定性排序法

简单来说，基数排序就是设置10个桶表示0~9，将要排序的元素先根据所有数的个位数分发到10个桶，然后按顺序重新返回数组，继续根据十位数分发。。。不断的分发到桶，然后顺序放回原来的数组，当所有位数都分发过了，数据就有序了

一个简单的数组[53,3,542,748,14,214]

基数排序是一个怎样的过程？

1. 准备好10个桶，表示0~9

2. 第一轮排序，根据个位数分发到10个桶，然后按照桶顺序、桶的数组顺序取回

3. 第二轮排序，根据十位数分发到10个桶（3默认为十位为0），然后按照桶顺序、桶的数组顺序取回（实际上桶里还有数据，我们通过改变指针，覆盖数据，使得桶逻辑上类似与没有数据）

4. 第三轮排序，根据百位数分发到10个桶（没有默认为百位为0），然后按照桶顺序、桶的数组顺序取回
   
5. 因为我们只有百位数据，到这里就结束排序了，实际上，应当判断数组数据的最高位

---

Java实现基数排序过程

根据上面的步骤，一步步实现基数排序

package com.company.sort;

import java.util.Arrays;

/**
 * @author zfk
 * 基数排序
 */
public class RadixSort {

    public static void main(String[] args) {
        int[] arr = {53,3,542,748,14,214};
        radixSort(arr);
    }

    public static void radixSort(int[] arr){


        //定义一个二维数组，表示10个桶
        //为了防止桶放入数的时候溢出，必须桶的大小必须为arr.length
        //基数排序是空间换时间
        int[][] bucket = new int[10][arr.length];
        //每个桶需要有一个指针，记录桶实际存放了多少个数据
        int[] bucketElementCounts = new int[10];

        //第一轮:取出元素的个位
        for (int j = 0;j < arr.length;j++){
            //求余数即可得到个位数
            int digitOfElement = arr[j] % 10;
            //放入桶中
            //第digitOfElement个桶(个位数)，第bucketElementCounts[digitOfElement](个位数)个指针指向的位置
            bucket[digitOfElement][bucketElementCounts[digitOfElement]] = arr[j];
            //该桶指针后移
            bucketElementCounts[digitOfElement]++;
        }
        //按照这个桶的顺序，取出所有数据放入原来的数组
        int index = 0;
        //遍历所有桶
        for (int k = 0;k < bucketElementCounts.length;k++){
            //如果桶中有数据，我们才放入原数组
            if (bucketElementCounts[k] != 0){
                //循环该桶，放回原数组
                for (int l = 0;l < bucketElementCounts[k];l++){
                    arr[index] = bucket[k][l];
                    index++;
                }
            }
            //处理后，需要将桶的指针置0
            bucketElementCounts[k] = 0;
        }

        System.out.println("第一轮，对个位的排序："+ Arrays.toString(arr));


        //第二轮:取出元素的十位
        for (int j = 0;j < arr.length;j++){
            //求余数，542/10 = 54 % 10 = 4
            int digitOfElement = arr[j] / 10 % 10;
            //放入桶中
            //第digitOfElement个桶(个位数)，第bucketElementCounts[digitOfElement](个位数)个指针指向的位置
            bucket[digitOfElement][bucketElementCounts[digitOfElement]] = arr[j];
            //该桶指针后移
            bucketElementCounts[digitOfElement]++;
        }
        //按照这个桶的顺序，取出所有数据放入原来的数组
        index = 0;
        //遍历所有桶
        for (int k = 0;k < bucketElementCounts.length;k++){
            //如果桶中有数据，我们才放入原数组
            if (bucketElementCounts[k] != 0){
                //循环该桶，放回原数组
                for (int l = 0;l < bucketElementCounts[k];l++){
                    arr[index] = bucket[k][l];
                    index++;
                }
            }
            //处理后，需要将桶的指针置0
            bucketElementCounts[k] = 0;
        }

        System.out.println("第二轮，对十位的排序："+ Arrays.toString(arr));

        //第二轮:取出元素的百位
        for (int j = 0;j < arr.length;j++){
            //求余数，542/100 = 5 % 10 = 5
            int digitOfElement = arr[j] / 100 % 10;
            //放入桶中
            //第digitOfElement个桶(个位数)，第bucketElementCounts[digitOfElement](个位数)个指针指向的位置
            bucket[digitOfElement][bucketElementCounts[digitOfElement]] = arr[j];
            //该桶指针后移
            bucketElementCounts[digitOfElement]++;
        }
        //按照这个桶的顺序，取出所有数据放入原来的数组
        index = 0;
        //遍历所有桶
        for (int k = 0;k < bucketElementCounts.length;k++){
            //如果桶中有数据，我们才放入原数组
            if (bucketElementCounts[k] != 0){
                //循环该桶，放回原数组
                for (int l = 0;l < bucketElementCounts[k];l++){
                    arr[index] = bucket[k][l];
                    index++;
                }
            }
            //处理后，需要将桶的指针置0
            bucketElementCounts[k] = 0;
        }

        System.out.println("第三轮，对百位的排序："+ Arrays.toString(arr));

    }
}

当然，上面是模拟过程，我们可以通过检测最高位，用循环简化

可以先遍历数组，得到最大的数，然后转为字符串求长度（当然，其他方法也可以）

public static void radixSort(int[] arr) {

        //定义一个二维数组，表示10个桶
        //为了防止桶放入数的时候溢出，必须桶的大小必须为arr.length
        //基数排序是空间换时间
        int[][] bucket = new int[10][arr.length];
        //每个桶需要有一个指针，记录桶实际存放了多少个数据
        int[] bucketElementCounts = new int[10];

        //先得到数组中最大的数的位数
        int max = arr[0];
        int length = arr.length;
        for (int i = 1; i < length; i++) {
            if (arr[i] > max) {
                max = arr[i];
            }
        }
        //得到最大位数
        int maxLength = (max + "").length();

        for (int i = 0, n = 1; i < maxLength; i++, n *= 10) {
            //对元素的 位数 分发排序 ，个位-》十位-》百位
            for (int j = 0; j < arr.length; j++) {
                //求余数即可得到个位值、十位值、百位
                int digitOfElement = arr[j] / n % 10;
                //放入桶中
                //第digitOfElement个桶(个位数)，第bucketElementCounts[digitOfElement](个位数)个指针指向的位置
                bucket[digitOfElement][bucketElementCounts[digitOfElement]] = arr[j];
                //该桶指针后移
                bucketElementCounts[digitOfElement]++;
            }
            //按照这个桶的顺序，取出所有数据放入原来的数组
            int index = 0;
            //遍历所有桶
            for (int k = 0; k < bucketElementCounts.length; k++) {
                //如果桶中有数据，我们才放入原数组
                if (bucketElementCounts[k] != 0) {
                    //循环该桶，放回原数组
                    for (int l = 0; l < bucketElementCounts[k]; l++) {
                        arr[index] = bucket[k][l];
                        index++;
                    }
                }
                //处理后，需要将桶的指针置0
                bucketElementCounts[k] = 0;
            }
            System.out.println("第" + (i + 1) + "轮排序：" + Arrays.toString(arr));
        }

    }

---

性能测试

基数排序时间复杂度为O (nlog®m)，其中r为所采取的基数，而m为堆数，在某些时候，基数排序法的效率高于其它的稳定性排序法

但是基数排序很明显就是空间换时间， 每次都需要创建10个和数组一样大的桶

随机生成8万0~80000的数进行排序：

public static void main(String[] args) {
        int[] arr = new int[80000];
        for(int i = 0 ;i <arr.length;i++){
            //随机生成80000内的整数
            arr[i] = (int) (Math.random()*80000);
        }

        Date dataBefore = new Date();

        radixSort(arr);

        Date dateAfter = new Date();

        System.out.println("消耗了："+(dateAfter.getTime()-dataBefore.getTime())+"ms");
    }

基数排序速度很快，在一定情况下效率最高

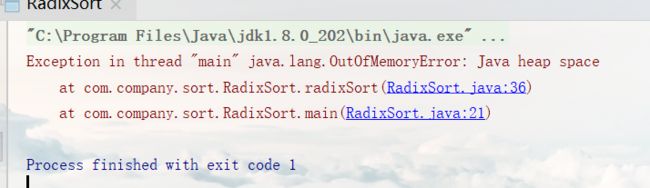
但当数据达到一定量，如八千万的数据，就会报错，内存不足OutOfMemoryError: Java heap space

---

关于负数的问题

其实，有负数的话不应该用桶排序的
但是，也是可以解决的：先判断有无负数，有则找到最小值，数组所有数据都减去该值（也就是加上最小值的绝对值，使得数组又是正数数组），接下来按正整数排序，最后数组所有数据加上原最小数 变为原有数据值

这样，就需要预处理数据，桶排序的效率就体现不出了，建议有负数时别用桶排序

---

MSD、LSD

这是两个概念（感觉是没必要划分的那么清楚）

• 最高位优先(Most Significant Digit first)法，简称MSD法：先按k1排序分组，同一组中记录，关键码k1相等，再对各组按k2排序分成子组，之后，对后面的关键码继续这样的排序分组，直到按最次位关键码kd对各子组排序后。再将各组连接起来，便得到一个有序序列。
• 最低位优先(Least Significant Digit first)法，简称LSD法：先从kd开始排序，再对kd-1进行排序，依次重复，直到对k1排序后便得到一个有序序列

就类似与一个从最高位，一个从最低位，都差不多