【LeetCode 算法专题突破】双指针(⭐)
文章目录
- 前言
- 1. 移动零
-
- 题目描述
- 代码
- 2. 复写零
-
- 题目描述
- 代码
- 3. 快乐数
-
- 题目描述
- 代码
- 4. 盛最多水的容器
-
- 题目描述
- 代码
- 5. 有效三角形的个数
-
- 题目描述
- 代码
- 6. 三数之和
-
- 题目描述
- 代码
- 7. 四数之和
-
- 题目描述
- 代码
- 总结
前言
学算法入门必学的一个章节,双指针算法,不说废话,直接开始。
1. 移动零
我们先来一道经典的双指针题目试试水
题目链接:283. 移动零
题目描述

怎么样才能在不创建新数组的情况下把 0 移动到数组的末尾呢?(如果不是有这个要求我肯定也无脑创建一个数组遍历解决)来看代码:
代码
func moveZeroes(nums []int) {
slow, fast := 0, 0
for fast < len(nums) {
if nums[fast] != 0 {
tmp := nums[fast]
nums[fast] = nums[slow]
nums[slow] = tmp
slow++
}
fast++
}
}
我们设置 slow,fast 两个指针,都从 0 开始遍历,fast 不断向后遍历查找不等于 0 的数交给 slow 位置,这样就会出现一种情况:
以 slow 为分界线,左边的区间都是排好的数字,右边就是没排好的数字,最后左边就排好了,而右边就都剩下 0 了
形象点说就是 fast 把数字都按序丢到了左边的区间
2. 复写零
像这样需要在数组中移动、删除、增加元素这类的操作,都是离不开双指针的算法思想
题目链接:1089. 复写零
题目描述

如果没有要求原地解决这道题目,也会非常的简单,但是如果需要我们原地求解,又好像有点无从下手了(如果使用 insert 方法来做这道题,那复杂度会非常的高)来看代码如何解决:
代码
func duplicateZeros(arr []int) {
left, right := 0, 0
// 找到一共经过了几个 0, 调整好位置
for right < len(arr) {
if arr[left] == 0 { // 注意这里用的是 left
right++
}
left++
right++
}
left--
right--
// 反向遍历
for left >= 0 {
if right < len(arr) {
arr[right] = arr[left]
}
if arr[left] == 0 { // 复写 0 的操作
right--
arr[right] = 0
}
left--
right--
}
}
这道题虽然是简单题,但是想要按照题目的要求来做出这道题并不容易,我们如果是第一次做,是很难想到使用反向迭代的双指针来做,所以还是重复我的一个观点:多刷算法,多积累,见多识广才能思路开阔。至少下一次遇到类似的题目我们就能匹配一下这个思路了。
回到正题,这道题如果使用双指针的话,需要我们从后往前迭代使用,直接用嘴说可能不太好理解,我给出的建议是,用题目给出的示例,然后对着代码把流程跑一遍,这样你能了解到这个算法的基本思路,可以看看图解:https://blog.csdn.net/Locky136/article/details/131537158
这里有两个需要注意的点:
- 一开始根据 left 经过多少个零来调整两个指针的位置(这里我用 left 和 right 命名是为了分辨两个指针的相对位置)
- 反向遍历时复写零的操作(为什么只复写了一次?因为还有一次和上一个操作合并了)
3. 快乐数
双指针还有一个非常重要的思想,就是快慢指针的思想,其实听名字大家差不多都能猜到具体的用法,但我们还是得来一道经典的题目试试水
题目链接:202. 快乐数
题目描述

这道题题意很好理解,所以我们直接根据示例,不说废话,直接上图:(题目的示例二,我们来模拟他的流程)
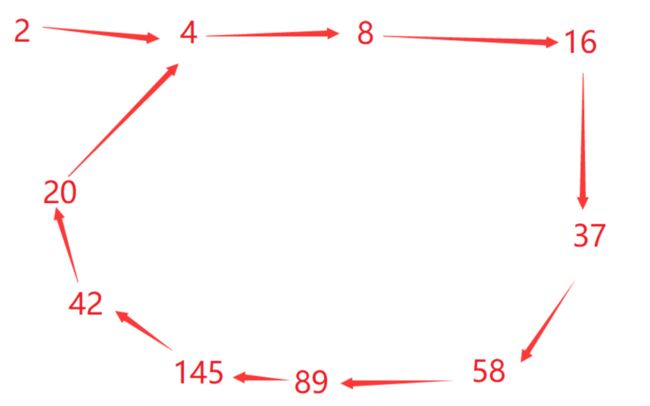
我们可以看到就像一个环,用快慢指针遍历,如果快指针追上了慢指针,那不就代表这段代码无限循环了吗?来看代码:
代码
func isHappy(n int) bool {
Sum := func(n int) int { // 进行一次快乐数的计算
sum := 0
for n > 0 {
tmp := n%10
sum += tmp*tmp
n /= 10
}
return sum
}
fast, slow := n, n
for {
slow = Sum(slow)
fast = Sum(Sum(fast))
if fast == slow {
break;
}
}
return fast == 1
}
其实这段算法的核心思想前面已经解释的很清楚了,这里就不赘述了,如果还有疑问跟着上面的图片走一遍代码就行~
4. 盛最多水的容器
再来一道经典的双指针题目练练手,如果没刷过这道题,你怎么敢说你刷过 LeetCode 呢~
题目链接:11. 盛最多水的容器
题目描述
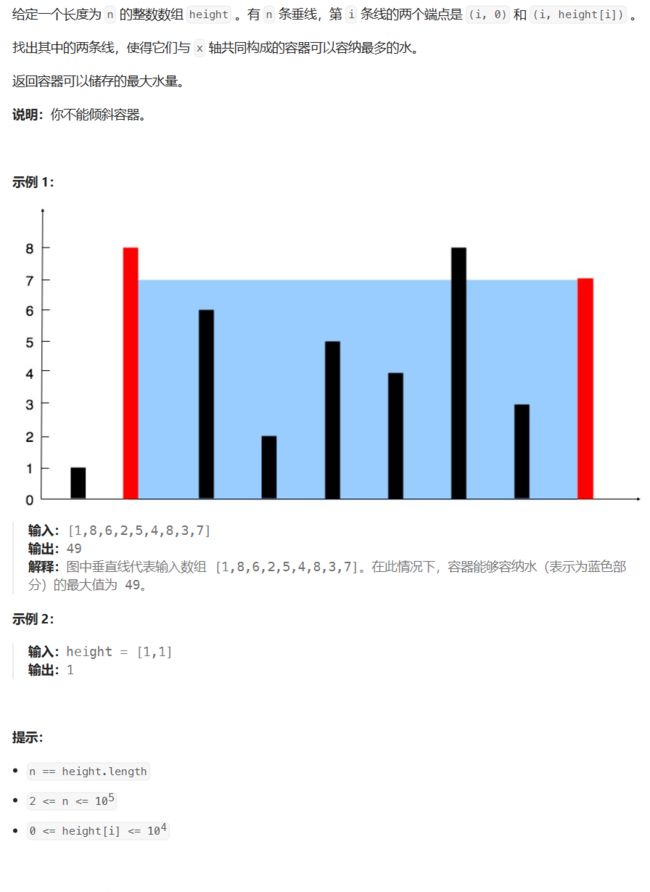
这道题的思路说难不难,说简单其实也不一定想的出来(首先把暴力排除,用暴力匹配就没意思了,更何况 10^5 的数据量用 O(N^2) 的算法不一定能过完这些样例,可能会超时(不然也不是中等难度的题目了))那我们就来看看怎么用双指针来做出这道题吧~
代码
func maxArea(height []int) int {
left, right, max := 0, len(height)-1, 0
for left < right {
tmp := Min(height[left], height[right])*(right-left) // 计算当前容量
max = Max(max, tmp) // 迭代出最大容量
if height[left] > height[right] {
right--
} else {
left++
}
}
return max
}
func Min(a, b int) int {
if a > b {
return b
}
return a
}
func Max(a, b int) int {
if a > b {
return a
}
return b
}
在解释思路之前必须吐槽一下 LeetCode 的 Golang 编译器,最新版本的 Go 其实已经实装了 max 和 min 让我们更方便的求最大值和最小值,但是我试了一下,LeetCode 的编译器并没有支持这个版本,搞得我只好自己写找最大最小值的方法,可恶
这道题其实知道想清楚核心的思路就很好做,left 和 right 指针分别在两边,我们只需要让比较矮的那一边的柱子移动即可,因为如果让较高的柱子移动,容量只可能更小,而让较矮的柱子移动:如果遇到更高的柱子,容量就可能更大。(这感觉也有一点贪心的思想在里面),根据分析,我们只要不断移动较矮的柱子,就能求出最大的容量了。
5. 有效三角形的个数
咱们再来做一道题目,练习双指针~
题目链接:611. 有效三角形的个数
题目描述

听完题意,有点算法经验的我们都能看出这道题目,如果使用暴力来做,那复杂度会非常的高,而且也并不好写,那我们该怎么设计算法来解决这道题目?来看代码:
代码
func triangleNumber(nums []int) int {
sort.Ints(nums)
ans := 0
for i := len(nums)-1; i >= 0 ; i-- {
left, right := 0, i-1
for left < right {
if (nums[left]+nums[right]) > nums[i] {
ans += (right-left)
right--
} else {
left++
}
}
}
return ans
}
这段代码的核心流程就是,将数组中最大的数作为三角形最长的那条边,也就是 i,利用三角形两边之长大于第三边的性质,快速找出符合要求的三角形,通过使用双指针的形式遍历余下的两条三角形的边
如果听完,代码也模拟完之后还有疑问的话,可以去看这篇文章,我曾经写过的详细文字解答,还配有清晰的图解:https://blog.csdn.net/Locky136/article/details/131590581
6. 三数之和
刷了这么多双支指针的题目了,怎么能错过 LeetCode 中大名鼎鼎的几数之和系列呢,两数之和,LeetCode 的第一道题,那是多少人刷题的起点,和梦想的开始呀,但是我们肯定不能还去做这么简单的题目,那必须是从三数之和开始刷起
题目链接:15. 三数之和
题目描述

这道题目其实并没有什么高深的技巧,抑或是复杂的算法,更多的是考察我们对代码的掌控能力,看看我们能不能写出一个像样的双指针算法,来看代码:
代码
func threeSum(nums []int) [][]int {
sort.Ints(nums)
var ans [][]int
n := len(nums)-1
for i, v := range nums[:n-1] {
if i != 0 && v == nums[i-1] { // 跳过重复数字
continue
}
if v+nums[i+1]+nums[i+2] > 0 { // 三数相加无论如何都会 > 0, 不需要再遍历
break
}
if v+nums[n]+nums[n-1] < 0 { // 三数最大值 < 0, 让 i 继续遍历
continue
}
// 双指针
left, right := i+1, n
for left < right {
s := v+nums[left]+nums[right]
if s > 0 {
right--
} else if s < 0 {
left++
} else {
ans = append(ans, []int{v, nums[left], nums[right]})
// 跳过重复数字
for left < right && nums[left] == nums[left+1] {
left++
}
for left < right && nums[right] == nums[right-1] {
right--
}
left++
right--
}
}
}
return ans
}
思路其实很简单,依旧是遍历一个 i,作为起点,用双指针匹配出符合题目要求的值,最后拼接在一起返回即可,这里需要注意的是我们需要根据题目的要求跳过重复的数字,不然最后还得去重,那反而就更麻烦了。
7. 四数之和
接下来就是我们练习双指针的最后一道题目啦,四数之和~
题目链接:https://leetcode.cn/problems/4sum/
题目描述

四数之和相较于三数之和,需要枚举的数字多了一个,我们只需要在三数之和的条件下,多枚举一个数即可,不过对代码掌控能力的要求也随之升高了不少,来看代码:
代码
func fourSum(nums []int, target int) [][]int {
sort.Ints(nums)
var ans [][]int
n := len(nums)-1
for a := 0; a < n-2; a++ {
value1 := nums[a]
if a != 0 && value1 == nums[a-1] { // 跳过重复数字
continue
}
if value1+nums[a+1]+nums[a+2]+nums[a+3] > target { // 四数之和 > target
break
}
if value1+nums[n-2]+nums[n-1]+nums[n] < target { // 四数最大和 < target
continue
}
for b := a+1; b < n-1; b++ {
value2 := nums[b]
if b != a+1 && value2 == nums[b-1] { // 跳过重复数字
continue
}
if value1+value2+nums[b+1]+nums[b+2] > target { // 四数之和 > target
break
}
if value1+value2+nums[n-1]+nums[n] < target { // 四数最大和 < target
continue
}
left, right := b+1, n
for left < right {
sum := value1+value2+nums[left]+nums[right]
if sum > target {
right--
} else if sum < target {
left++
} else {
ans = append(ans, []int{value1, value2, nums[left], nums[right]})
// 跳过重复数字
for left < right && nums[left] == nums[left+1] {
left++
}
for left < right && nums[right] == nums[right-1] {
right--
}
left++
right--
}
}
}
}
return ans
}
省流:其实跟三数之和换汤不换药,就是多加上了一层循环,仅此而已,代码一下就能看的出来。不过为了更好的掌控代码,我就没有再用 Golang 提供的语法糖,而是老老实实的用 for 循环了。
总结
我刷过的,个人喜欢的,比较经典的,数组相关的双指针问题大概就是这些了,其实双指针并不能算是一个标准的算法,我个人更倾向于这是一个思考的方向,一个算法的基本素养。为什么这么说呢?因为之后我们去做更多其他算法题,多多少少都会用到这样一个思想,在做链表专题的时候,也会用到双指针的思想
所以想要学好算法,打好每一步的基础都是非常重要滴~