AB实验核心知识点总结

一、AB实验的价值以及应用场景

AB实验目前已经是互联网以及泛互联网行业的标配，像字节这样的互联网大厂、元气森林这样的饮料公司都把AB实验作为产品功能迭代的重要的工具，它之所以如此重要是因为其能给出定性因果和定量增长两种核心价值，让产品快速迭代，从而实现增长。

1.1 定性因果

定性因果是指AB实验能够帮我们找到因果关系，知道策略对于目标是不是有直接作用，从而更有针对性的做产品优化和提升。它能够让我们以快速、较低的成本、较高的准确率验证因果关系，从而确保产品迭代和优化方向的正确性。

1.2 定量增长

定量增长是指AB实验能够量化因果效应。我们知道个体的因果效应不可识别，但是在随机化分组实验中，可以识别总体的因果效应ACE(Average Causal Effect)。用表示个体是否进行了某个实验，例如是否被投放了红点、是否被运营等，实验的个体取1，对照的个体取0。表示对个体进行实验和作为对照的潜在结果。表示一个用户没有被投放红点时的活跃度，表示一个用户被投放红点时的活跃度。表示个体接受实验后的个体因果作用。ACE可做如下改写：

其中 是实验对于参与实验人的平均因果效应，令是随机分组带来的选择偏差。如果AB实验分流足够均匀，实验组（T=1）和对照组（T=0）用户是同质的，这时选择偏差应该无限接近于0。可将其用更简单直观的方式：

T(实验效果) = T(实验组用户实验) - T(对照组用户不实验)

                        = [T(实验组用户实验) - T(实验组用户不实验) + T(实验组用户不实验) - T(对照组用户不实验)]

                        = T(实验组实验效果) + (选择偏差)

在AB实验对象随机分配的情况下，第一项为实验组用户接受实验和不接受实验的差异，第二项选择偏差的期望为0，所以可以用AB实验评估和量化因果关系。

1.3 AB实验的应用场景

二、AB实验的关键问题

2.1 保证选择偏差的期望是0

在1.2节AB实验效果拆解部分可以看到，保证AB随机分流均匀的重要性，如果实验组和对照组本身是有差异的，我们就无法确认实验是由实验对实验组用户的干预效果带来的还是由实验组和对照组用户本身差异带来的。所以保证参与实验对象被合理随机化是保证选择偏差是否为0的关键，这样实验结果就是由实验组对象由策略干预带来的提升。除此之外，实验之间对象独立不受影响也是保证实验效果是由实验组用户实验干预带来的关键。

2.2 正确理解AB实验涉及到的统计学知识

AB实验涉及到大量的统计学知识，从实验设计阶段的预估样本量到实验效果评估的假设检验、置信区间、p值等都是统计概念，需要正确的理解，才能保证推断的科学性。

三、AB实验涉及到的统计学知识

AB实验的本质是通过对总体用户抽样的一个小样本群体实验，基于这个小样本用户的实验效果回答实验带来的差异是否显著，以此来推断能否将其推广至更大的用户群体。这里边涉及到区间估计、置信区间、置信度、显著性水平、假设检验、统计分布、P值、第一/二类错误、功效、灵敏度MDE等，接下来就逐一介绍一下涉及到的概念。

3.1 点估计与区间估计

点估计是用样本统计量的某个取值直接作为总体参数的取值。区间估计是在点估计的基础上，给出总体参数估计的一个区间范围，该区间通常是由样本统计量加减估计误差得到的。

3.2 置信区间、置信水平、显著性水平

1) 置信区间

由样本区间构造的总体参数的估计区间就叫做置信区间。以总体样本均值的抽样分布为例，该分布服从均值为，标准误差为 的正态分布，根据正态分布的性质可知样本均值落在总体均值任何一个抽样标准差范围的概率。但实际往往我们不知道总体均值，知道的是样本均值。因此对于“样本均值落在总体均值1.96倍标准差范围内的概率是95%”这样的说法，可以改成，“约有95%的样本均值所构造的两个标准差区间包含总体均值”，这个区间就是置信区间。

2) 置信水平

置信水平也叫置信度或置信系数，以置信水平为95%为例，是指如果重复构造多次置信区间，则有95%的置信区间会包含总体参数真值，可以理解为描述实验结果的可信度。

3) 显著性水平

显著性水平α是人为定义的用于判断是否为小概率事件的阈值，如果低于该阈值，则认为是小概率事件，也是可以接受判断发生错误的概率。

3.3 假设检验

AB实验的涉及到的统计学知识主要围绕假设检验来，其核心思想是小概率事件在一次实验中几乎不可能发生，假设检验就是利用这个小概率事件的发生进行反证。其基本过程如下：

1) 做出一个假设H0(我们要推翻的假设)，以及它的备择假设H1(想要支持的假设)

2) 构造合适的检验统计量，通过检验统计量决策或者通过p值决策。

决策的本质是，观察小概率事件是否发生，如果发生了，我们就可以拒绝原假设H0，接受H1；如果没有发生，就不能拒绝H0。

3.3 如何判断统计显著性（假设检验如何决策）

统计显著性核心要回答的问题是，实验组和对照组是否有差异，如果有差异，这个差异是否是显著的。回答这个问题可以用检验统计量或P值两种方法。

1) 检验统计量决策

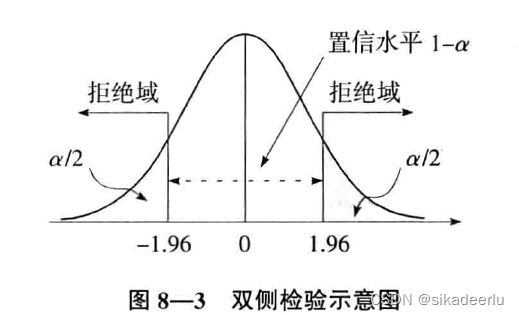
计算统计量类似于把一般得分转化为标准得分，如下以构造z分布为例，计算z统计量的值，根据下图来进行决策，如果原假设成立（A组、B组无差异），则95%的样本均值转化为z值后应该落在（-1.96， 1.96）之间。以作为小概率事件发生的阈值，如果z值落在下图的拒绝域中，就可以拒绝原假设。

 2) P值决策

用检验统计量决策的好处是确定了，其拒绝域也确定了，决策界限清晰。缺点是进行决策面临的风险是笼统的。z值等于2.5和z值等于2都落在了拒绝域，两者犯第一类错误的概率都是0.05，但两者面临的风险是不一样的，为了更精确的反应决策的风险度，可以用p值进行决策。

P值是指原假设为真时，随机抽取样本出现极端事件的概率，P值很小说明这个事件发生的概率很小，一旦出现了，根据小概率原理，我们就有理由拒绝原假设，P值越小拒绝原假设的的理由就越充分。用P值决策时，本身就代表了显著性水平，可以把P值和事先定义的显著性水平进行对比，如果小于就可以拒绝原假设。

3.4 第一类错误、第二类错误、功效

第一类错误：实验没效，但认为有效，上线了。即H0为真，却拒绝了。一般用显著性水平描述反第一类错误的概率。

第二类错误：实验有效，但认为无效，被否定了。即H0为假，却接受了。

功效：1 - 第二类错误的概率。功效的含义是，实验有效，我们有多大概率检测出来，即H0为假，做出拒绝H0的概率，一般将功效设置为80%。

3.5 最小样本量

最小样本量是指要想检测出预期的变化，至少需要多少样本才能满足。其计算公式为：

：显著性水平，一般为0.05，为1.96

：检验效能，一般为0.8，为0.84

：组合标准差

：组间差异，一般为实验组和对照组之间的预期差异。

带入公式后可得：

 3.7 AB实验的检验统计量

对于AB实验来说，我们要构造的是双总体均值之差的检验，对于双总体独立大样本，方差未知，用的是z分布来做检验，假设AB实验中A组的实验结果为，B组的实验结果为，我们要验证A组和B组实验结果是否有显著差异即是否等于0，则其要检验的统计量为：

火山引擎AB测试用的是t检验，t检验对于小样本、大样本都试用，具体可参考贾俊平老师统计学书中下图。

3.8 实验灵敏度MDE

MDE（Minimum Detectable Effect)，最小可检测单位，即实验灵敏度，是指实验在当前条件下能有效检测出的最小变化。以电商平台为例，某AB试验中实验组交易额较对照组提升0.5%，但试验平台只能检测出1%的变化，那么这个试验可能被认为不显著被放弃了。实际上，虽然试验效果提升较少，但确实带来了提升，却因误判被放弃了，因此提高实验灵敏度可更精确的评估收益。

1) 如何提高灵敏度

从统计学角度看实验灵敏度，其实就是我们对样本指标所在区间估计的准确程度。区间估计的越准，指标天然波动的范围控制得越小，我们就越有把握知道指标变化是实验带来的还是自然波动带来的，从而获得的实验灵敏度就越高。区间估计的边际误差由决定，所以可以通过增加样本量或者减小方差来提高实验灵敏度。增加样本较好理解，可以直接增加流量或拉长实验周期；减小方差可以从以下三个方面入手。

a. 选择指标，选择方差更小的指标（如用是否购买代替购买），或通过数据处理/标准化减小方差。

b.通过触发手段聚焦实验结果人群，排除非实验人群，从而减小方差。

c.在实验分组过程中，通过分层法、CUPED等方法减小因不同特征用户组间分配不均带来的方差，或者通过配对法减小方差。

四、AB实验平台核心功能

AB实验平台一般包含三个部分，实验管理和配置、实验部署和运行、实验数据分析。其交互过程如下：

实验管理和配置：通过用户界面或API定义、设置、管理实验，并存储在实验系统平台中。

实验部署和运行：客户端或服务端的实验部署包括变量赋值或参数化，即实验分流。

实验数据分析：包括日志记录、数据处理、指标定义和计算、p值、显著性、监控报警、数据可视化仪表盘等。

下图是AB平台通用参考框架：

4.1 随机分流核心功能

其中随机分流是产品发展到一定程度，支撑大量广泛实验的关键，更精细化的实验流量管理，能帮助我们精准调配、灵活调整平台用户流量，实现流量的充分利用，并且让实验结果更加科学。其中重点功能有单层分流、正交分层等。

1）单层分流

单层分流是指不重复利用用户，在同一时间内，一个用户最多只参与一个实验。在实验初期，实验数量较少，常采用单层分流模式。

2）正交分层

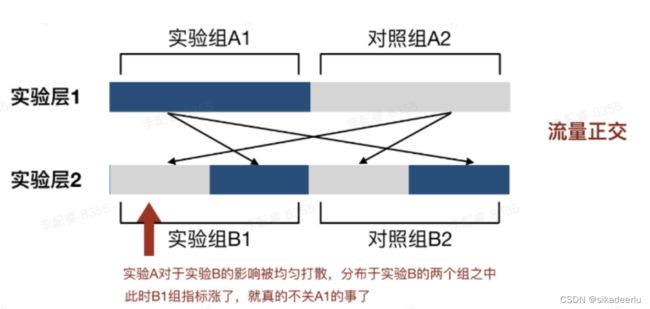
正交分层是为了解决单层分流流量不够用的问题，将实验扩展到单层之外，用户可同时进行多个实验。实验方法是拥有多个实验层，每一层的行为类似于单层方法，为了确保层与层之间的正交性，会对每一层添加层id也称为盐值，层与层之间之间的正交性通过散列函数加层id保证。正交分层中的每一层中的用户都能均匀的分配到其他各层中，各层之间不影响、不相交，都可单独使用，层与层之间的影响通过正交随机打散的方式被抵消了，因此每一层看到的仍然是这一层中该层特征的实验效果。如下图所示，实验A和实验B就实现了流量正交。

3）分多少层

正交分层能解决流量复用的问题，但分层不是越多越好，例如实验A是字体变红，实验B是字体变蓝，如果一个用户同时被两个实验命中，这个用户的字体则会变得很奇怪，对用户体验影响较大。为了避免类似糟糕的用户体验，可使用有限层划分方法，按照实验分类进行分层，组合在一起会形成较差用户体验的实验必须放在同一层。例如第一层用于UI元素实验，第二层用于内容实验，第三层用于后端实验，第四层用于算法实验等。

五、实验不显著怎么办

AB实验中经常遇到的问题是实验不显著，要怎么办，要怎么分析。我们从实验所需的样本量公式 可以看出，当检验效能（假定为80%，实验有效且能被检验出来的概率）不变时，要想检验出的越小，可以通过增加样本量或减小方差两种方法，以保证更小的变化被检测出来。

1）增加样本量是较常用也是较简单的方法，可以延长实验周期，也可直接扩大流量。

2）缩小方差可通过分层实验、CUPED、选择方差较小的指标等方法来解决。分层实验具体来说是指可通过对核心指标影响较大的特征进行分组，在每个分组里分别实验，这样可减小分组内实验的方差。

六、sql中如何进行显著性判断

对于双总体独立大样本的z检验，在sql中也可以实现，核心参考代码如下：

-- ab实验结果表
create table db.t0 (
    user_id string comment 'user_id'
    , ab_group string comment 'ab分组'
    , cnt string comment '指标'
) partitioned by (inc_day string comment '分区日期')
stored as parquet;



-- 指标均值方差
drop table db.t1;
create table db.t1 stored as parquet as
select
    ab_group
    , count(distinct user_id) user_cnt -- 用户数
    , avg(nvl(cnt,0)) cnt_avg -- 均值
    , stddev_pop(nvl(cnt,0)) cnt_std  -- 方差
from db.t0
group by ab_group;



-- 剔除3σ外的异常值 可按照实际情况修改
drop table db.t2;
create table db.t2 stored as parquet as
select
    t0.ab_group
    , count(distinct case when abs(nvl(cnt, 0) - cnt_avg) < 3*cnt_std then user_id else null end) user_cnt  -- 剔除异常值后用户数
    , avg(case when abs(nvl(cnt, 0) - cnt_avg) < 3*cnt_std then nvl(cnt, 0) else null end) cnt_avg  -- 剔除异常值后均值
    , stddev_pop(case when abs(nvl(cnt, 0) - cnt_avg) < 3*cnt_std then nvl(cnt, 0) else null end) cnt_std  -- 剔除异常值后方差
from db.t0 t0  -- 原始ab结果表
left join db.t1 t1  -- ab分组均值方差表
on t0.ab_group = t1.ab_group
group by t0.ab_group;



-- 实验组关联对照组
drop table db.t3;
create table db.t3 stored as parquet as
select t1.ab_group
    , t1.cnt_avg
    , t1.cnt_std
    , t1.user_cnt
    , t2.cnt_avg cnt_avg_b  -- 对照组 用户数
    , t2.cnt_std cnt_std_b  -- 对照组 均值
    , t2.user_cnt user_cnt_b  -- 对照组 方差
from db.t2 t 
left join (
    select * from db.t2 where ab_group = '对照组'
) t1  
on t1.ab_group = t2.ab_group
group by t1.ab_group;



-- 计算z值，判断显著
drop table db.t4;
create table db.t4 as
select
    ab_group 
    , user_cnt 
    , cnt_avg - cnt_avg_b cnt_avg_inc  -- 提升值
    , if(ABS((cnt_avg - cnt_avg_b)/SQRT(POWER(cnt_std, 2)/user_cnt + POWER(cnt_std_b, 2)/user_cnt_b)) > 1.65, 1, 0) cnt_significant  -- 是否显著
    , send_fee_avg/send_fee_avg_b - 1 send_fee_change_rate
from db.t3;

本文总结了AB实验中涉及到的一些基本问题，参考资料如下

1. 《AB实验：科学归因与增长的利器》 刘玉凤

2. 《统计学》贾俊平

3. 火山引擎AB测试文档：如何看懂实验报告--A/B测试-火山引擎