【C++】字典树（trie树）

引入

当我们走进图书馆的阅览室寻找书时，会不由自主地根据书架上的分类标签寻找自己所喜好的书籍；当打开电脑中的资源管理器时，我们会看到一层一层的目录结构。它们的存在，方便了我们生活中的一个重要的问题——检索。

在信息学竞赛（ Olympiad in Informatics ，简称 OI）的学习过程中，我们也经常会遇到关于“检索”的问题。而通常采用的不借助任何数据结构（Data Structure）的的枚举方法，虽然简单易写，但往往存在着效率低下的弊端。那我们如何才能通过简单的途径提高算法中的检索效率？

百科名片

在计算机科学中，trie，又称前缀树或字典树，是一种有序树，用于保存关联数组，其中的键通常是字符串。与二叉查找树不同，键不是直接保存在节点中，而是由节点在树中的位置决定。一个节点的所有子孙都有相同的前缀，也就是这个节点对应的字符串，而根节点对应空字符串。

例1 单词查找树

NOI-2000 Luogu-5755 CodeVS-1729
链接：
Luogu： https://www.luogu.com.cn/problem/P5755
CodeVS： http://codevs.cn/problem/1729/
CodeVS的链接给了好像没啥用

题目描述

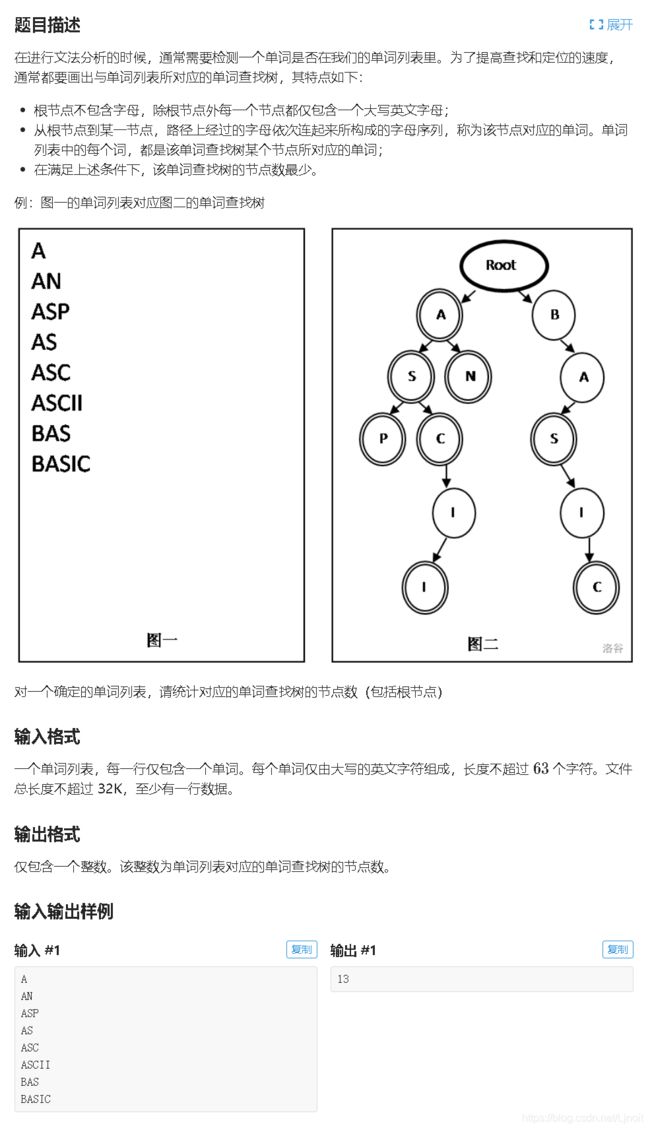
在进行文法分析的时候，通常需要检测一个单词是否在我们的单词列表里。为了提高查找和定位的速度，通常都要画出与单词列表所对应的单词查找树，其特点如下：

• 根节点不包含字母，除根节点外每一个节点都仅包含一个大写英文字母；
• 从根节点到某一节点，路径上经过的字母依次连起来所构成的字母序列，称为该节点对应的单词。单词列表中的每个词，都是该单词查找树某个节点所对应的单词；
• 在满足上述条件下，该单词查找树的节点数最少。

对一个确定的单词列表，请统计对应的单词查找树的节点数（包括根节点）。

输入描述

一个单词列表，每一行仅包含一个单词。每个单词仅由大写的英文字符组成，长度不超过 6363 个字符。文件总长度不超过 32K，至少有一行数据。

输出描述

仅包含一个整数。该整数为单词列表对应的单词查找树的节点数。

样例输入

A
AN
ASP
AS
ASC
ASCII
BAS
BASIC

样例输出

13

思路

字母树的插入（Insert）、删除（ Delete）和查找（Find）都非常简单，用一个一重循环即可，即第 i次循环找到前 i个字母所对应的子树，然后进行相应的操作。实现这棵字母树，我们用最常见的数组保存即可，当然也可以开动态的指针类型。至于结点对儿子的指向，一般有三种方法：

1 对每个结点开一个字母集大小的数组，对应的下标是儿子所表示的字母，内容则是这个儿子对应在大数组上的位置，即标号；

2 对每个结点挂一个链表，按一定顺序记录每个儿子是谁；

3 使用左儿子右兄弟表示法记录这棵树。

三种方法，各有千秋。第一种易实现，但实际的空间要求较大；第二种，较易实现，空间要求相对较小，但比较费时；第三种，空间要求最小，但相对费时且不易写。但总的来说，几种实现方式都是比较简单的，只要在做题时加以合理选择即可，本文不再赘述。

代码

和“思路”配套的代码：

#pragma GCC optimize(3,"Ofast","inline")
#pragma G++ optimize(3,"Ofast","inline")

#include 
#include 
#include 
#include 
#include 

#define R                  register int
#define re(i,a,b)          for(R i=a; i<=b; i++)
#define ms(i,a)            memset(a,i,sizeof(a))

using namespace std;

typedef long long ll;

int const N=1e5+5;

struct trie {
    int ch[26];
} tr[N];

int tot=0;
char s[110];

inline void cl(int k) {
    for(int i=0; i<26; i++) tr[k].ch[i]=0;
}

void insert() {
    int x=0,len=strlen(s);
    for(int i=0; s[i]; i++) {
        if(tr[x].ch[s[i]-'A']==0) {
            tr[x].ch[s[i]-'A']=++tot;
            cl(tot);
        }
        x=tr[x].ch[s[i]-'A'];
    }
}

int main(){
    while(scanf("%s",s)!=EOF) insert();
    printf("%d\n",tot+1);
    return 0; 
}

更简短的代码：

#pragma GCC optimize(3,"Ofast","inline")
#pragma G++ optimize(3,"Ofast","inline")

#include 
#include 
#include 
#include 
#include 

#define R                  register int
#define re(i,a,b)          for(R i=a; i<=b; i++)
#define ms(i,a)            memset(a,i,sizeof(a))

using namespace std;

typedef long long ll;

int const N=1e5+5;

int tot;
int t[N][26];
char s[65];

void insert(char *s) {
    int k=0;
    for(int i=0; s[i]; i++) {
        int x=s[i]-65;
        k=t[k][x] ? t[k][x]: t[k][x]=++tot;
    }
}

int main(){
    while(scanf("%s",s)!=EOF) insert(s);
    printf("%d\n",tot+1);
    return 0; 
}

正式开始介绍字典树

字典树，又称单词查找树、Trie树，是 一种树形结构，是一种哈希树的变种。典型应用是用于统计，排序和保存大量的字符串（但不仅限于字符串），所以经常被搜索引擎系统用于文本词频统计。它的优点是：利用字符串的公共前缀来节约存储空间，最大限度地减少无谓的字符串比较，查询效率比哈希表高。

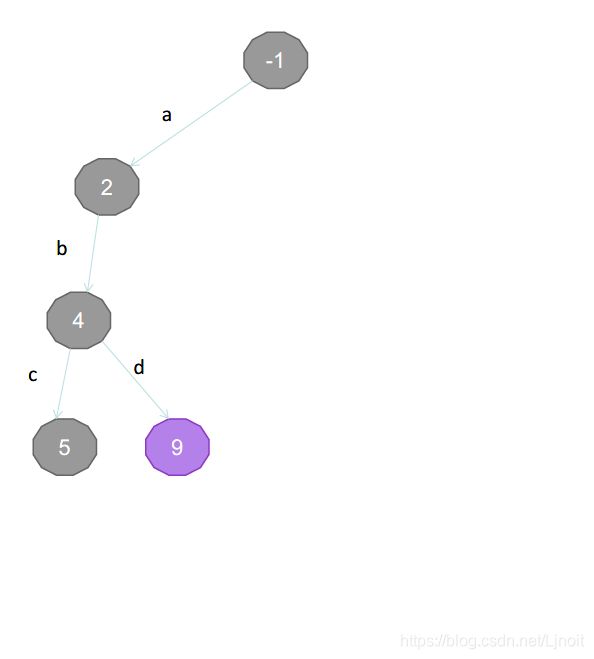
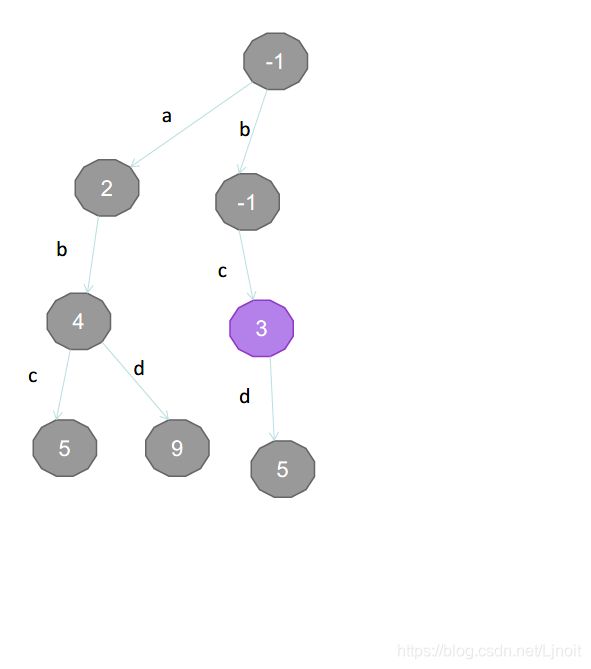
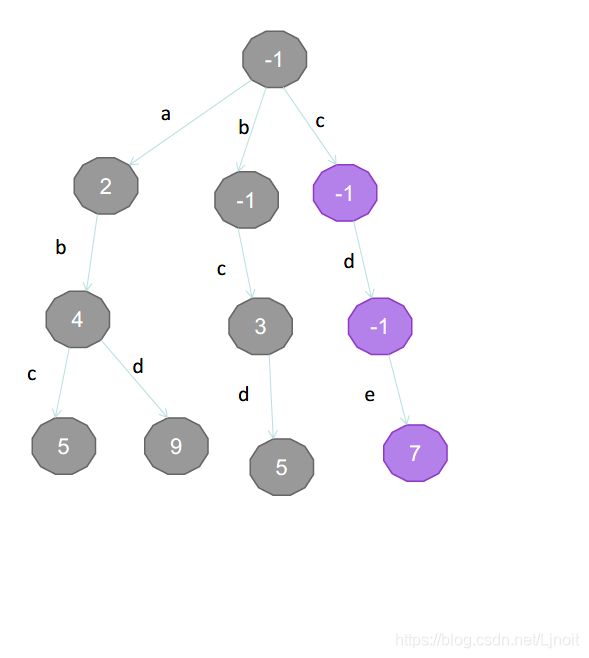
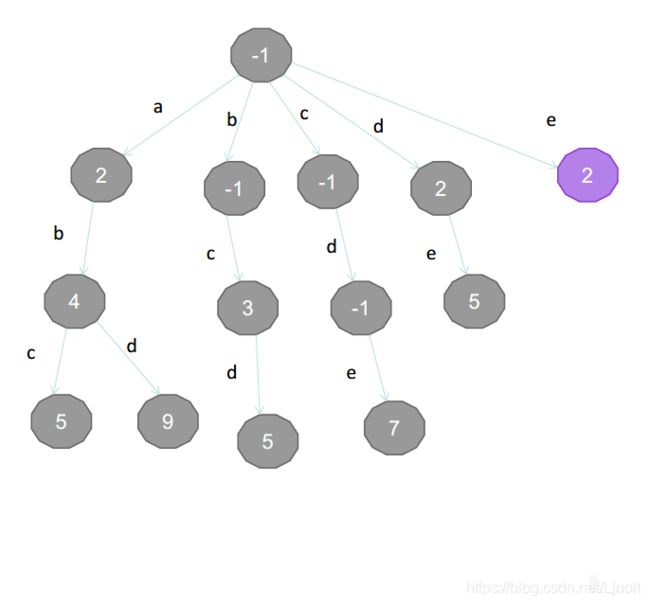
下面描述建树过程:

单词	分数
a	2
ab	4
abc	5
abd	9
bcd	5
bc	3
cde	7
de	5
d	2
e	2

‘











建树完成。

trie树的指针写法

struct dictree {
	dictree *child[26];
	int n; //根据需要变化
};

dictree *root;

例2 统计难题

HDU-1251
链接：http://acm.hdu.edu.cn/showproblem.php?pid=1251
https://vjudge.net/problem/HDU-1251

题目描述

Ignatius最近遇到一个难题,老师交给他很多单词(只有小写字母组成,不会有重复的单词出现),现在老师要他统计出以某个字符串为前缀的单词数量(单词本身也是自己的前缀).

输入描述

输入数据的第一部分是一张单词表,每行一个单词,单词的长度不超过10,它们代表的是老师交给Ignatius统计的单词,一个空行代表单词表的结束.第二部分是一连串的提问,每行一个提问,每个提问都是一个字符串.

注意:本题只有一组测试数据,处理到文件结束.

输出描述

对于每个提问,给出以该字符串为前缀的单词的数量.

样例输入

banana
band
bee
absolute
acm

ba
b
band
abc

样例输出

2
3
1
0

代码

注意：本题提交时选择的语言应为C++，不要选G++。选G++会内存超限的（不清楚原因）。
正常的写法：

#pragma GCC optimize(3,"Ofast","inline")
#pragma G++ optimize(3,"Ofast","inline")

#include 
#include 
#include 
#include 
#include 

#define R                  register int
#define re(i,a,b)          for(R i=a; i<=b; i++)
#define ms(i,a)            memset(a,i,sizeof(a))

using namespace std;

typedef long long ll;

int const N=1000005;

int tot=1;
int n[N];
int t[N][26];
char s[150];

void insert(char *s) {
    int k=0;
    for(int i=0; s[i]; i++) {
        int x=s[i]-'a';
        if(!t[k][x]) t[k][x]=tot++;
        k=t[k][x];
        n[k]++;
    }
}

int find(char *s) {
    int p=0;
    for(int i=0; s[i]; i++) {
        int x=s[i]-'a';
        if(t[p][x]) p=t[p][x];
            else return 0;
    }
    return n[p];
}

int main() {
    while(1) {
        gets(s);
        if(!strcmp(s,"")) break;
        insert(s);
    }
    while(scanf("%s",s)!=EOF) cout << find(s) << endl;
    return 0; 
}

指针的写法：

#pragma GCC optimize(3,"Ofast","inline")
#pragma G++ optimize(3,"Ofast","inline")

#include 
#include 
#include 
#include 
#include 

#define R                    register int
#define re(i,a,b)          for(R i=a; i<=b; i++)
#define ms(i,a)            memset(a,i,sizeof(a))

using namespace std;

typedef long long ll;

int const N=1000005;

struct dictree {
    struct dictree *child[26];
    int n;
};

struct dictree *root;

void insert(char *source) {
    int len,i,j;
    struct dictree *current,*newnode;
    len=strlen(source);
    if(len==0) return;
    current=root;
    for(i=0; i<len; i++) {
        if(current->child[source[i]-'a']!=0) {
            current=current->child[source[i]-'a'];
            current->n=current->n+1;
        } else {
            newnode=(struct dictree *)malloc(sizeof(struct dictree));
            for(j=0; j<26; j++) newnode->child[j]=0;
            current->child[source[i]-'a']=newnode;
            current=newnode;
            current->n=1;
        }
    }
}

int find(char *source) {
    int i,len;
    struct dictree *current;
    len=strlen(source);
    if(len==0) return 0;
    current=root;
    for(i=0;i<len;i++) {
        if(current->child[source[i]-'a']!=0) current=current->child[source[i]-'a'];
            else return 0;
    }
    return current->n;
}

int main() {
    char temp[11];
    int i,j;
    root=(struct dictree *)malloc(sizeof(struct dictree));
    for(i=0; i<26; i++) root->child[i]=0;
    root->n=2;
    while(gets(temp),strcmp(temp,"")!=0) insert(temp);
    while(scanf("%s",temp)!=EOF) {
        i=find(temp);
        printf("%d\n",i);
    }
}

例3 Remember the Word

LA-3942
链接：https://icpcarchive.ecs.baylor.edu/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=1943
https://vjudge.net/problem/UVALive-3942

题目大意

给定一个长度不超过300000的字符串str，然后给定n(n<=4000)个长度不超过100的字符串ai，问用ai组合成str有多少种方案数，最终结果mod 20071027。

思路

分析dp[i]表示(i到n)的串有几种表示方法。dp[i]=sigma(dp[j]) j>i 并且s[i…j-1]组成单词如果枚举j，判断是否组成单词，复杂度非常高。

我们可以把所有的单词组成trie树，然后只要在沿着trie树上去匹配就可以，最多找
100次(每个单词的最大长度是100)。

代码

#pragma GCC optimize(3,"Ofast","inline")
#pragma G++ optimize(3,"Ofast","inline")

#include 
#include 
#include 
#include 
#include 

#define R                  register int
#define re(i,a,b)          for(R i=a; i<=b; i++)
#define ms(i,a)            memset(a,i,sizeof(a))

using namespace std;

typedef long long ll;

int const N=300005;
int const MOD=20071027;

int len,n,tot;
int f[N],ed[N];
int tr[N][26];

char s[N],ts[1005];

void build(char *s) {
    int k=0;
    int len=strlen(s);
    for(int i=0; i<len; i++) {
        int id=s[i]-'a';
        if(tr[k][id]==0) tr[k][id]=++tot;
        k=tr[k][id];
    }
    ed[k]++;
}

void find(int x) {
    int k=0;
    for(int i=x; i<=len; i++) {
        int id=s[i]-'a';
        if(tr[k][id]==0) break;
        k=tr[k][id];
        if(ed[k]>0) f[x]=(f[x]+f[i+1])%MOD;
    }
}

int main() {
    int cas=0;
    while(scanf("%s",s+1)!=EOF) {
        len=0;
        for(int i=1; s[i]; i++,len++);
        scanf("%d",&n);
        memset(tr,0,sizeof(tr));
        memset(ed,0,sizeof(ed));
        tot=0;
        for(int i=0; i<n; i++) {
            scanf("%d",ts);
            build(ts);
        }
        memset(f,0,sizeof(f));
        f[len+1]=1;
        for(int i=len; i>=1; i--) {
            scanf("%s",ts);
            find(i);
        }
        printf("Case %d: %d\n",++cas,f[1]);
    }
    return 0;
}

例4 “strcmp()” Anyone?

UVA-11732
链接：https://onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=2832
https://vjudge.net/problem/UVA-11732

题目大意

int strcmp(char *s, char *t) 
{
	int i;
	for (i=0; s[i]==t[i]; i++) 
		if (s[i]=='\0')
			return 0;
	return s[i] - t[i];
}

如上所述，比较操作一直进行到两个字符串的对应位置处的字符不相同位置，比如than和that there 和the 各需要比较7次比较。

输入n个字符串串，两两调用一次strcmp,问总共要比较多次？

n<=4000,字符串长度不超过1000

思路

两两比较显然不现实，我们可以把单词一次插入到trie树里面，边插入，边计算。
由于最多可能会有4000*1000个字符，简单的二维数组表示法无能为力，只能采用左儿子，右兄弟的表示法。

代码

#pragma GCC optimize(3,"Ofast","inline")
#pragma G++ optimize(3,"Ofast","inline")

#include 
#include 
#include 
#include 
#include 

#define R                  register int
#define re(i,a,b)          for(R i=a; i<=b; i++)
#define ms(i,a)            memset(a,i,sizeof(a))

using namespace std;

typedef long long ll;

int const N=4000005;

struct Edge {
    int to,nt;
} e[N];

int tot,cnt,n;
int h[N],sum[N],ed[N];
ll ans;
char s[1005],z[N];

inline void add(int a,int b) {
    e[cnt].to=b;
    e[cnt].nt=h[a];
    h[a]=cnt++;
}

void build(char *s) {
    int k=0;
    for(int i=0; s[i]; i++) {
        int t=-1;
        for(int j=h[k]; j!=-1; j=e[j].nt) {
            int v=e[j].to;
            if(z[v]==s[i]) t=v;
        }
        if(t==-1) {
            add(k,++tot);
            t=tot;
            z[tot]=s[i];
        }
        if(k>0) ans=ans+(sum[k]<<1);
        ans=ans+sum[k]-sum[t];
        sum[k]++;
        k=t;
    }
    ans=ans+3*sum[k]+ed[k];
    sum[k]++;
    ed[k]++;
}

int main() {
    int cas=0;
    while(scanf("%d",&n)!=EOF && n>0) {
        cnt=tot=ans=0;
        memset(h,-1,sizeof(h));
        memset(sum,0,sizeof(sum));
        memset(ed,0,sizeof(ed));
        for(int i=0; i<n; i++) {
            scanf("%s",s);
            build(s);
        }
        printf("Case %d: %lld\n",++cas,ans);
    }
    return 0;
}

例5 最长公共前缀问题（模板题）

串的最长公共前缀（Longest Common Prefix，简称LCP）问题。

题目描述

给出N个小写英文字母串，以及Q个询问，即询问某两个串的最长公共前缀的长度是多少。

输入描述

第一行，两个数字N和Q；
接下来N行，每行一个字母串；接下来Q行，每行一个两个数字，表示对这两个编号的串进行询问。

输出描述

Q行，每行是对应问题的答案。

样例输入

2 2
abc
abd
1 1
1 2

样例输出

3
2

思路

明显的，两个串的最长公共前缀问题可以转换为trie树上的最近公共祖先问题。

1.利用并查集（Disjoint Set）采用经典的Tarjan 算法；

2.对于字母树上的每个结点，递推求出其所有向上2k后的祖先。查找两个点的最近公共祖先就可以通过它们同时快速地向上跳跃尽可能大的距离得到了。

其他练习

• POJ-1204
  链接：http://poj.org/problem?id=1204
  https://vjudge.net/problem/POJ-1204

• POJ-2001
  链接：http://poj.org/problem?id=2001
  https://vjudge.net/problem/POJ-2001

• POJ-3630
  链接：http://poj.org/problem?id=3630
  https://vjudge.net/problem/POJ-3630

• POJ-3690
  链接：http://poj.org/problem?id=3690
  https://vjudge.net/problem/POJ-3690

• HDU-2852
  链接：http://acm.hdu.edu.cn/showproblem.php?pid=2852
  https://vjudge.net/problem/HDU-2852