堆排序原理简记,及C++实现。
堆排序要用到完全二叉树的概念。完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当
其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。
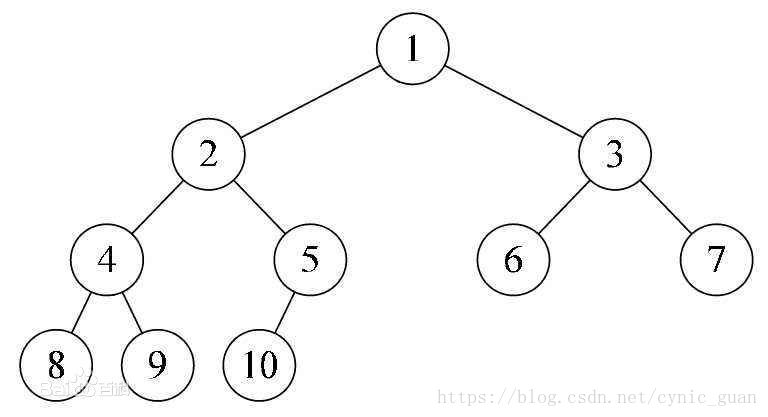
如上也为一个完全二叉树。
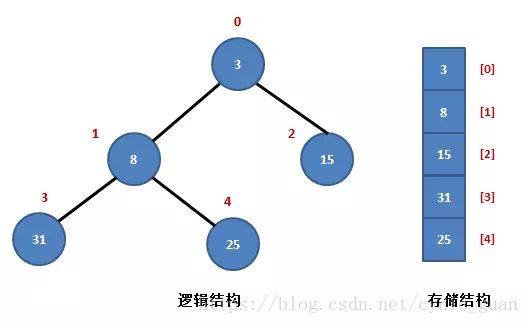
堆是一棵顺序存储的完全二叉树。
其中每个结点的关键字都不大于其孩子结点的关键字,这样的堆称为小根堆。
其中每个结点的关键字都不小于其孩子结点的关键字,这样的堆称为大根堆。
举例来说,对于n个元素的序列{R0, R1, … , Rn}当且仅当满足下列关系之一时,称之为堆:
(1) Ri <= R2i+1 且 Ri <= R2i+2 (小根堆)
(2) Ri >= R2i+1 且 Ri >= R2i+2 (大根堆)
其中i=1,2,…,n/2向下取整;
如上,左图为小根堆,虽然说是完全二叉树,但是其存储结构依然为如图所示的堆存储。
算法关键:
1.heapinsert()函数,在一个大根堆上插入一个数,使其形成新的大根堆。
2.heapify()函数,当某个Index位置的值更换时,重新让其变为大根堆。
算法流程:
1.用heapinsert()函数,将所输入数组arr[]变为大根堆形式。
2.将大根堆的根节点与arr[heapsize]交换,即将根节点移出该二叉树,并用heapify()使交换后的结构仍然为大根堆。
3.重复2操作。直到heapsize=1。
该过程即是通过大根堆的形式,不断将其最大值(根节点)放置在数组尾部,以达到排序目的。
算法复杂度:
1.heapinsert()部分,为log1+log2+“`+logN;故为O(N)的复杂度;
2.堆的存储表示是顺序的。因为堆所对应的二叉树为完全二叉树,而完全二叉树通常采用顺序存储方式。当想得到一个序列中第k个最小的元素之前的部分排序序列,最好采用堆排序。因为堆排序的时间复杂度是O(n+klog2n),若k≤n/log2n,则可得到的时间复杂度为O(n)。
C++代码如下。
此处仅为学习简记,若需详细请参考。其中有JAVA实现
https://mp.weixin.qq.com/s?__biz=MzI2NjA3NTc4Ng==&mid=2652080333&idx=1&sn=0940ed41b6ef55f36092c38dec914307&chksm=f1748328c6030a3e871e6ddc36cbf99c0b4732bae68c3fade35047c3fdcba3ff32cd35951de7&mpshare=1&scene=23&srcid=0824Ukb3ePyc4drFMJYP4sXV#rd
#include "stdafx.h"
#include;
using namespace std;
void heapinsert(int a[], int index)
{
while (a[index] > a[(index - 1) / 2])
{
swap(a[index], a[(index - 1) / 2]);
index = (index - 1) >> 1;
}
}
void heapify(int a[], int index, int heapsize)
{
int left = index * 2 + 1;
while (left < heapsize)
{
int largest = left + 1 < heapsize && a[left + 1] > a[left]
? left + 1 : left;
largest = a[largest] > a[index] ? largest : index;
if (largest == index) break;
swap(a[largest], a[index]);
index = largest;
left = index * 2 + 1;
}
}
void heapsort(int a[],int heapsize)
{
if (heapsize < 2) return;
for (int i = 0; i < heapsize; i++) {
heapinsert(a, i);
}
swap(a[0], a[--heapsize]);
while (heapsize > 0)
{
heapify(a, 0, heapsize);
swap(a[0], a[--heapsize]);
}
}
int main()
{
int as[] = {1,3,2,5,5,4,7,8,5};
int n = 9;
heapsort(as,n);
for (int i = 0; i < n; i++) cout << as[i] << endl;
}