进化策略算法
前言
进化策略 (Evolution Strategy) 后面都简称 ES,其本质就是:种群通过交叉产生后代,我们只保留较好的父代和子代,一直这样迭代下去,
我们的保留方式是:
父代产生后代,然后将后代DNA和原来的父母DNA合并,然后根据适应度排序,
然后选取前POP_SIZE的个体,重新组成一个种群
相关文章:
微生物进化算法(MGA)
遗传算法
前两个文章都是以长度大于1的列表当作DNA序列,
本次我们用实数来代替,即DNA就是一个实数,长度为1
遗传算法(GA)和进化策略(ES)的区别:
- 选好父母进行繁殖 (GA); 先繁殖, 选好的孩子 (ES)
- 通常用二进制编码 DNA (GA); 通常 DNA 就是实数, 比如 1.221 (ES)
- 通过随机让 1 变成 0 这样变异 DNA (GA); 通过
正态分布(Normal distribution)变异 DNA (ES)
传统的 GA 的 DNA 形式是这样:
DNA=11010010
而传统的 ES DNA 形式分两种, 它有两条 DNA. 一个 DNA 是控制数值的, 第二个 DNA 是控制这个数值的变异强度. 比如一个问题有4个变量. 那一个 DNA 中就有4个位置存放这4个变量的值 第二个 DNA 中就存放4个变量的变动幅度值.
DNA1=1.23, -0.13, 2.35, 112.5 可以理解为4个正态分布的4个平均值.
DNA2=0.1, 2.44, 5.112, 2.144 可以理解为4个正态分布的4个标准差.
所以这两条 DNA 都需要被 crossover(交叉) 和 mutate(变异).
基础进化策略
首先我们需要通过种群产生后代
首先的 make_kid 功能. 我们随机找到一对父母, 然后将父母的 DNA 和 mut_strength 基因都 crossover 给 kid. 然后再根据 mut_strength mutate 一下 kid 的 DNA. 也就是用正态分布抽一个 DNA sample. 而且 mut_strength 也能变异. 将变异强度变异以后, 他就能在快收敛的时候很自觉的逐渐减小变异强度, 方便收敛.
def make_kid(pop, n_kid):
"""
生成孩子
:param pop:
:param n_kid:
:return:
"""
# DNA
kids = {'DNA': np.empty((n_kid, DNA_SIZE))}
# 变异强度
kids['mut_strength'] = np.empty_like(kids['DNA'])
for kv, ks in zip(kids['DNA'], kids['mut_strength']):
# 随机从种群选取两个个体,一个父亲DNA,一个母亲DNA
p1, p2 = np.random.choice(np.arange(POP_SIZE), size=2, replace=False)
# 生成要变异的结点
cp = np.random.randint(0, 2, DNA_SIZE, dtype=np.bool_) # crossover points
# 将父DNA和母DNA交叉生成子DNA
kv[cp] = pop['DNA'][p1, cp]
kv[~cp] = pop['DNA'][p2, ~cp]
# 将父变异强度序列和母变异强度序列交叉生成子变异强度序列
ks[cp] = pop['mut_strength'][p1, cp]
ks[~cp] = pop['mut_strength'][p2, ~cp]
# 将变异强度也产生一定的变异
ks[:] = np.maximum(ks + (np.random.rand(*ks.shape)-0.5), 0.) # 实现将变异强度限制在非负数范围内
# 根据正态分布变异 mutate (change DNA based on normal distribution)
kv += ks * np.random.randn(*kv.shape) # 用于生成符合标准正态分布(均值为0,方差为1)的随机数,形状和kv的一样
# 将数组中的元素限制在一个指定的范围内 它将数组中小于指定最小值的元素替换为最小值,将大于指定最大值的元素替换为最大值
kv[:] = np.clip(kv, *DNA_BOUND) # clip the mutated value
return kids
之后我们将产生的后代和原来的种群合并,然后筛选重新组成一个种群
def kill_bad(pop, kids):
"""
将孩子DNA和原来的父母DNA合并,然后根据适应度排序,
然后选取前POP_SIZE的个体,重新组成一个种群
:param pop:
:param kids:
:return:
"""
# put pop and kids together
#将孩子DNA和原来的父母DNA合并
for key in ['DNA', 'mut_strength']:
pop[key] = np.vstack((pop[key], kids[key]))
# 获取适应度
fitness = get_fitness(F(pop['DNA'])) # calculate global fitness
# 然后根据适应度排序,然后选取前POP_SIZE的个体,重新组成一个种群
idx = np.arange(pop['DNA'].shape[0])
good_idx = idx[fitness.argsort()][-POP_SIZE:] # selected by fitness ranking (not value)
for key in ['DNA', 'mut_strength']:
pop[key] = pop[key][good_idx]
return pop
完整代码如下:
#!/usr/bin/env python
# -*- coding:utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
DNA_SIZE = 1 # DNA (real number) DNA大小
DNA_BOUND = [0, 5] # solution upper and lower bounds
N_GENERATIONS = 200
POP_SIZE = 100 # population size
N_KID = 50 # n kids per generation
def F(x): return np.sin(10*x)*x + np.cos(2*x)*x # to find the maximum of this function
def get_fitness(pred):
"""
返回适应度
:param pred:
:return:
"""
return pred.flatten() #将多维数组压平为一维数组。
def make_kid(pop, n_kid):
"""
生成孩子
:param pop:
:param n_kid:
:return:
"""
# DNA
kids = {'DNA': np.empty((n_kid, DNA_SIZE))}
# 变异强度
kids['mut_strength'] = np.empty_like(kids['DNA'])
for kv, ks in zip(kids['DNA'], kids['mut_strength']):
# 随机从种群选取两个个体,一个父亲DNA,一个母亲DNA
p1, p2 = np.random.choice(np.arange(POP_SIZE), size=2, replace=False)
# 生成要变异的结点
cp = np.random.randint(0, 2, DNA_SIZE, dtype=np.bool_) # crossover points
# 将父DNA和母DNA交叉生成子DNA
kv[cp] = pop['DNA'][p1, cp]
kv[~cp] = pop['DNA'][p2, ~cp]
# 将父变异强度序列和母变异强度序列交叉生成子变异强度序列
ks[cp] = pop['mut_strength'][p1, cp]
ks[~cp] = pop['mut_strength'][p2, ~cp]
# 将变异强度也产生一定的变异
ks[:] = np.maximum(ks + (np.random.rand(*ks.shape)-0.5), 0.) # 实现将变异强度限制在非负数范围内
# 根据正态分布变异 mutate (change DNA based on normal distribution)
kv += ks * np.random.randn(*kv.shape) # 用于生成符合标准正态分布(均值为0,方差为1)的随机数,形状和kv的一样
# 将数组中的元素限制在一个指定的范围内 它将数组中小于指定最小值的元素替换为最小值,将大于指定最大值的元素替换为最大值
kv[:] = np.clip(kv, *DNA_BOUND) # clip the mutated value
return kids
def kill_bad(pop, kids):
"""
将孩子DNA和原来的父母DNA合并,然后根据适应度排序,
然后选取前POP_SIZE的个体,重新组成一个种群
:param pop:
:param kids:
:return:
"""
# put pop and kids together
#将孩子DNA和原来的父母DNA合并
for key in ['DNA', 'mut_strength']:
pop[key] = np.vstack((pop[key], kids[key]))
# 获取适应度
fitness = get_fitness(F(pop['DNA'])) # calculate global fitness
# 然后根据适应度排序,然后选取前POP_SIZE的个体,重新组成一个种群
idx = np.arange(pop['DNA'].shape[0])
good_idx = idx[fitness.argsort()][-POP_SIZE:] # selected by fitness ranking (not value)
for key in ['DNA', 'mut_strength']:
pop[key] = pop[key][good_idx]
return pop
if __name__ == '__main__':
# 随机生成种群
# 这里直接用0-5的数字表示DNA,DNA长度为1
pop = dict(DNA=5 * np.random.rand(1, DNA_SIZE).repeat(POP_SIZE, axis=0), # initialize the pop DNA values
mut_strength=np.random.rand(POP_SIZE, DNA_SIZE)) # initialize the pop mutation strength values
plt.ion() # something about plotting
x = np.linspace(*DNA_BOUND, 200)
plt.plot(x, F(x))
for _ in range(N_GENERATIONS):
# something about plotting
if 'sca' in globals(): sca.remove()
sca = plt.scatter(pop['DNA'], F(pop['DNA']), s=200, lw=0, c='red', alpha=0.5);
plt.pause(0.05)
# 进化策略开始
kids = make_kid(pop, N_KID)
pop = kill_bad(pop, kids) # keep some good parent for elitism
plt.ioff()
plt.show()
(1+1)-ES进化策略
(1+1)-ES 总结如下:
- 有一个父代;
- 根据父代变异出一个子代;
- 在父代和子代中选好的那个变成下一代父代.
因此本算法不会像之前的算法有好多个体,这里只存在两个个体,适应度高的个体变异出子代,然后父代与子代相互竞争,根据优胜劣汰的法则,适应度高的当作父代。然后循环下去
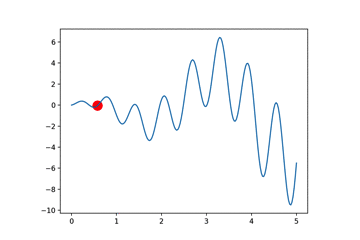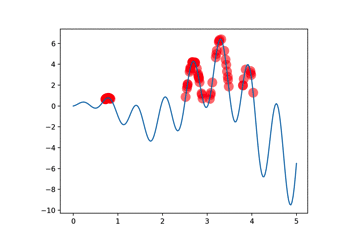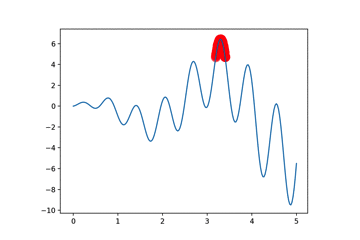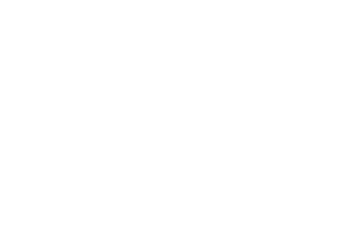
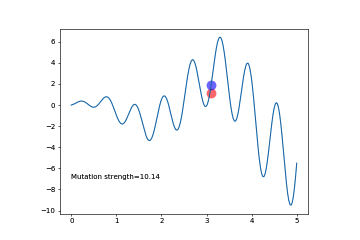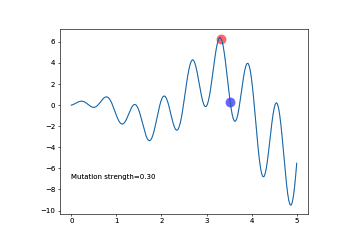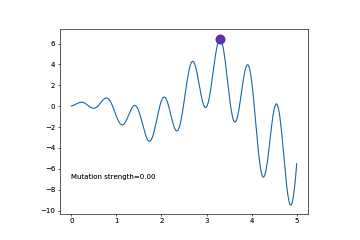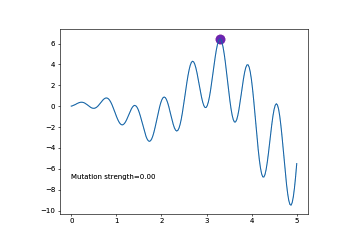
红点是父辈,当我比子代优秀的时候,我就一直在,子代受不了就自杀,当子代优于父辈的时候,父辈觉得很欣慰,便自己消失了,循环往复,直到某一代达到武林巅峰,在这个过程中,是什么决定了子代?实际上只有变异,因为我们的DNA实际上也只有横坐标。
这里只说与基础的进化策略的不同之处
首先是make_kid()函数,(1+1)-ES的make_kid()函数如下:
def make_kid(parent):
"""
产生子代的时候,不再进行交叉操作,只进行变异操作
:param parent:
:return:
"""
# 使用正态分布np.random.randn(DNA_SIZE)进行变异
k = parent + MUT_STRENGTH * np.random.randn(DNA_SIZE)
# 将k限制在0到5
k = np.clip(k, *DNA_BOUND)
return k
就是极简的两行代码,(1+1)-ES算法只进行了变异的操作,而不用进行交叉操作
其次我们的变异强度是动态改变的
在 kill_bad 中, 我们选择更为适合的, 不管是爸爸还是孩子, 只要是适合的就留下, 不适合的杀掉. 但是还有注意的一点是, 在这一步我们还要对 MUT_STRENGTH 进行一点改变. 改变的方法遵循了 1/5 successful rule. 这个方法是 ES 的开山鼻祖提出来的. 文献在这:
Rechenberg, I. 1973. Evolutionsstrategie – Optimierung technischer Systeme nach Prinzipien der biologischen Evolution, Frommann-Holzboog.
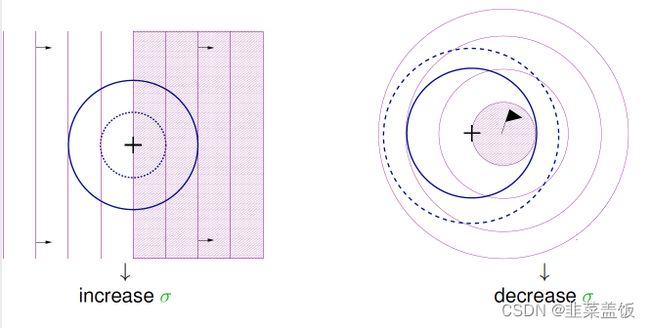
图中的意思是, 还没到收敛的时候(上面左图), 我们增大 MUT_STRENGTH, 如果已经快到收敛了(上右图), 我们就减小 MUT_STRENGTH. 那如何判断是否快到收敛没呢, 就是如果有1/5的变异比原始的 parent 好的话, 就是快收敛了(像上右图). 在上左图中, 有一半比原始 parent 好, 一半比较差, 所以还没到收敛. 在上面提到的课件中, 用一个公式就能概括这种1/5关系.
kill_bad()函数如下:
def kill_bad(parent, kid):
global MUT_STRENGTH
# 获取适应度
fp = get_fitness(F(parent))[0]
fk = get_fitness(F(kid))[0]
p_target = 1/5
# 如果父代适应度小于子代,就用子代去代替父代,否则保持不变
if fp < fk: # kid better than parent
parent = kid
ps = 1. # kid win -> ps = 1 (successful offspring)
else:
ps = 0.
# adjust global mutation strength
# 调整变异强度
MUT_STRENGTH *= np.exp(1/np.sqrt(DNA_SIZE+1) * (ps - p_target)/(1 - p_target))
return parent
完整代码如下:
#!/usr/bin/env python
# -*- coding:utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
DNA_SIZE = 1 # DNA (real number)
DNA_BOUND = [0, 5] # solution upper and lower bounds
N_GENERATIONS = 200
MUT_STRENGTH = 5. # initial step size (dynamic mutation strength)
def F(x): return np.sin(10*x)*x + np.cos(2*x)*x # to find the maximum of this function
# find non-zero fitness for selection
def get_fitness(pred): return pred.flatten()
def make_kid(parent):
"""
产生子代的时候,不再进行交叉操作,只进行变异操作
:param parent:
:return:
"""
# 使用正态分布np.random.randn(DNA_SIZE)进行变异
k = parent + MUT_STRENGTH * np.random.randn(DNA_SIZE)
# 将k限制在0到5
k = np.clip(k, *DNA_BOUND)
return k
def kill_bad(parent, kid):
global MUT_STRENGTH
# 获取适应度
fp = get_fitness(F(parent))[0]
fk = get_fitness(F(kid))[0]
p_target = 1/5
# 如果父代适应度小于子代,就用子代去代替父代,否则保持不变
if fp < fk: # kid better than parent
parent = kid
ps = 1. # kid win -> ps = 1 (successful offspring)
else:
ps = 0.
# adjust global mutation strength
# 调整变异强度
MUT_STRENGTH *= np.exp(1/np.sqrt(DNA_SIZE+1) * (ps - p_target)/(1 - p_target))
return parent
if __name__ == '__main__':
# 生成一个父代,本质上就是一个0-5的实数
parent = 5 * np.random.rand(DNA_SIZE) # parent DNA
plt.ion() # something about plotting
x = np.linspace(*DNA_BOUND, 200)
for _ in range(N_GENERATIONS):
# ES part
kid = make_kid(parent)
# 方便画图
py, ky = F(parent), F(kid) # for later plot
# 比较出一个适应度好的个体
parent = kill_bad(parent, kid)
# something about plotting
plt.cla()
plt.scatter(parent, py, s=200, lw=0, c='red', alpha=0.5, )
plt.scatter(kid, ky, s=200, lw=0, c='blue', alpha=0.5)
plt.text(0, -7, 'Mutation strength=%.2f' % MUT_STRENGTH)
plt.plot(x, F(x))
plt.pause(0.05)
plt.ioff()
plt.show()
参考:
莫烦Python
莫烦python之进化策略(1+1)-ES