Python实现三维空间中的RRT避障路径规划算法
文章目录
- 前言
- 一、算法原理
- 二、代码实现
-
- 1. 定义节点
- 2. 碰撞检测
- 3.RRT算法
- 4.完整代码
- 运行结果
前言
基于快速随机搜索树(Rapidly-exploring Random Tree, RRT)的优化算法,通过对状态空间中的采样点进行碰撞检测,避免了对空间的建模,能够有效地解决高维空间和复杂约束的路径规划问题,在机械臂路径规划与避障中扮演着关键角色。RRT算法通过随机生成的树状结构来探索高维空间,尤其适合于解决连续空间中的路径规划问题。
一、算法原理
RRT算法的基本思想是从起点出发,在状态空间中不断生成采样点,并检查这些点是否与环境中的障碍物相交。如果采样点位于无障碍区域,则将其作为树的一个新节点,并连接到树上最近的节点。这一过程反复进行,直到生成的节点触及目标区域,从而形成一条从起点到终点的路径。算法具体步骤网上介绍众多,可以详见:基于RRT优化算法的机械臂路径规划和避障matlab仿真, 文章中算法步骤部分如下:

二、代码实现
1. 定义节点
class Node3D:
def __init__(self, x, y, z, cost=0, parent=None):
self.x = x
self.y = y
self.z = z
self.cost = cost
self.parent = parent
def __str__(self):
return f'Node(x={self.x}, y={self.y}, z={self.z})'
2. 碰撞检测
def is_collision(nearest_node, new_node, obstacles):
for obstacle in obstacles:
nearest_node_xyz = np.array([nearest_node.x, nearest_node.y, nearest_node.z])
new_node_xyz = np.array([new_node.x, new_node.y, new_node.z])
v = nearest_node_xyz - new_node_xyz
p = np.array(obstacle[:3]) - nearest_node_xyz
a = np.dot(v, v)
b = 2 * np.dot(v, p)
c = np.dot(p, p) - obstacle[3] ** 2
disc = b ** 2 - 4 * a * c
if disc >= 0:
t1 = (-b + np.sqrt(disc)) / (2 * a)
t2 = (-b - np.sqrt(disc)) / (2 * a)
for t in [t1, t2]:
if 0 <= t <= 1:
return True
return False
3.RRT算法
class RRT3D:
def __init__(self, start, goal, bounds, obstacles, max_iter=10000, step_size=1.0):
self.start = Node3D(*start)
self.goal = Node3D(*goal)
self.bounds = bounds
self.step_size = step_size
self.goal_sample_rate = 0.1
self.obs = obstacles
self.max_iter = max_iter
self.start_tree = [self.start]
self.goal_tree = [self.goal]
self.path = None
def plan(self):
for i in range(self.max_iter):
start_rnd = self.get_random_node()
n_start_nearest = self.get_nearest_node(self.start_tree, start_rnd)
n_start_new = self.steer(n_start_nearest, start_rnd)
if n_start_new and not is_collision(n_start_nearest, n_start_new, self.obs):
self.start_tree.append(n_start_new)
if distance(self.goal, n_start_new) < self.step_size * 2:
self.get_path(n_start_new)
print(f'max iter num is:{i}')
print(f'node of start tree: {len(self.start_tree)}, node of goal tree: {len(self.goal_tree)}, '
f'start tree path node is:{len(self.path)}')
break
def get_random_node(self):
if np.random.rand() > self.goal_sample_rate:
position = np.array([np.random.uniform(b[0], b[1]) for b in self.bounds])
return Node3D(*position)
return self.goal
@staticmethod
def get_nearest_node(nodes, node):
min_dist = float("inf")
nearest = None
for n in nodes:
dist = distance(n, node)
if dist < min_dist:
min_dist = dist
nearest = n
return nearest
def steer(self, from_node, to_node):
new_node = Node3D(from_node.x, from_node.y, from_node.z)
diff_x = to_node.x - from_node.x
diff_y = to_node.y - from_node.y
diff_z = to_node.z - from_node.z
norm = np.sqrt(diff_x ** 2 + diff_y ** 2 + diff_z ** 2)
if norm > 0.0:
ratio = min(self.step_size, self.step_size / norm)
new_node.x += ratio * diff_x
new_node.y += ratio * diff_y
new_node.z += ratio * diff_z
new_node.cost = from_node.cost + distance(from_node, new_node)
new_node.parent = from_node
return new_node
def get_path(self, node):
self.path = [(self.goal.x, self.goal.y, self.goal.z)]
while node != self.start:
self.path.append((node.x, node.y, node.z))
node = node.parent
return self.path
def visualize(self, rrt):
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
for node in rrt.start_tree:
if node.parent is not None:
ax.plot([node.x, node.parent.x], [node.y, node.parent.y], [node.z, node.parent.z], 'r-')
for node in rrt.goal_tree:
if node.parent is not None:
ax.plot([node.x, node.parent.x], [node.y, node.parent.y], [node.z, node.parent.z], 'g-')
for obstacle in rrt.obs:
u, v = np.mgrid[0:2 * np.pi:20j, 0:np.pi:10j]
x = obstacle[0] + obstacle[3] * np.cos(u) * np.sin(v)
y = obstacle[1] + obstacle[3] * np.sin(u) * np.sin(v)
z = obstacle[2] + obstacle[3] * np.cos(v)
ax.plot_wireframe(x, y, z, color="gray")
if rrt.path:
path_x = [node[0] for node in rrt.path]
path_y = [node[1] for node in rrt.path]
path_z = [node[2] for node in rrt.path]
ax.plot(path_x, path_y, path_z, 'b-', label='Path')
ax.legend()
ax.set_xlabel('X axis')
ax.set_ylabel('Y axis')
ax.set_zlabel('Z axis')
plt.show()
4.完整代码
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
class Node3D:
def __init__(self, x, y, z, cost=0, parent=None):
self.x = x
self.y = y
self.z = z
self.cost = cost
self.parent = parent
def __str__(self):
return f'Node(x={self.x}, y={self.y}, z={self.z})'
def distance(node1, node2):
return np.linalg.norm(np.array([node2.x - node1.x, node2.y - node1.y, node2.z - node1.z]))
def is_collision(nearest_node, new_node, obstacles):
for obstacle in obstacles:
nearest_node_xyz = np.array([nearest_node.x, nearest_node.y, nearest_node.z])
new_node_xyz = np.array([new_node.x, new_node.y, new_node.z])
v = nearest_node_xyz - new_node_xyz
p = np.array(obstacle[:3]) - nearest_node_xyz
a = np.dot(v, v)
b = 2 * np.dot(v, p)
c = np.dot(p, p) - obstacle[3] ** 2
disc = b ** 2 - 4 * a * c
if disc >= 0:
t1 = (-b + np.sqrt(disc)) / (2 * a)
t2 = (-b - np.sqrt(disc)) / (2 * a)
for t in [t1, t2]:
if 0 <= t <= 1:
return True
return False
class RRT3D:
def __init__(self, start, goal, bounds, obstacles, max_iter=10000, step_size=1.0):
self.start = Node3D(*start)
self.goal = Node3D(*goal)
self.bounds = bounds
self.step_size = step_size
self.goal_sample_rate = 0.1
self.obs = obstacles
self.max_iter = max_iter
self.start_tree = [self.start]
self.goal_tree = [self.goal]
self.path = None
def plan(self):
for i in range(self.max_iter):
start_rnd = self.get_random_node()
n_start_nearest = self.get_nearest_node(self.start_tree, start_rnd)
n_start_new = self.steer(n_start_nearest, start_rnd)
if n_start_new and not is_collision(n_start_nearest, n_start_new, self.obs):
self.start_tree.append(n_start_new)
if distance(self.goal, n_start_new) < self.step_size * 2:
self.get_path(n_start_new)
print(f'max iter num is:{i}')
print(f'node of start tree: {len(self.start_tree)}, node of goal tree: {len(self.goal_tree)}, '
f'start tree path node is:{len(self.path)}')
break
def get_random_node(self):
if np.random.rand() > self.goal_sample_rate:
position = np.array([np.random.uniform(b[0], b[1]) for b in self.bounds])
return Node3D(*position)
return self.goal
@staticmethod
def get_nearest_node(nodes, node):
min_dist = float("inf")
nearest = None
for n in nodes:
dist = distance(n, node)
if dist < min_dist:
min_dist = dist
nearest = n
return nearest
def steer(self, from_node, to_node):
new_node = Node3D(from_node.x, from_node.y, from_node.z)
diff_x = to_node.x - from_node.x
diff_y = to_node.y - from_node.y
diff_z = to_node.z - from_node.z
norm = np.sqrt(diff_x ** 2 + diff_y ** 2 + diff_z ** 2)
if norm > 0.0:
ratio = min(self.step_size, self.step_size / norm)
new_node.x += ratio * diff_x
new_node.y += ratio * diff_y
new_node.z += ratio * diff_z
new_node.cost = from_node.cost + distance(from_node, new_node)
new_node.parent = from_node
return new_node
def get_path(self, node):
self.path = [(self.goal.x, self.goal.y, self.goal.z)]
while node != self.start:
self.path.append((node.x, node.y, node.z))
node = node.parent
return self.path
def visualize(self, rrt):
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
for node in rrt.start_tree:
if node.parent is not None:
ax.plot([node.x, node.parent.x], [node.y, node.parent.y], [node.z, node.parent.z], 'r-')
for node in rrt.goal_tree:
if node.parent is not None:
ax.plot([node.x, node.parent.x], [node.y, node.parent.y], [node.z, node.parent.z], 'g-')
for obstacle in rrt.obs:
u, v = np.mgrid[0:2 * np.pi:20j, 0:np.pi:10j]
x = obstacle[0] + obstacle[3] * np.cos(u) * np.sin(v)
y = obstacle[1] + obstacle[3] * np.sin(u) * np.sin(v)
z = obstacle[2] + obstacle[3] * np.cos(v)
ax.plot_wireframe(x, y, z, color="gray")
if rrt.path:
path_x = [node[0] for node in rrt.path]
path_y = [node[1] for node in rrt.path]
path_z = [node[2] for node in rrt.path]
ax.plot(path_x, path_y, path_z, 'b-', label='Path')
ax.legend()
ax.set_xlabel('X axis')
ax.set_ylabel('Y axis')
ax.set_zlabel('Z axis')
plt.show()
if __name__ == '__main__':
# 示例调用代码
start = (1.0, 1.0, 1.0)
goal = (49.0, 49.0, 49.0)
obstacles = [
(10, 30, 10, 8),
(35, 25, 40, 6),
(30, 10, 30, 10),
]
bounds = [(0, 50), (0, 50), (0, 50)]
iter_num, node_num = 0, 0
max_iter = 5
for i in range(max_iter):
rrt = RRT3D(start, goal, bounds, obstacles)
rrt.plan()
rrt.visualize(rrt)
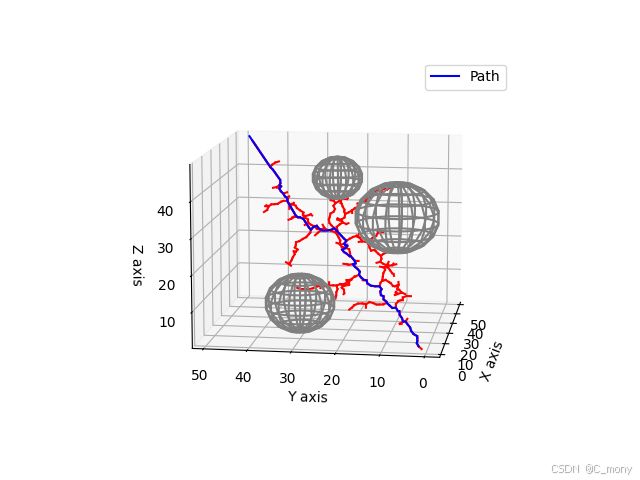
运行结果
运行上述代码5次的运行结果
max iter num is:405
node of start tree: 387, node number of path:100
max iter num is:451
node of start tree: 434, node number of path:98
max iter num is:356
node of start tree: 330, node number of path:96
max iter num is:318
node of start tree: 305, node number of path:98
max iter num is:455
node of start tree: 442, node number of path:103