2022李宏毅机器学习深度学习学习笔记第七周--局部最小点和鞍点

---

摘要

回顾了找出一个函式的三个步骤：先写一个带有未知参数的函式，定义一个可以判断参数好坏的loss，最后通过梯度下降法来优化参数使得loss的值变低；介绍任务攻略，说明在训练结果不好的时候，怎样进行分析，loss大的时候可能是bias和优化的问题，小的时候看测试数据的loss，测试数据的loss大可能是overfitting和mismatch的问题；最后讲了局部最小点和鞍点，在遇到临界点的时候可能optimization 会失败，以及通过数学方法判断是局部最小点还是鞍点。

---

一、怎么找一个函式（三步）

1.写一个带有未知参数的函式
先猜测函数f的数学式为y=b+wx1(y：预测的今天观看的人数，x1：昨天观看的人数，已知参数feature)，带有未知参数的函式叫model。
2.从训练资料中定义一个loss
loss是一个函式，输入为b,w,loss的输出代表了输入的b,w值的好坏。

具体过程：设L的参数为0.5k和1，将昨天的观看人数带入函式预测今天的人数，预测值与真实值的差记为e，依次算出每天的误差，loss的值为所有误差和的平均值，L越大参数越不好，L越小参数越好。

计算误差的方式有两种：MAE和MSE。
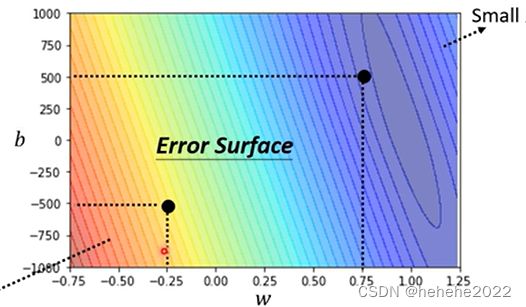
以下是真实数据的等高线图，越偏红色L越大，越偏蓝色L越小，w=1 b=250估测最精准。

3.最佳化的问题 Optimization
找到最好的一组w b，让loss的值最好。
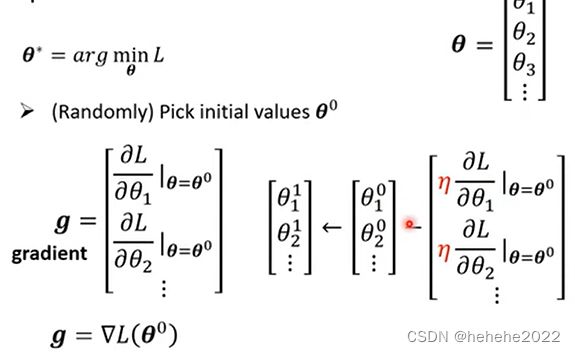
用到的优化方法叫做Gradient Descent 梯度下降法。
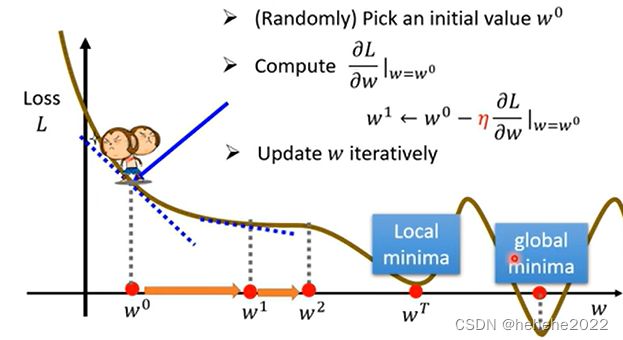
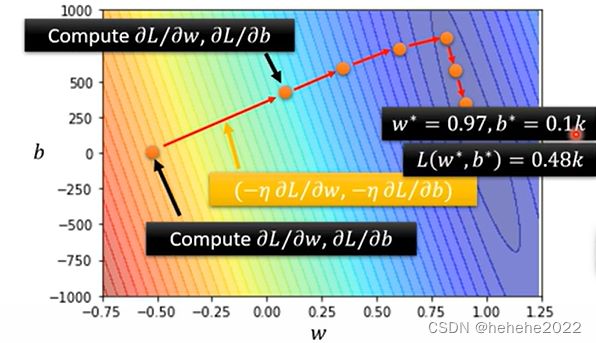
曲线为不同W得到的loss值，随机选取一个初始的点W0，计算在W0点W对L的微分（斜率），向使L降低的方向前进，前进步伐的大小取决于斜率和learning rate（学习率自己设定参数hyperparameters），新的位置为w1，反复进行以上操作，当微分的值为0的时候会停下来。

上面是找最好的w的过程，b也是类似的。进行这三个步骤的过程是训练（training）。

Sigmoid 函式

调整b(左右移动) w(改斜率) c(改高度) 制造不同的Sigmoid 函式。
新模型

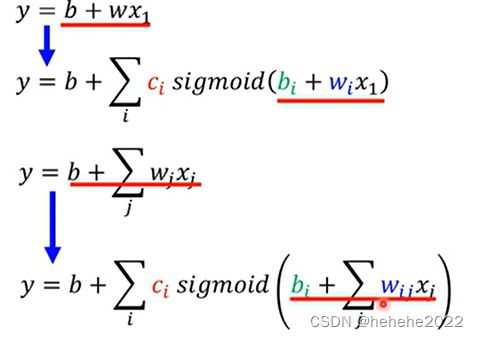
1.写一个带有未知参数的函式
2.定义loss
和之前的方法一样，给一组未知参数，计算预测值和真实值之间的差值，求loss。
3.优化

二、General Guide 任务攻略

如果对自己训练的结果不满意的话，先检查loss on training data，如果loss很大表示在训练资料上没有学好，可能是模型bias的问题，也可能时优化做的不好。

1.bias
模型太过简单，不同未知参数得到不同的函式，所有的函式集合成函式集，函式集中没有让loss变低的函式，即让loss变低的函式不在模型可以描述的范围内。这时重新设计model，比如增加feature（函式中的x），通过deep learning让他有更大的弹性。

2.optimization issue
梯度下降法找到loss低的函式，但不是函式集中最低的loss。

怎么区分是model bias还是optimization issue。

判断一些没有做过的问题，可以先跑一些比较浅的network，再训练一个深的模型，深的model弹性大但loss没办法压得更低，则是优化有问题。比如20层网络比50层网络在训练资料上的错误率还低，则是50层网络的optimization 没有做好。

如果是训练数据的loss很小，就看测试数据的loss；如果测试数据的loss也小，那就结束了，如果loss大那就可能是overfitting的问题，还可能是mismatch。

overfitting问题的解决，一是增加训练资料，二是Data augmentation 数据增强，用自己对这个问题的理解创造一些资料，三是不要让模型有大的弹性，限制model，比如定义函式为二次曲线，给定几个训练数据，函式曲线基本就固定了；限制model的方法有给少的未知参数、或者共用参数。mismatch是说训练资料和测试资料分布不一样，增加训练资料没有帮助。

三、局部最小点和鞍点

为什么optimization 会失败？

当gradient为0（统称为critical point）的时候，训练就停下来不会再更新参数了。但是不止是local minima（局部最小点）的情况gradient是0，还有saddle point（鞍点）。如果是卡在了local minima由于四周都是比较高的，没法再找到最低点，如果是saddle point，还是有路可以找到最低点。

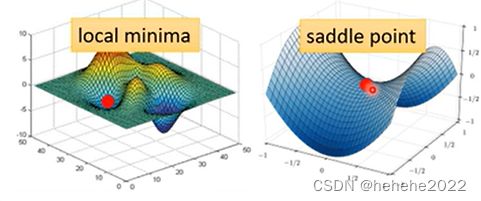
怎么区分到底是局部最小点还是鞍点？

要知道loss function的形状，给定一组参数，在这个参数附近的函式是能够被写出来的。
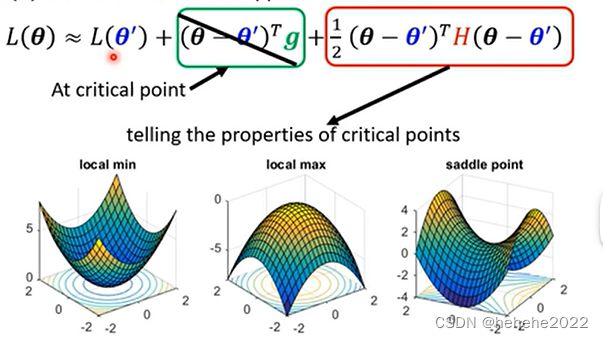
tayler series approximation泰勒级数展开

如果给定某一组参数,比如说上图去献中的蓝色的这个θ’，在其附近的loss function是有办法被写出来的,它写出来就是上图中的样子。
第一项的L（θ’）的含义就是当θ趋近于θ’的时候，L（θ）同时趋近于L（θ’）。

第二项是绿框g（g代表gradient）是一个向量，gradient来弥补θ跟θ’之间的差距。

第三项与Hessian Matrix（黑塞矩阵)有关,这里边有一个H，叫做Hessian，为一个矩阵。整个第三项在加上gradient后就真正抵消了L（θ’）与L（θ）之间的差距。H里是L的二次微分。

如果model训练到了一个critical point，意味gradient=0.也就是上图公式中绿色框这一项为零。此时g是一个zero vector（零向量），绿色的这一项完全都不见了，只剩下红色的这一项。

根据hessian判断θ’附近的地貌。

把（θ-θ’）用向量v来表示：

如果对任何可能的v，vᵀHv都大于零；也就是说现在θ无论为任何值，红色框里面都大于零，也就意味着L（θ）>L（θ’）。L（θ）不管值为多少，只要在θ’附近，L（θ）都大于L（θ’）。也就说明L（θ’）代表附近的一个最低点，所以它是local minima。

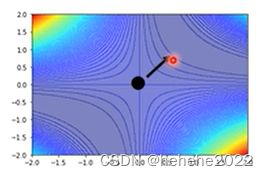
如果反过来说，对所有的v而言，vᵀHv都小于零，也就是红色框里面永远都小于零,也就是说θ无论为任何值，红色框里面都小于零。也就意味着L（θ）

第三个，假设vᵀHv有时候大于零，有时候小于零。你代入不同的v进去、代不同的θ进去，红色框里面有时候大于零，有时候小于零。意味着在θ’附近，有时候L(θ)>L(θ’)、有时候L(θ)

在线性代数中，如果对所有的v，vтHv都大于零，那这种矩阵叫做positive definite（正定矩阵），这类矩阵的所有的eigen value（特征值）都是正的。

所以如果算出一个hessian，直接看这个H的eigen value即可。

如果发现hessian metric的所有eigen value都是正的，即vᵀHv大于零，也就代表这是一个local minima。
反过来说也是一样。如何hessian metric的所有eigen value都是负的，即vᵀHv小于零，也就代表这是一个local maxima。

那如果eigen value有正有负，那就代表是saddle point。

​ 总的来说，只要算出hessian。它是一个矩阵，如果这个矩阵所有的eigen value都是正的，那就代表我们现在在local minima；如果它有正有负,就代表在saddle point。
举例：

一个network，它只有一个neuron（神经元），输入一个x，乘上w₁。而且这个neuron还没有activation function（激活函数），所以x乘上w₁以后就输出；然后再乘上w₂，之后再输出就得到最终的数据，也就是y。
假设没有bias，只有w₁ w₂两个参数，那我们可以穷举所有w₁跟w₂的数值，算出所有w₁ w₂数值所代来的loss，然后就画出error surface，如上图。
误差曲面的四个角落的loss是高的，上图中有一些critical point，也就是黑点的地方。

在以上的几个黑点中，原点这个地方的驻点是saddle point。因为以这个点为中心，往左上走loss会变大，往右下走loss会变大，往左下走loss会变小，往右下走loss会变小，因此它是一个saddle point。

而在误差曲面右上和左下的这两群critical point都是local minima。然后在原点有一个saddle point。这个是采用暴力方法，把所有的参数代入loss function以后画出的error surface。
直接算一个点是local minima还是saddle point的话有什么样的方法？
把loss的函式写出

在这个L中，ŷ（实际数值）减掉model（也就是w₁ w₂x）然后取square error（平方差）。把这一个loss function它的gradient求出来，w₁对L的微分,w₂对L的微分写出来是这个样子：

如果w₁=0 w₂=0就在圆心，并且w₁代0 w₂代0，w₁对L的微分 w₂对L的微分,算出来就都是零。这个时候就知道原点就是一个critical point，但它是local maxima、local minima还是saddle point就要看hessian才能够知道。


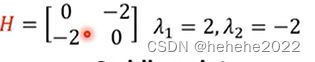
求出hessian，得到上面的矩阵，而特征值一正一副，所以是saddle point。
H知道了驻点的类型为鞍点，那么也可以通过H知道update的方向。

假设μ是H的eigen vector（特征向量）,λ是u的eigen value特征值。如果把vᵀHv中的v换成μ的话，因为μ是一个eigen vector，H乘上eigen vector（特征向量）等价于特征值乘特征向量，所以我们在这边得到μᵀ乘上λμ，然后再整理一下，把μᵀ跟μ乘起来,得到‖u‖²,所以得到λ‖u‖²。如果v代入的是一个eigen vector，也就是（θ-θ’）放的是一个eigen vector的话，会发现说红色框的项其实就是λ‖u‖²。当λ小于零时，也就是eigen value小于零的话，λ‖u‖²就会小于零，所以eigen value是负的,那λ‖u‖²这一整项就会是负的，也就是μ的转置乘上H乘上μ是负的,也就是上图的红色框里是负的。这意思就是说假设θ-θ’=μ，那你在θ’的位置加上μ，沿着μ的方向做update，也就是沿着特征向量的方向更新得到θ，你就可以让loss变小。
举例：
上面已经算出H的矩阵
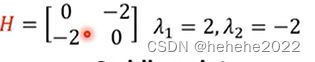发现这个Hessian有一个负的eigen value，为-2，取对应的eigen vector【1，1】，只要顺着这个eigen vector（也就是μ)的方向，去更新参数，就可以找到一个比saddle point的loss还要更低的点。

Saddle Point v.s. Local Minima
saddle point跟local minima谁比较常见呢？
从经验上看起来其实local minima并没有那么常见。多数时候训练到一个地方，gradient真的很小，然后参数不再update了，往往是因为卡在了一个saddle point。

相关的线性代数知识