图解:什么是最长递增子序列?
最长递增子序列
普通动态规划问题解题四步骤 (涉及最优子结构和重叠子问题)
基于状态压缩的动态规划解题步骤
0-1背包问题
在之前的文章中,我已经给大家介绍过了动态规划的常见类型、解题步骤,以及最重要的重叠子问题和最优子结构性质,从 0-1 背包问题开始,包括今日的最长递增子序列问题都可以视作刷题,找感觉,锻炼你的敏感性!
题目描述
[LeetCode 300] 给定一个无序的整数数组,找到其中最长上升子序列的长度。
输入输出示例:
输入: [10,9,2,5,3,7,101,18]
输出: 4
解释: 最长的上升子序列是 [2,3,7,101] 或 [2,5,7,18] 或 [2,3,7,101],它的长度是 4。
输入: [10,22,9,33,21,50,41,60,80]
输出: 6
解释: 最长的递增子序列为 [10,22,33,50,60,80]
输入: [3,5,2,8]
输出: 2
解释: 最长的递增子序列为 [3,5,8]
说明:
可能会有多种最长上升子序列的组合,你只需要输出对应的长度即可。你算法的时间复杂度应该为 。
进阶: 你能将算法的时间复杂度降低到 吗?
最长递增子序列(Longest Increasing Subsequence,LIS ),毫无疑问,可以使用动态规划进行求解,具体为何能够用动态规划求解,去看看 普通动态规划问题解题四步骤 这篇文章就是了!不过我这里也会解释奥!
首先从输入输出示例中,你应该注意到:
其一,最长递增子序列中元素并不要求连续,例如:[2,3,7,101] 中的元素在原序列中的元素 2 和 3 在原序列中并不紧挨;
其二,最长递增子序列的组合可能有多个,并不唯一,例如:[1,1,3,2] 的最长递增子序列为 [1,2] 或 [1,3];
其三,最长递增子序列中的「递增」是「严格递增」,例如:序列[1,1,3,2] 的最长递增子序列中无重复的元素 1,因为 [1,1,2] 不是严格递增
其四,最长递增子序列中元素的相对顺序必须保持和原始序列中的元素相对顺序一致,如下图所示:
此处暂停,回忆回忆动态规划的解题步骤,自己去力扣或者本地测一测,调一调!
方法一:递归
最优子结构:设 arr[0 ... n-1] 为输入数组,L(i) 表示以 arr[i] 为结尾的最长递增子序列的长度。
比如:输入 arr[] = {3, 5, 2, 8} ,L(0) 表示以 arr[0] = 3 结尾的最长递增子序列 3 的长度 1 ,L(0) = 1;L(1) 表示以 arr[1] = 5 结尾的最长递增子序列 {3,5} 的长度 2 ,L(1) = 2;L(2) 表示以 arr[2] = 2 结尾的最长递增子序列 {2} 的长度 1 ,即 L(2) = 1;L(3) 表示以 arr[3] = 8 结尾的最长递增子序列 {3,5,8} 的长度 3 ,即 L(3) = 3。
则 L(i) 可以被递归地表示为如下形式:
L(i) = 1 + max( L(j) ) ,其中 且 arr[j] < arr[i] ;比如 L(3) = 1 + L(1) = 3 .
或者 L(i) = 1 ,不存在 arr[j] < arr[i] 的情况;比如 L(2) = 1 ,因为 arr[0] 和 arr[1] 的值均大于 arr[2] 的值。
而最终一个给定数组的 LIS 就是取值最大的 max(L(i)) ,其中 ; 比如,对于数组 arr[] = {3,5,2,8} 而言,其 LIS 的长度为 L(3) = 3 。
由上面的分析可知,对于给定的数组 arr[], 以 arr[i] 结尾的最长递增子序列的长度等于子问题 arr[j] 的解加 1,其中 且 arr[j] < arr[i] 。也就是说最长递增子序列具有最优子结构性质,可以由子问题的解得到原问题的解。
一图胜千文,我们可以看一下递归树:
实现代码
class LIS
{
static int maxLIS; // 存储 max(f(i)) 0<=i maxEndingWithI){
maxEndingWithI = res + 1;
}
}
// 更新原数组最长递增子序列的长度
if (maxLIS < maxEndingWithI){
maxLIS = maxEndingWithI;
}
// 返回以 arr[n-1] 结尾的最长公共子序列的长度
return maxLIS;
}
// 包装递归函数
static int lis(int arr[], int n)
{
// 保存原数组的最长递增子序列的长度
maxLIS = 1;
// 调用递归函数
lisRecursion(arr, n);
return maxLIS;
}
}
复杂度分析
时间复杂度:如上面绘制的递归树一样,递归存在大量的重复子问题,耗费了大量的时间,时间复杂度为 量级。
空间复杂度: ,除递归调用使用的内部堆栈空间外,没有使用任何额外的外部空间。
方法二、动态规划
如上图所示,递归存在大量的子问题被重复计算,效率极低;可以通过备忘录或者 DP Table 对其进行剪枝,避免子问题的重复计算,从而提高算法的执行效率!
我们还是以数组 arr[] = {3, 5, 2, 8} 为例说明:
首先我们可以初始化 dp[] 中的元素均为 1,因为以数组 arr[] 中的任意一个元素结尾的最长递增子序列的长度至少为 1 (即自身,这就相当于假设数组仅包含一个元素,长度自然为 1,也是递归的出口):
假设你没有进行过递归的思考,现在直接进行 DP 解法的思考,也尚不知动态规划转移方程,那就耐心的一步一步分析!
当 i = 0 时,我们相当于仅考虑子数组 subarr[] = {3} 的情况,最长公共子序列的长度自然为 1:
当 i = 1 时,以 arr[1] = 5 结尾的子数组 subarr[] = {3,5} 的最长递增子序列为 {3,5} ,长度为 2,这似乎是显而易见的,但是考虑用子问题 dp[0] = 1 的解来得到当前问题的解 dp[1] = 2 又该如何得到呢?这就要回到问题本身,arr[1] = 5 ,只有当子问题的值 arr[0] = 3 小于时,才可以对其自身的长度加 1,而 arr[0] < arr[1] ,所以 dp[1] = max(dp[1],dp[0]+1) = 2 :
当 i = 2 时,arr[2] = 2 < arr[1] = 5 且 arr[2] < arr[0] ,所以不更新 dp[2] 的值:
当 i = 3 时,arr[0] = 3 < arr[3] = 8 ,则更新 dp[3] = max(dp[3],dp[0] + 1) = 2 ;
arr[1] = 5 < arr[3] = 8 ,则更新 dp[3] = max(dp[3],dp[1] + 1) = 3 ;
arr[2] = 2 < arr[3] = 8 ,则更新 dp[3] = max(dp[3],dp[2] + 1) = 3 ;
dp[i] 就表示以 arr[i] 结尾的最长递增子序列的长度,那么状态转移方程是什么呢?其实就是你一步一步总结的规律:
实现代码
class LIS
{
/* 动态规划解法 */
static int lis(int arr[],int n)
{
int dp[] = new int[n];
int i,j,max = 0;
/* 初始化 dp[] 数组中的每一个元素为 1 */
for ( i = 0; i < n; i++ ){
dp[i] = 1;
}
/* 自底向上计算每一个问题的最优解*/
for( i = 1; i < n; i++ ){
for( j = 0; j < i; j++ ){
if ( arr[i] > arr[j] && dp[i] < dp[j] + 1){
dp[i] = dp[j] + 1;
}
}
}
/* 遍历 dp 数组,找出最大值并返回 */
for( i = 0; i < n; i++ ){
if ( max < dp[i] ){
max = dp[i];
}
}
return max;
}
}
复杂度分析
时间复杂度:两层嵌套的 for 循环,外层为 n-1 次,内层最大为 n-2 次,时间复杂度为 量级
空间复杂度:
dp[]转态数组的大小与原数组arr[]相同,空间复杂度为 .
如果你回答到这里,面试官已经很满意了,但是你一定要再进一步,考虑一下如何将算法的时间复杂度降低到 呢?
方法三、动态规划 + 二分查找
从现在开始无需再考虑递归和 DP 解法,我们首先考虑一个简单的输入,然后动态添加元素,将其扩展到较复杂的输入。尽管这种方法可能很复杂,但是只要理解了其逻辑,编码就会很简单。
考虑初始的输入数组为 arr[] = {2,5,3} ,然后在随后的解释中不断扩展这个数组。
对于数组 arr[] = {2,5,3} 而言,LIS 为 {2,3} 或者 {2,5} 。同样,这里的递增还是严格递增的。
然后我们在原数组中添加两个元素, 7 和 11,即 arr[] = {2,5,3,7,11} 。此时数组的递增序列将进一步变长,即 {2,3,7,11} 与 {2,5,7,11} 。
紧接着,我们再向数组中添加一个元素 8 ,即 arr[] = {2,5,3,7,11,8} 。可以看到 8 比任意一个活动序列(active sequence,就是一个名字而已,可以动态生长的序列, {2,3,7,11} 与 {2,5,7,11} 就是活动序列)的最小元素都大。那么我们该如何用 8 来扩展现有递增序列呢?第一, 8 是否属于 LIS 中的元素?如果是,LIS 是什么样的呢?如果我们添加 8 ,其应该添加到 7 的后面(替换 11),即 {2,3,7,8} 与 {2,5,7,8} 。
由于我们现在模拟的是动态添加元素,动态更新数组的最长递增子序列,所以我们并不能确定添加 8 是否可以扩展 LIS 的长度。例如,假设 9 在输入数组中,即 arr[] = {2,5,3,7,11,8,7,9,...} ,我们就可以用 8 来替换 11, 因为潜在的元素 9 可以扩展新的序列 {2,3,7,8} 与 {2,5,7,8} 。
结论一: 假设最长递增序列最末尾的元素为 E ,我们可以在现存序列上添加(替换)当前元素 A[i] 的条件是:存在一个元素 A[j] ( ),使得 (添加) ,或者 (替换)。比如上面的例子中,最长递增序列 {2,3,7,11} 与 {2,5,7,11} 最末尾的元素 E = 11 ,当前决定是否添加(替换)的元素为 A[i] = 8 ,A[j] = 9 ,由于 ,所以将 11 替换为 8。(其实这就是各位大佬所说的贪心,如果已经得到的上升子序列结尾的数越小,遍历的时候后面接上一个数,就会有更大的可能性构成一个更长的上升子序列, 但是这样的贪心策略是有局限性的,接着向下看!)
在初始数组 arr[] = {2,5,3} 中,我们同样会碰到是否想递增序列 {2,5} 中添加元素 3 的问题,前面直接给出初始数组的两个最长递增子序列是为了解释的方便,但看到这里,我们其实可以用 3 替换序列 {2,5} 中的元素 5(因为 5 > 3 < 7),得到当前最长子序列 {2,3} 。
此时,你可能还是有些许疑惑,不妨耐心看完下文!
问自己一个问题:什么情况下在一个现有序列中添加或替换一个元素是合理的?
我们一起考虑另外一个简单的例子,初始的输入数组依然为 {2,5,3} ,但是 3 的下一个元素为 1,显然并不能扩展现有序列 {2,3} 或 {2,5} ,但是新的最下元素 1 有可能作为 LIS 的第一个元素,比如当数组为 arr[] = {2,5,3,1,2,3,4,5} 时,1 作为当前新的最长递增 {1,2,3,4,5} 的第一个元素。
结论二: 当我们在数组中遇到一个新的最小元素时,其可能是一个潜在的新序列的第一个元素。这就是仅考虑贪心策略会从一开始陷入局部最优的可能)。
基于上面两个结论,我们需要维护递增活动序列列表。
一般而言,我们有一个变长的活动序列列表集合。我们向列表中的所有活动序列添加一个元素 A[i] ,按照活动递增序列长度的降序扫描活动序列,并且检查所有活动序列最末尾的元素,找到最末尾元素小于 A[i] 的活动序列。
然后就是匹配下面三种情况:
情况一:如果 A[i] 比活动列表中所有活动序列最末尾的元素都小,我们将创建一个长度为 1 的新的活动序列,并删除其他等长的活动序列;
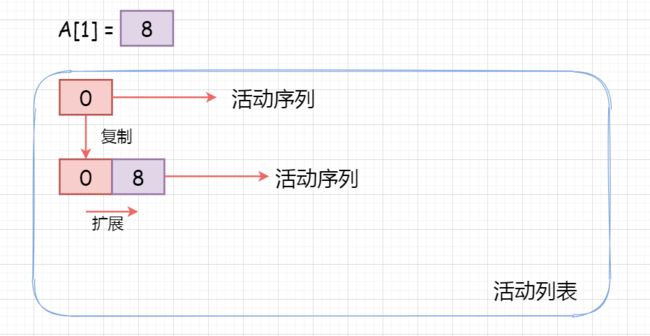
情况二:如果 A[i] 比活动列表中所有活动序列最末尾的元素都大,我们将复制最长的活动序列,并将 A[i] 添加进去;
情况三:如果 A[i] 介于中间,我们将找到一个最末尾元素比 A[i] 小的活动序列,复制并添加 A[i] 。并且将所有与添加新元素 A[i] 的活动序列等长的序列删除。
注意:在我们构造活动列表的时候,无论何时都遵循 “较短的活动序列最末尾的元素一定小于较长的活动序列最末尾的元素“。
我们用一个 wiki 上的例子 A[] = {0, 8, 4, 12, 2, 10, 6, 14, 1, 9, 5, 13, 3, 11, 7, 15} 一起来 “验算” 一遍即可。
A[0] = 0 ,情况一,当前活动列表为空,创建一个活动列表:
由于数组 A[] 太长,之后的图中就不画数组了,我们只关心当前要添加的元素即可。
A[1] = 8 ,情况二,复制并扩展:
A[2] = 4 ,情况三,复制、扩展 和 丢弃:
A[3] = 12 ,情况二,复制并扩展:
A[4] = 2 ,情况三,复制、扩展 和 丢弃:
之后的情况就直接给大家用一个长图表示了奥!
理解上面最长递增子序列的构造过程对于设计一个算法直观重要!很明显,最后得到活动列表满足 ”较短的活动序列最末尾的元素一定小于较长的活动序列最末尾的元素“ 的条件。你可以尝试对文章最开始的三个输入示例,按照上面的处理步骤自己操作一番,一定会对于你理解接下来的文章大有裨益,而且你会掌握的更牢固。
Tell me and I will forget. Show me and I will remember. Involve me and I will understand.(大学时候英语老师老说的一句话!)
PS:不妨拿出一副扑克牌,然后多洗几次扑克牌,随机抽出 10 张左右,按照上面的过程找出你抽出的扑克牌的最长递增子序列,这样一定会让你对 LIS 的理解和记忆帮助大大滴有!
在上面的整个过程中,你是否注意到,我们 所有的操作都是围绕活动序列最末尾的元素进行比较和操作的,我们可以把所有活动序列最末尾的元素存储在一个数组中,丢弃活动序列的操作就可以用替换数组中的元素模拟,扩展活动序列就相当于向数组中添加元素。
我们将使用一个辅助数组来存储最末尾的元素,这个数组的最大长度和输入数组一样长,当然也可能比输入数组的长度短。在最坏的情况下,数组被分割成 N 个大小为 1 的列表(注意,这并不会导致最坏的时间复杂度)。
丢弃一个元素,我们将在辅助数组中找到 A[i] 的位置(再次观察上面的活动列表的构造过程),并用A[i] 替换相应位置的值。通过向辅助数组中添加元素来扩展最长递增子序列,同时需要一个变量作为个计数器来保存辅助数组的长度。
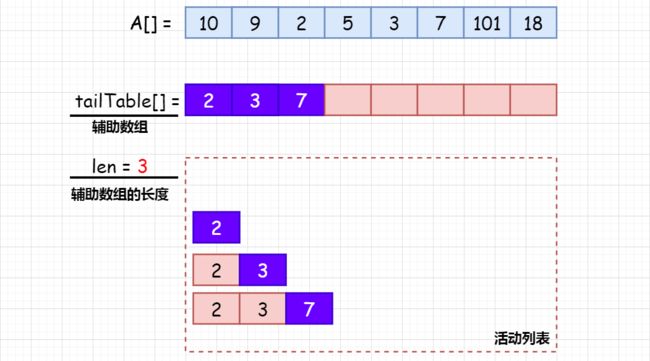
请不要介意,我可能还要重复一遍上面的操作,并且结合辅助数组和辅助数组的长度计数器再讲一个新的例子:A[] = [10,9,2,5,3,7,101,18] 。
如下图所示,先来简单的认识一下,我们涉及的存储变量,数组 A[] ,辅助数组 tailTable[] ,辅助数组的长度 len ,还有我们之前模拟的活动列表,当然接下来就是用辅助数组取代活动列表,为了让大家有一个清晰的认识和对应关系,我将两者放到了同一张图中:
第一步:用数组 A[0] 初始化辅助数组 tailTable ,即 tailTable[0] = A[0] ,len = 1 ,活动列表相应的添加 A[0] :
第二步:添加 A[1] = 9 ,情况一,添加元素 A[1] 小于当前活动列表中所有活动序列最末尾的元素,则创建一个长度为 1 的新的活动序列,并删除其他等长的活动序列。对应到辅助数组,该如何做到这一件事情呢?辅助数组 tailTable[] 本身存储的就是活动序列最末尾的元素,要比较大小,直接用 A[1] 和辅助数组 tailTable[] 中的元素比较不就可以了?发现当前辅助数组中就一个元素,且大于添加元素 A[1] ,直接替换不就可以了?
第三步,添加元素 A[2] = 2 ,这就和第二步一样吗?
第四步:添加元素 A[3] = 5 ,情况二,添加元素 A[3] 大于所有活动序列最末尾的元素,相应的直接和辅助数组最末尾的元素比较大小即可判断是否是情况二,如果是直接在辅助数组中添加元素 A[3]:
第五步:添加元素 A[4] = 3 ,情况三, 2 < A[4] < 5,复制 2 → 添加 3 → 丢弃等长的;对应到辅助数组,首先如何确定 A[4] 应该添加在谁的后面呢,也就是 A[4] 的位置?我们使用二分查找法,关于二分查找我之前已经有分享过了,可以看 二分查找就该这样学 这篇文章,确定之后替换比其大的元素 5 即可,如下所示:
第六步:添加元素 A[5] = 7 , 情况二,直接在辅助数组中添加元素 A[5] = 7 ,活动列表的相应变化如图所示,注意活动列表中的元素和辅助数组中的元素:
第七步:添加元素 A[6] = 101 ,情况二,直接在辅助数组中添加 A[6] = 101 :
第八步:添加元素 A[7] = 18 ,情况三,用二分查找法在辅助数组 tailTable 中找位置,然后替换相应的元素:
这就是 算法的由来,我想你也理解了,不过这里给大家再次提个醒,辅助数组中的元素是活动列表中所有活动序列最末尾的元素,而不是我们要求的最长递增子序列。
举个简单的例子,上面的第八步是添加元素 A[7] = 18 ,现在我们将其改成 A[7] = 4 进行添加效果会如何呢?依旧是情况三,但是此时的 3 < 4 < 7 ,我们将会把辅助数组中的 7 替换为 4,活动列表则是复制 [2,3] → 添加 4 → 删除等长的 [2,3,7] :
但是可以确定的是,最长递增子序列的长度是和辅助数组的长度相同的,所有最后返回 len 即可。
实现代码
不妨先自己写写二分查找,然后根据上面的讲解自己调一调代码,其实理解了思想,实现代码相当简单!
class LIS {
// 二分查找
static int CeilIndex(int tail[], int left, int right, int key)
{
while (right - left > 1) {
int mid = left + (right - l) / 2;
if (tail[mid] >= key){
right = mid;
}
else{
left = mid;
}
}
return right;
}
static int lengthOfLIS(int A[], int n)
{
// 创建一个大小为 n 的辅助数组
int[] tailTable = new int[n];
int len; // 存储辅助数组的元素个数
//边界情况,将数组中的第一个元素直接添加进去
tailTable[0] = A[0];
len = 1; //长度加 1
for (int i = 1; i < n; i++) {
// 新的最小值,情况一
if (A[i] < tailTable[0])
{
tailTable[0] = A[i];
}
else if (A[i] > tailTable[len - 1]){
// A[i] 为最大值,情况二
tailTable[len++] = A[i];
}
else{ // 情况三,找到 A[i] 在 tailTable 的位置并替换
tailTable[CeilIndex(tailTable, -1, len - 1, A[i])] = A[i];
}
}
return len;
}
public static void main(String[] args)
{
int A[] = {10,9,2,5,3,7,101,18};
System.out.println("Length of Longest Increasing Subsequence is: " + lengthOfLIS(A, A.length));
}
}
复杂度分析
时间复杂度:外层循环的大小为 ,内层的
else语句中的二分查找在最坏的情况下时间复杂度为 ,【你可以考虑一下最坏情况,或者一种输入样例,欢迎评论区留言,说出你心中的例子,可能有惊喜奥!】所有总的时间复杂度为 量级。空间复杂度: 。
感谢各位小伙伴能读到这里,最后再给大家布置个小作业,你能否实现一个输出给定数组最长递增子序列的代码呢?
比如输入:A[] = [ 2, 5, 3, 7, 11, 8, 10, 13, 6] ,输出为:[2,3,7,8,10,13] 。
一定要自己思考奥!做完了后台回复 【 LIS 】可以获取景禹的参考版本!记得三连,原创不易!
推荐阅读:
动态规划之武林秘籍(普通DP 方法论)
这才是真正的状态压缩动态规划好不好!!!(状压 DP 方法论)
作者:景禹,一个追求极致的共享主义者,想带你一起拥有更美好的生活,化作你的一把伞。