最长公共子序列和最长公共子串的动态规划实现(java)
一,基础概念
1,什么是子序列?
将给定序列中零个或多个元素(如字符)去掉后所得结果。
例如:给定序列【A,B,C,D,E,F,G,H】
子序列:A,C,E,F
同理,【A,H】,【C,D,E】等都是子序列
2,什么是子串?
给定序列中零个或多个连续的元素(如字符)组成的子序列。
例如:给定序列【A,B,C,D,E,F,G,H】
子序列:C,D,E,F
同理,【C,D,E,F】,【G,H】等都是子串
这里就能明显看出区别,子序列可以不连续,而子串连续。
3,什么是最长公共子序列?
最长公共子序列(LCS)是一个在一个序列集合中(通常为两个序列)用来查找所有序列中最长子序列的问题。一个数列 ,如果分别是两个或多个已知数列的子序列,且是所有符合此条件序列中最长的,则称为已知序列的最长公共子序列。
4,什么是最长公共子串?
最长公共子串问题是寻找两个或多个已知字符串最长的子串。此问题与最长公共子序列问题的区别在于子序列不必是连续的,而子串却必须是。
二,求解方案
最长公共子序列
1,原理
动态规划的一个计算两个序列的最长公共子序列的方法如下:
以两个序列 X、Y 为例子:
设有二维数组f[i,j] 表示 X 的 i 位和 Y 的 j 位之前的最长公共子序列的长度,则有:
f[1][1] = same(1,1);
f[i,j] = max{f[i-1][j -1] + same(i,j),f[i-1,j],f[i,j-1]};
其中,same(a,b)当 X 的第 a 位与 Y 的第 b 位相同时为“1”,否则为“0”。
此时,二维数组中最大的数便是 X 和 Y 的最长公共子序列的长度,依据该数组回溯,便可找出最长公共子序列。
该算法的空间、时间复杂度均为O(n^2),经过优化后,空间复杂度可为O(n)。
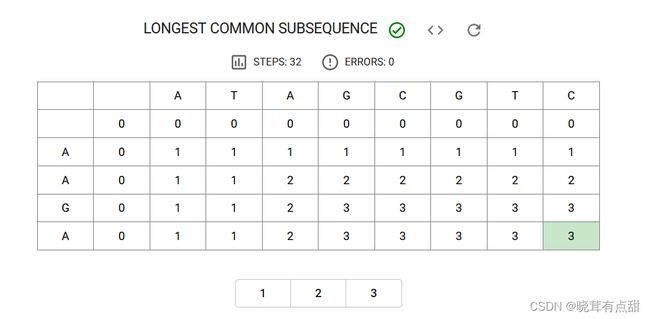
下面列出动态规划的表格:
i和j等于0时也就是第一行和第一列,由于没有元素,所以最长公共子序列也没有。
接下来i从第二行的第二个元素开始,如果两个元素相同,就在c[i-1][j-1]的基础上加1,这是第一种情况。
如果两个元素不同,就将c[i-1,j]和c[i,j-1]中最大的一个记录下去,这是第二种情况。
这里可以参考一下这个视频中的讲解步骤,感谢up主!!
最长公共子序列 - 动态规划 Longest Common Subsequence![]() https://www.bilibili.com/video/BV14A411v7mP?spm_id_from=333.337.search-card.all.click
https://www.bilibili.com/video/BV14A411v7mP?spm_id_from=333.337.search-card.all.click
这里在推荐一个可以练习该算法的动态规划表格的网站,可以模拟动态规划的过程,建议多练习几遍:最长公共子序列动态规划算法练习![]() https://alchemist-al.com/algorithms/longest-common-subsequence
https://alchemist-al.com/algorithms/longest-common-subsequence
由此,我们就有了动态规划的递推方程式:
有了递推方程式后,我们还需要一个Rec[ i ][ j ]数组来记录c数组的值是由哪一个子问题的解得到的,这在构造最长公共子序列的时候会用到。下面列出递推的图解步骤:
这里要注意,如果Rec等于1时要输出x[i-1],因为Rec的行和列在定义的时候比x这个数组要多一个单位,我们从上图中就能看出。
2,代码
public class Lcs{
public void LcsLength(char[] x,char[] y,int[][] Rec){
//初始化
int [][]c=new int[x.length+1][y.length+1];
for(int i=0;i<=x.length;i++){
c[i][0]=0;
Rec[i][0]=0;
}
for(int j=0;j<=y.length;j++){
c[0][j]=0;
Rec[0][j]=0;
}
//动态规划
for(int i=1;i<=x.length;i++){
for(int j=1;j<=y.length;j++){
if(x[i-1]==y[j-1]){
c[i][j]=c[i-1][j-1]+1;
//当Rec为1时,表示Xi和Yi的最长公共子序列是由Xi-1和Yi-1的最长公共子序列在尾部加上Xi所得的子序列。
Rec[i][j]=1;
}else if(c[i-1][j]>=c[i][j-1]){
c[i][j]=c[i-1][j];
//当Rec为2时,表示Xi和Yi的最长公共子序列与Xi-1和Yi的最长公共子序列相同。
Rec[i][j]=2;
}else{
c[i][j]=c[i][j-1];
//当Rec为3时,表示Xi和Yi的最长公共子序列与Xi和Yi-1的最长公共子序列相同。
Rec[i][j]=3;
}
}
}
System.out.println("动态规划表格为:");
for(int i=0;i<=x.length;i++){
for(int j=0;j<=y.length;j++){
System.out.print(c[i][j]+" ");
}
System.out.print("\n");
}
System.out.println("记录子问题解的来源的数组为:");
for(int i=0;i<=x.length;i++){
for(int j=0;j<=y.length;j++){
System.out.print(Rec[i][j]+" ");
}
System.out.print("\n");
}
System.out.println("最长公共子序列为:");
lcs(x.length,y.length,x,Rec);
}
public void lcs(int i,int j,char[] x,int[][] Rec){
if(i==0||j==0) return ;
if(Rec[i][j]==1){
lcs(i-1,j-1,x,Rec);
System.out.print(x[i-1]);
}else if(Rec[i][j]==2) lcs(i-1,j,x,Rec);
else lcs(i,j-1,x,Rec);
}
public static void main(String[] args) {
Lcs object=new Lcs();
char[] x={'A','A','G','A'};
char[] y={'A','T','A','G','C','G','T','C'};
//定义一个数组用来记录c[i][j]的值是由哪一个子问题的解得到的
int [][] Rec=new int[x.length+1][y.length+1];
object.LcsLength(x,y,Rec);
}
}最长公共子串
1,原理
最长公共子串要求子序列是连续的,我们可以在最长公共子序列的基础上对递推关系式进行修改,因此这里我们依旧使用c[i][j]来表示表示 X 的 i 位和 Y 的 j 位之前的最长公共子序列的长度,也就是动态规划的二维表。
大致思路如下:
第一种情况if 两个数组中的元素相同,那么就在c[i-1][j-1]的基础上加1;
第二种情况if 两个数组中的元素不同,那么就让c[i][j]=0;
同时,为了输出最长公共子串的元素,我们需要借助两个变量对最大长度以及最大长度的停止下标进行记录,分别借助result,flag。这里需要在第一种情况if时进行递推,在循环中以此将数组中最大的数赋值给result,并用flag来记录此时的行/列字符串的下标,后续可以进行遍历。(后续用行用列都可以,我这里使用了列,也就是x数组来回溯元素)
递推关系式如下:
if(x[i]=y[j]) c[i][j]=c[i-1][j-1]+1;
else c[i][j]=0;
这里依旧可以通过这个网站进行练习最长公共子串动态规划练习![]() https://alchemist-al.com/algorithms/longest-common-substring
https://alchemist-al.com/algorithms/longest-common-substring
2,代码
public class Lcs2 {
public void GetLcs(char[] x,char[] y) {
//初始化
int[][] c = new int[x.length + 1][y.length + 1];
for (int i = 0; i <= x.length; i++) {
c[i][0] = 0;
}
for (int j = 0; j <= y.length; j++) {
c[0][j] = 0;
}
//动态规划
int result=0,flag=0;
for(int i=1;i<=x.length;i++){
for(int j=1;j<=y.length;j++){
if(x[i-1]==y[j-1]){
c[i][j]=c[i-1][j-1]+1;
result=Math.max(c[i][j],result);
flag=j;
}else{
c[i][j]=0;
}
}
}
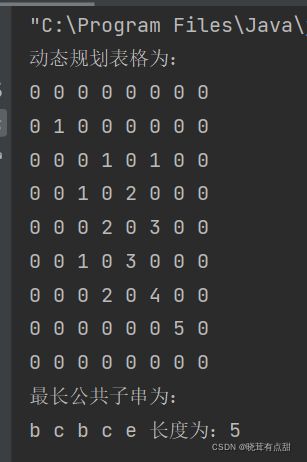
System.out.println("动态规划表格为:");
for(int i=0;i<=x.length;i++){
for(int j=0;j<=y.length;j++){
System.out.print(c[i][j]+" ");
}
System.out.print("\n");
}
System.out.println("最长公共子串为:");
lcs(flag,result,x);
System.out.println("长度为:"+result);
}
public void lcs(int flag,int result,char[] x){
if(flag==0||result==0)
return;
for(int i=flag-result+1;i<=flag;i++){
System.out.print(x[i]+" ");
}
}
public static void main(String[] args) {
Lcs2 solution=new Lcs2();
char[] x={'a','c','b','c','b','c','e','f'};
char[] y={'a','b','c','b','c','e','d'};
solution.GetLcs(x,y);
}
}三,总结
最长公共子序列的难度较子串高些,主要在回溯时,需要通过递归来找到动态规划的入口,或者说具体步骤。而最长公共子串只需要我们进行一步标记,后续通过标记就可以直接输出了。我觉得这个不同点就出现在子序列连续和不连续这个点上,不连续的话我们就没法直接去标记数组位置,只能通过具体步骤来回溯,动态规划本身在实现这个问题上并不困难。
有任何问题还请评论区指正,谢谢!