动态规划DP
动态规划
- 基础类DP
-
- leetcode70. 爬楼梯
- leetcode746. 使用最小花费爬楼梯
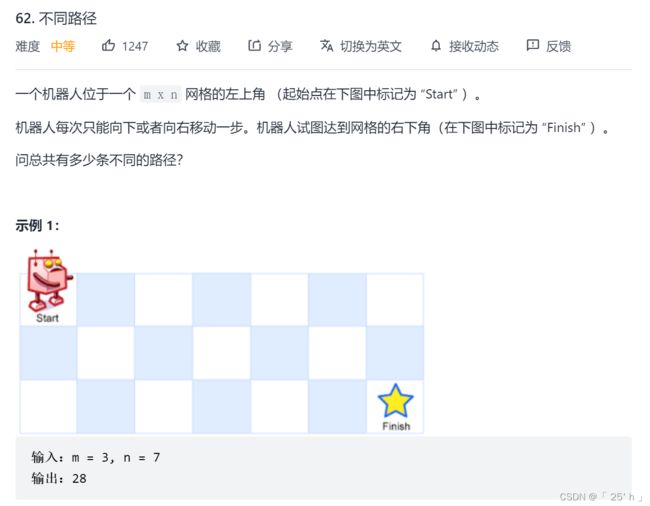
- leetcode62. 不同路径
- leetcode63. 不同路径 II
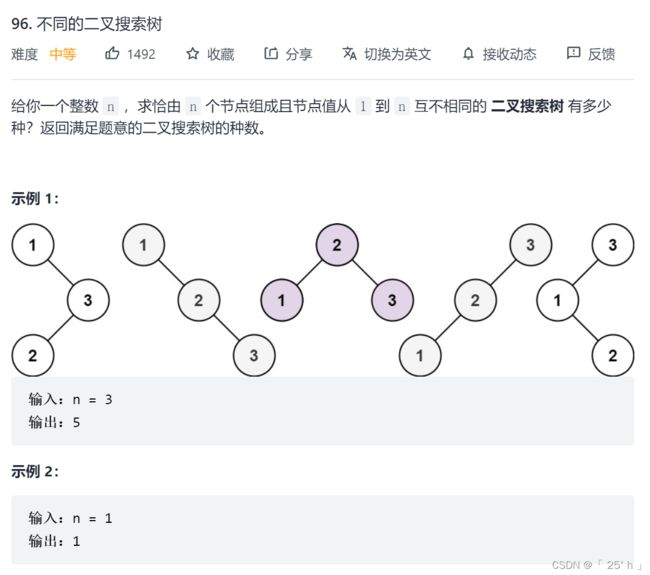
- leetcode96. 不同的二叉搜索树
- leetcode64最小路径和
- leetcode329. 矩阵中的最长递增路径
- 01背包类DP
-
- leetcode416. 分割等和子集
- leetcode1049. 最后一块石头的重量 II
- leetcode494. 目标和
- leetcode474. 一和零
- 完全背包
-
- leetcode518. 零钱兑换 II
- leetcode377. 组合总和 Ⅳ
- leetcode70爬楼梯(续集)
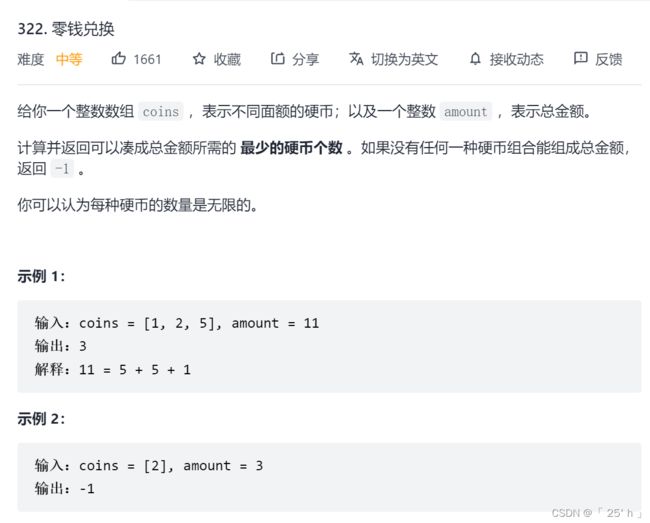
- leetcode322. 零钱兑换
- leetcode279. 完全平方数
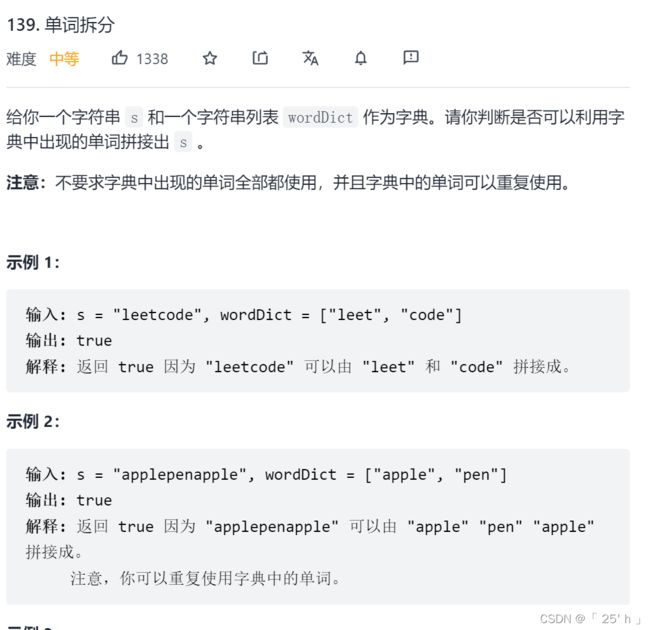
- leetcode139. 单词拆分
- 打家劫舍
-
- leetcode198. 打家劫舍
- leetcode213. 打家劫舍 II
- leetcode337打家劫舍 III
- leetcode740. 删除并获得点数
- 股票问题
-
- leetcode121. 买卖股票的最佳时机
- leetcode122. 买卖股票的最佳时机 II
- leetcode714. 买卖股票的最佳时机含手续费
- leetcode123. 买卖股票的最佳时机 III
- leetcode188. 买卖股票的最佳时机 IV
- leetcode309. 最佳买卖股票时机含冷冻期
- 序列问题
-
- leetcode300. 最长递增子序列
- leetcode354. 俄罗斯套娃信封问题
- leetcode1143. 最长公共子序列
- leetcode583. 两个字符串的删除操作
- leetcode1035. 不相交的线
- leetcode718. 最长重复子数组
- leetcode115. 不同的子序列
- leetcode72. 编辑距离
- leetcode647. 回文子串
- leetcode516. 最长回文子序列
- leetcode5. 最长回文子串
基础类DP
leetcode70. 爬楼梯
- 经典动态规划
class Solution {
public int climbStairs(int n) {
int[] dp = new int[n + 2];
dp[n + 1] = 1;
dp[n] = 1;
for (int i = n - 1; i >= 1; i--) {
dp[i] = dp[i + 1] + dp[i + 2];
}
return dp[1];
}
}
- 空间压缩(测试的有问题。。。。)
class Solution {
public int climbStairs(int n) {
int a = 1, b = 1;
int res = 0;
for (int i = n - 1; i >= 0; i--) {
res = a + b;
a = b;
b = res;
}
return res;
}
}
leetcode746. 使用最小花费爬楼梯
class Solution {
public int minCostClimbingStairs(int[] cost) {
int[] dp = new int[cost.length + 1];
dp[cost.length] = 0;
dp[cost.length - 1] = cost[cost.length - 1];
for (int i = cost.length - 2; i >= 0; i--) {
dp[i] = Math.min(dp[i + 1], dp[i + 2]) + cost[i];
}
return Math.min(dp[0], dp[1]);
}
}
- 空间压缩
class Solution {
public int minCostClimbingStairs(int[] cost) {
int a = 0, b = cost[cost.length - 1], res = 0;
for (int i = cost.length - 2; i >= 0; i--) {
res = Math.min(a, b) + cost[i];
a = b;
b = res;
}
return Math.min(a,b);
}
}
leetcode62. 不同路径
class Solution {
public int uniquePaths(int m, int n) {
int[][] dp = new int[m][n];
for (int i = 0; i < m; i++) {
dp[i][n - 1] = 1;
}
for (int i = 0; i < n; i++) {
dp[m - 1][i] = 1;
}
for (int i = m - 2; i >= 0; i--) {
for (int j = n - 2; j >= 0; j--) {
dp[i][j] = dp[i][j + 1] + dp[i + 1][j];
}
}
return dp[0][0];
}
}
- 空间压缩
class Solution {
public int uniquePaths(int m, int n) {
int[] dp = new int[n];
Arrays.fill(dp, 1);
for (int i = m - 2; i >= 0; i--) {
for (int j = n - 2; j >= 0; j--) {
dp[j] = dp[j] + dp[j + 1];
}
}
return dp[0];
}
}
leetcode63. 不同路径 II
class Solution {
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
int M = obstacleGrid.length;
int N = obstacleGrid[0].length;
int[][] dp = new int[M][N];
for (int i = M - 1; i >= 0; i--) {
if (obstacleGrid[i][N - 1] == 1) break;
dp[i][N - 1] = 1;
}
for (int i = N - 1; i >= 0; i--) {
if (obstacleGrid[M - 1][i] == 1) break;
dp[M - 1][i] = 1;
}
for (int i = M - 2; i >= 0; i--) {
for (int j = N - 2; j >= 0; j--) {
if (obstacleGrid[i][j] == 1) {
dp[i][j] = 0;
continue;
}
dp[i][j] = dp[i + 1][j] + dp[i][j + 1];
}
}
return dp[0][0];
}
}
leetcode96. 不同的二叉搜索树
class Solution {
public int numTrees(int n) {
int[] dp = new int[n + 1];
dp[0] = 1;
dp[1] = 1;
for (int thisN = 2; thisN <= n; thisN++) {
for (int i = 0; i < thisN; i++) {
dp[thisN] += dp[i] * dp[thisN - i - 1];
}
}
return dp[n];
}
}
leetcode64最小路径和
class Solution {
public int minPathSum(int[][] grid) {
int M = grid.length;
if (M == 0) return 0;
int N = grid[0].length;
if (N == 0) return 0;
for (int i = M - 2; i >= 0; i--) grid[i][N - 1] += grid[i + 1][N - 1];
for (int i = N - 2; i >= 0; i--) grid[M - 1][i] += grid[M - 1][i + 1];
for (int i = M - 2; i >= 0; i--) {
for (int j = N - 2; j >= 0; j--) {
grid[i][j] = Math.min(grid[i + 1][j], grid[i][j + 1]) + grid[i][j];
}
}
return grid[0][0];
}
}
leetcode329. 矩阵中的最长递增路径
class Solution {
int maxLen = 0;
public int longestIncreasingPath(int[][] matrix) {
int m = matrix.length, n = matrix[0].length;
int[][] visited = new int[m][n];//计算以每个节点开头的递增序列的长度
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
maxLen = Math.max(maxLen, dfs(matrix, i, j, m, n, visited, Integer.MIN_VALUE));
}
}
return maxLen;
}
public int dfs(int[][] matrix, int i, int j, int m, int n, int[][] visited, int pre) {
if (i < 0 || i >= m || j < 0 || j >= n || matrix[i][j] <= pre) return 0;
if (visited[i][j] > 0) return visited[i][j];//如果之前已经计算过,直接返回即可
int l = dfs(matrix, i - 1, j, m, n, visited, matrix[i][j]);
int r = dfs(matrix, i + 1, j, m, n, visited, matrix[i][j]);
int up = dfs(matrix, i, j - 1, m, n, visited, matrix[i][j]);
int down = dfs(matrix, i, j + 1, m, n, visited, matrix[i][j]);
visited[i][j] = 1 + Math.max(Math.max(l, r), Math.max(up, down));
return visited[i][j];
}
}
01背包类DP
- 01背包问题本身不难,但是最重要的是如何识别出来题是否为01背包,一般是有一个目标堆,对于数组的留和舍两种选择,通过数组值的取舍进行达到目标堆效果
- 背包问题DP进行空间压缩时,weight循环要从大到小遍历,否则会造成前段值覆盖引起答案错误
leetcode416. 分割等和子集
class Solution {
public boolean canPartition(int[] nums) {
int sum = 0, max = 0;
for (int val : nums) {
sum += val;
max = Math.max(max, val);
}
int target = sum / 2;
if ((sum & 1) == 1 || max > target) return false;
boolean[][] dp = new boolean[nums.length][target + 1];
dp[0][nums[0]] = true;
for (int i = 1; i < nums.length; i++) {
for (int j = 1; j <= target; j++) {
dp[i][j] = dp[i - 1][j];
if (j >= nums[i]) dp[i][j] |= dp[i - 1][j - nums[i]];
}
}
return dp[nums.length - 1][target];
}
}
- 空间压缩
class Solution {
public boolean canPartition(int[] nums) {
int sum = 0, max = 0;
for (int val : nums) {
sum += val;
max = Math.max(max, val);
}
int target = sum / 2;
if ((sum & 1) == 1 || max > target) return false;
boolean[] dp = new boolean[target + 1];
dp[nums[0]] = true;
for (int i = 1; i < nums.length; i++)
for (int j = target; j > 0; j--)
if (j >= nums[i])
dp[j] |= dp[j - nums[i]];// 依赖上一层i-1的行,所以j要从大到小
return dp[target];
}
}
leetcode1049. 最后一块石头的重量 II
class Solution {
public int lastStoneWeightII(int[] stones) {
int sum = 0;
for (int val : stones) sum += val;
int size = sum / 2 + 1;
int[][] dp = new int[stones.length][size];
for (int i = stones[0]; i < size; i++) dp[0][i] = stones[0];
for (int i = 1; i < stones.length; i++) {
for (int j = 1; j < size; j++) {
dp[i][j] = dp[i - 1][j];
if (j >= stones[i])
dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - stones[i]] + stones[i]);
}
}
return sum - dp[stones.length - 1][size - 1] * 2;
}
}
- 空间压缩
class Solution {
public int lastStoneWeightII(int[] stones) {
int sum = 0;
for (int val : stones) sum += val;
int size = sum / 2 + 1;
int[] dp = new int[size];
for (int i = stones[0]; i < size; i++) dp[i] = stones[0];
for (int i = 1; i < stones.length; i++) {
for (int j = size - 1; j >= stones[i]; j--) {
dp[j] = Math.max(dp[j], dp[j - stones[i]] + stones[i]);
}
}
return sum - dp[size - 1] * 2;
}
}
leetcode494. 目标和
class Solution {
public int findTargetSumWays(int[] nums, int s) {
int sum = 0;
for (int num : nums) sum += num;
// 绝对值范围超过了sum的绝对值范围则无法得到
if (Math.abs(s) > Math.abs(sum)) return 0;
int len = nums.length;
int range = sum * 2 + 1;//因为要包含负数所以要两倍,又要加上0这个中间的那个情况
int[][] dp = new int[len][range];//这个数组是从总和为-sum开始的
//加上sum纯粹是因为下标界限问题,赋第二维的值的时候都要加上sum
// 初始化 第一个数只能分别组成+-nums[i]的一种情况
dp[0][sum + nums[0]] += 1;
dp[0][sum - nums[0]] += 1;
for (int i = 1; i < len; i++) {
for (int j = -sum; j <= sum; j++) {
if ((j + nums[i]) > sum) {//+不成立 加上当前数大于了sum 只能减去当前的数
dp[i][j + sum] = dp[i - 1][j - nums[i] + sum];
} else if ((j - nums[i]) < -sum) {//-不成立 减去当前数小于-sum 只能加上当前的数
dp[i][j + sum] = dp[i - 1][j + nums[i] + sum];
} else {//+-都可以
dp[i][j + sum] = dp[i - 1][j + nums[i] + sum] + dp[i - 1][j - nums[i] + sum];
}
}
}
return dp[len - 1][sum + s];
}
}
- 范围优化0 ~(sum-target)/ 2
- 思维转化:将从0到负值m再转化成target,定存在一个正值n使m+n=0,然后转化成target这个过程变成从0直接到target值中将m,n值舍弃的过程。故就转化成了只加或舍弃而不减的01背包问题。
题目详解
class Solution {
public int findTargetSumWays(int[] nums, int target) {
int M = nums.length;
int sum = 0;
for (int i : nums) sum += Math.abs(i);
if (target > sum || (sum - target) % 2 != 0) return 0;
int N = (sum - target) / 2+1;
int[][] dp = new int[M + 1][N] ;
dp[0][0] = 1;
for (int j = 0; j < N; j++) {
if (nums[0] == j) dp[0][j] += 1;
}
for (int i = 1; i < M; i++) {
for (int j = 0; j < N; j++) {
dp[i][j] += dp[i - 1][j];
if (j >= nums[i]) dp[i][j] += dp[i - 1][j - nums[i]];
}
}
return dp[M-1][N-1];
}
}
- 空间压缩
class Solution {
public int findTargetSumWays(int[] nums, int target) {
int M = nums.length;
int sum = 0;
for (int i : nums) sum += Math.abs(i);
if (target > sum || (sum - target) % 2 != 0) return 0;
int N = (sum - target) / 2 + 1;
int[] dp = new int[N];
dp[0] = 1;
for (int j = 0; j < N; j++) {
if (nums[0] == j) dp[j] += 1;
}
for (int i = 1; i < M; i++) {
for (int j = N - 1; j >= 0; j--) {
if (j >= nums[i]) dp[j] += dp[j - nums[i]];
}
}
return dp[N - 1];
}
}
leetcode474. 一和零
- 三维动态规划,压缩后的代码
class Solution {
public int findMaxForm(String[] strs, int m, int n) {
int[][] dp = new int[m + 1][n + 1];
int[] ints = count0and1(strs[0]);
for (String str : strs) {
int[] cur = count0and1(str);
for (int j = m; j >= cur[0]; j--) {// 只有空间压缩的时候才能>=cur[0]
for (int k = n; k >= cur[1]; k--) {// 只有空间压缩的时候才能>=cur[1]
dp[j][k] = Math.max(dp[j][k], dp[j - cur[0]][k - cur[1]] + 1);
}
}
}
return dp[m][n];
}
private int[] count0and1(String str) {
int[] res = new int[2];
for (int i = 0; i < str.length(); i++) {
res[str.charAt(i) - '0']++;
}
return res;
}
}
完全背包
leetcode518. 零钱兑换 II
class Solution {
public int change(int amount, int[] coins) {
int[][] dp = new int[coins.length][amount + 1];
for (int n = 0; n * coins[0] <= amount; n++) {
dp[0][n * coins[0]] = 1;
}
for (int i = 1; i < coins.length; i++) {
for (int j = 0; j <= amount; j++) {
dp[i][j] = dp[i - 1][j];
if (j >= coins[i]) {
dp[i][j] += dp[i][j - coins[i]];
}
}
}
return dp[coins.length - 1][amount];
}
}
- 空间压缩
class Solution {
public int change(int amount, int[] coins) {
int[] dp = new int[amount + 1];
for (int n = 0; n * coins[0] <= amount; n++) {
dp[n * coins[0]] = 1;
}
for (int i = 1; i < coins.length; i++) {
for (int j = coins[i]; j <= amount; j++) {
dp[j] += dp[j - coins[i]];
}
}
return dp[amount];
}
}
leetcode377. 组合总和 Ⅳ
class Solution {
public int combinationSum4(int[] nums, int target) {
int[]dp = new int[target + 1];
dp[0] = 1;
for (int j = 1; j <= target; j++) {//组合加和为j情况下有几种方案
for (int i = 0; i < nums.length; i++) {// 遍历背包,选择可以添加的数
if (j >= nums[i]) {// 如果此时可以添加nums[i]这个数
dp[j] += dp[j - nums[i]];
}
}
}
return dp[target];
}
}
leetcode70爬楼梯(续集)
题目:之前爬楼梯只能一次一个或两个,这次就又给丁一个整数m,可一次一走1 ~ m 次,整数n表示楼梯总数。问共有几种方案。
- 和上一题leetcode377. 组合总和 Ⅳ本质相同
class Solution {
public int combinationSum4(int n, int m) {
int[] dp = new int[n + 1];
dp[0] = 1;
for (int i = 0; i <= n; i++) { // 遍历背包,就是楼层数量
for (int j = 0; j < m; j++) { // 遍历物品,就是遍历步数
if (i - j >= 0) {
dp[i] += dp[i - j];
}
}
}
return dp[n];
}
}
leetcode322. 零钱兑换
- 经典完全背包
class Solution {
public int coinChange(int[] coins, int amount) {
int[][] dp = new int[coins.length][amount + 1];
for (int i = 0; i < coins.length; i++) Arrays.fill(dp[i], 1000000);
for (int i = 0; coins[0] * i <= amount; i++) {
dp[0][coins[0] * i] = i;
}
for (int i = 1; i < coins.length; i++) {
for (int j = 0; j <= amount; j++) {
dp[i][j] = dp[i - 1][j];
for (int n = 0; n * coins[i] <= j; n++) {
dp[i][j] = Math.min(dp[i - 1][j - coins[i] * n] + n, dp[i][j]);
}
}
}
return dp[coins.length - 1][amount] == 1000000 ? -1 : dp[coins.length - 1][amount];
}
}
- 斜率优化
class Solution {
public int coinChange(int[] coins, int amount) {
int[][] dp = new int[coins.length][amount + 1];
for (int i = 0; i < coins.length; i++) Arrays.fill(dp[i], 1000000);
for (int i = 0; coins[0] * i <= amount; i++) {
dp[0][coins[0] * i] = i;
}
for (int i = 1; i < coins.length; i++) {
for (int j = 0; j <= amount; j++) {
dp[i][j] = dp[i - 1][j];
if (j >= coins[i]) {
dp[i][j] = Math.min(dp[i][j], dp[i][j - coins[i]] + 1);
}
}
}
return dp[coins.length - 1][amount] == 1000000 ? -1 : dp[coins.length - 1][amount];
}
}
- 空间压缩
class Solution {
public int coinChange(int[] coins, int amount) {
int[] dp = new int[amount + 1];
Arrays.fill(dp, 1000000);
for (int i = 0; coins[0] * i <= amount; i++) {
dp[coins[0] * i] = i;
}
for (int i = 1; i < coins.length; i++) {
for (int j = coins[i]; j <= amount; j++) {
dp[j] = Math.min(dp[j], dp[j - coins[i]] + 1);
}
}
return dp[amount] == 1000000 ? -1 : dp[amount];
}
}
leetcode279. 完全平方数
class Solution {
public int numSquares(int n) {
int maxN = (int) Math.sqrt(n);
int[] dp = new int[n + 1];
Arrays.fill(dp, 1000000);
dp[0] = 0;// 初始化值。组成0需要0个
for (int i = 1; i <= maxN; i++) {// 背包遍历
for (int j = i * i; j <= n; j++) {// 目标值遍历
dp[j] = Math.min(dp[j - i * i] + 1, dp[j]);
}
}
return dp[n];
}
}
leetcode139. 单词拆分
- 注意stringMaxLen的剪枝
- 回溯超时
class Solution {
List<String> dict;
int stringMaxLen = 0;
public boolean wordBreak(String s, List<String> wordDict) {
if (s.length() < 1) return true;
dict = wordDict;
// 如果某个区间长度大于stringMaxLen,说明比该长度长的区间不可能成功匹配,达到剪枝效果
for (String str : wordDict) {
stringMaxLen = Math.max(stringMaxLen, str.length());
}
boolean[] dp = new boolean[s.length() + 1];
dp[s.length()] = true;
for (int start = s.length() - 1; start >= 0; start--) {
for (int i = start; i < s.length() && i - start + 1 <= stringMaxLen; i++) {
if (dict.contains(s.substring(start, i + 1)) && dp[i + 1]) {
dp[start] = true;
break;
}
}
}
return dp[0];
}
}
- 回溯超时思想
class Solution {
List<String> dict;
int stringMaxLen = 0;
public boolean wordBreak(String s, List<String> wordDict) {
if (s.length() < 1) return true;
dict = wordDict;
for (String str : wordDict) {
stringMaxLen = Math.max(stringMaxLen, str.length());
}
return process(s, 0);
}
private boolean process(String s, int strat) {
if (strat == s.length()) return true;
for (int i = strat; i < s.length() && i - strat + 1 <= stringMaxLen; i++) {
String str = s.substring(strat, i + 1);
if (dict.contains(str)&&process(s, i + 1)) {
return true;
}
}
return false;
}
}
打家劫舍
leetcode198. 打家劫舍
- dp[ i ] 表示前索引 i 个房间能偷的最大值
- 和爬楼梯差不多,不压缩了,懒
class Solution {
public int rob(int[] nums) {
int N = nums.length;
if (N <= 1) return nums[0];
int[] dp = new int[N];
dp[0] = nums[0];
dp[1] = Math.max(nums[0], nums[1]);// 这里不是dp[1] = nums[1];
for (int i = 2; i < N; i++) {
// 两种情况取最优
dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i]);
}
return dp[N - 1];
}
}
leetcode213. 打家劫舍 II
- 两种情况,两个DP
class Solution {
public int rob(int[] nums) {
int N = nums.length;
if (N == 1) return nums[0];
if (N == 2) return Math.max(nums[0], nums[1]);
int[] dp_1 = new int[N - 1], dp_2 = new int[N - 1];
// 允许第一个房间被偷,不允许最后一个被偷的初始化
dp_1[0] = nums[0];
dp_1[1] = Math.max(nums[1], dp_1[0]);
// 不允许第一个房间被偷,允许最后一个被偷的初始化
dp_2[0] = nums[1];
dp_2[1] = Math.max(dp_2[0], nums[2]);
for (int i = 2; i < N - 1; i++) {
// dp_1范围是 nums[0...N-2]
dp_1[i] = Math.max(dp_1[i - 1], dp_1[i - 2] + nums[i]);
// dp_1范围是 nums[1...N-1]
dp_2[i] = Math.max(dp_2[i - 1], dp_2[i - 2] + nums[i + 1]);
}
// 最后取最值
return Math.max(dp_1[N - 2], dp_2[N - 2]);
}
}
leetcode337打家劫舍 III
- 有动态规划的思想,不是严格的动态规划
class Solution {
public int rob(TreeNode root) {
if (root == null) return 0;
transData data = process(root);
return Math.max(data.yes, data.no);
}
private transData process(TreeNode root) {
if (root == null) return new transData(0, 0);
transData l = process(root.left);
transData r = process(root.right);
int yes = root.val + l.no + r.no;
int no = Math.max(l.yes, l.no) + Math.max(r.yes, r.no);
return new transData(yes, no);
}
static class transData {
int yes;
int no;
public transData(int i, int j) {
yes = i;
no = j;
}
}
}
leetcode740. 删除并获得点数
class Solution {
public int deleteAndEarn(int[] nums) {
int[] sum = new int[10001];
for (int val : nums) sum[val] += val;
int pre0 = sum[0], pre1 = Math.max(sum[0], sum[1]), cur = pre1;
for (int i = 2; i < 10001; i++) {
cur = Math.max(pre0 + sum[i], pre1);
pre0 = pre1;
pre1 = cur;
}
return cur;
}
}
股票问题
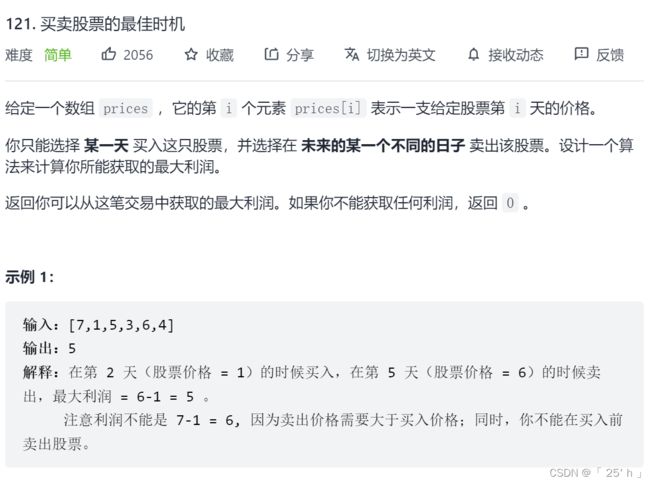
leetcode121. 买卖股票的最佳时机
- 动态规划(不压缩了,没意思)
class Solution {
public int maxProfit(int[] prices) {
int N = prices.length;
if (N <= 1) return 0;
int[][] dp = new int[N][2];
dp[0][0] = prices[0];
dp[0][1] = 0;
for (int i = 1; i < N; i++) {
dp[i][0] = Math.min(dp[i - 1][0], prices[i]);// i或i之前所买入股票的最小值
dp[i][1] = Math.max(dp[i - 1][1], prices[i] - dp[i][0]);// i或i之前卖股票所获的最大利润
}
return dp[N - 1][1];
}
}
- 双指针,时间复杂度和动态规划相同
class Solution {
public int maxProfit(int[] prices) {
int max = 0;
int res = 0;
for (int i = prices.length - 1; i >= 0; i--) {
if (max > prices[i]) res = Math.max(res, max - prices[i]);
max = Math.max(prices[i], max);
}
return res;
}
}
leetcode122. 买卖股票的最佳时机 II
- 递归思想(空间复杂度高,但是能提供思路)
class Solution {
int[] prices;
int N;
public int maxProfit(int[] prices) {
N = prices.length;
this.prices = prices;
return process(0, false);
}
/**
* @param i 当前股票索引
* @param have 当前手里面是否有股票
* @return 利益值
*/
public int process(int i, boolean have) {
if (i == N) return 0;
if (have) return Math.max(process(i + 1, true), process(i + 1, false) + prices[i]);
return Math.max(process(i + 1, false), process(i + 1, true) - prices[i]);
}
}
- 写好暴搜后,动归不用动脑子了
- 打败了低是因为有更优的贪心算法,这里不多说了
class Solution {
public int maxProfit(int[] prices) {
int N = prices.length;
int[][] dp = new int[N + 1][2];
for (int i = N - 1; i >= 0; --i) {
dp[i][1] = Math.max(dp[i + 1][1], dp[i + 1][0] + prices[i]);
dp[i][0] = Math.max(dp[i + 1][0], dp[i + 1][1] - prices[i]);
}
return dp[0][0];
}
}
leetcode714. 买卖股票的最佳时机含手续费
class Solution {
public int maxProfit(int[] prices, int fee) {
int N = prices.length;
int[] dp = new int[2];
for (int i = N - 1; i >= 0; --i) {
int temp=dp[0];
dp[0] = Math.max(dp[0], dp[1] - fee - prices[i]);
dp[1] = Math.max(dp[1], temp + prices[i]);
}
return dp[0];
}
}
leetcode123. 买卖股票的最佳时机 III
- 暴力搜索
class Solution {
int[] prices;
int N;
public int maxProfit(int[] prices) {
this.prices=prices;
N = prices.length;
if (N <= 1) return 0;
return process(0, false, 0);
}
private int process(int i, boolean have, int num) {
if (num == 2 || i == N) return 0;
if (have) return Math.max(process(i + 1, true, num),
process(i + 1, false, num + 1) + prices[i]);
return Math.max(process(i + 1, false, num),
process(i + 1, true, num) - prices[i]);
}
}
- 递归转动规
class Solution {
public int maxProfit(int[] prices) {
int N = prices.length;
if (N <= 1) return 0;
int[][][] dp = new int[N + 1][2][2];
for (int i = N - 1; i >= 0; --i) {
dp[i][1][1] = Math.max(dp[i + 1][1][1], prices[i]);
dp[i][1][0] = Math.max(dp[i + 1][1][0], dp[i + 1][0][1] + prices[i]);
dp[i][0][1] = Math.max(dp[i + 1][0][1], dp[i + 1][1][1] - prices[i]);
dp[i][0][0] = Math.max(dp[i + 1][0][0], dp[i + 1][1][0] - prices[i]);
}
return dp[0][0][0];
}
}
- 空间压缩
class Solution {
public int maxProfit(int[] prices) {
int N = prices.length;
if (N <= 1) return 0;
int[][] dp = new int[2][2];
for (int i = N - 1; i >= 0; --i) {
//依赖关系 11 --> 01 --> 10 --> 00
//填充关系 00 --> 10 --> 01 --> 11 严格不能变
dp[0][0] = Math.max(dp[0][0], dp[1][0] - prices[i]);
dp[1][0] = Math.max(dp[1][0], dp[0][1] + prices[i]);
dp[0][1] = Math.max(dp[0][1], dp[1][1] - prices[i]);
dp[1][1] = Math.max(dp[1][1], prices[i]);
}
return dp[0][0];
}
}
leetcode188. 买卖股票的最佳时机 IV
- 暴力递归 —> 动态规划 —> 空间压缩
class Solution {
public int maxProfit(int k, int[] prices) {
int N = prices.length;
if (N <= 1) return 0;
int[][] dp = new int[2][k + 1];
for (int i = N - 1; i >= 0; --i) {
for (int j = 0; j < k; j++) {
// 严格依赖填表顺序
dp[0][j] = Math.max(dp[0][j], dp[1][j] - prices[i]);
dp[1][j] = Math.max(dp[1][j], dp[0][j + 1] + prices[i]);
}
}
return dp[0][0];
}
}
leetcode309. 最佳买卖股票时机含冷冻期
- 暴搜超时
class Solution {
int N;
int[] prices;
public int maxProfit( int[] prices) {
this.N = prices.length;
if (N <= 1) return 0;
this.prices=prices;
return process(0,false,false);
}
private int process(int i, boolean have, boolean FreePeriod) {
if (i == N) return 0;
if (have) return Math.max(process(i + 1, true, false),
process(i + 1, false, true) + prices[i]);
if (FreePeriod) return process(i + 1, false, false);
return Math.max(process(i + 1, false, false),
process(i + 1, true, false) - prices[i]);
}
}
- 经典三维动态规划
class Solution {
public int maxProfit(int[] prices) {
int N = prices.length;
if (N <= 1) return 0;
int[][][] dp = new int[N + 1][2][2];
for (int i = N - 1; i >= 0; --i) {
dp[i][0][0] = Math.max(dp[i + 1][0][0], dp[i + 1][1][0] - prices[i]);
dp[i][0][1] = dp[i + 1][0][0];
dp[i][1][0] = Math.max(dp[i + 1][1][0], dp[i + 1][0][1] + prices[i]);
}
return dp[0][0][0];
}
}
- 压缩的动态规划
class Solution {
public int maxProfit(int[] prices) {
int N = prices.length;
if (N <= 1) return 0;
int[][] dp = new int[2][2];
for (int i = N - 1; i >= 0; --i) {
int temp=dp[0][0];
dp[0][0] = Math.max(dp[0][0], dp[1][0] - prices[i]);
dp[1][0] = Math.max(dp[1][0], dp[0][1] + prices[i]);
dp[0][1] = temp;
}
return dp[0][0];
}
}
序列问题
leetcode300. 最长递增子序列
class Solution {
public int lengthOfLIS(int[] nums) {
int N = nums.length, res = 0;
int[] dp = new int[N];// dp[i]是指以nums[i]为序列结尾的最长子序列长度
for (int i = 0; i < N; i++) {
int curMax = 0;
for (int j = i - 1; j >= 0; --j) {
if (nums[i] > nums[j]) {// 比nums[i]小的才能成为nums[i]左边的序列
curMax = Math.max(curMax, dp[j]);
}
}
dp[i] = curMax + 1;// 前面最长的加上nums[i]
res = Math.max(res, dp[i]);// 记录最长结果
}
return res;
}
}
- dp[ i ]的下标作为结果值,dp值作为满足 i + 1 长度的子序列最小值。用二分查找
class Solution {
public int lengthOfLIS(int[] nums) {
int N = nums.length, res = -1;
if (N <= 1) return N;
int[] dp = new int[N];
for (int val : nums) {
if (res == -1 || dp[res] < val) dp[++res] = val;
else dp[minNumOfBigger(dp, res, val)] = val;
}
return res + 1;
}
private int minNumOfBigger(int[] dp, int right, int target) {
int left = 0;
while (left < right) {
int mid = (left + right) / 2;
if (dp[mid] == target) return mid;
else if (dp[mid] > target) right = mid;
else left = mid + 1;
}
return left;
}
}
leetcode354. 俄罗斯套娃信封问题
class Solution {
// 先对宽度w进行升序排序,如果遇到w相同的情况,则按照高度h降序排序。
// 之后把所有的h作为一个数组,在这个数组上计算 LIS(最长递增子序列) 的长度就是答案。
// 这个问题转化思路真的太绝了,这样就保证了 w 值定满足答案情况下,h 最长递增就是结果,从而二维转为一维运算
public int maxEnvelopes(int[][] envelopes) {
int N = envelopes.length;
if (N <= 1) return 1;
// w值升序排列,h值降序排列
Arrays.sort(envelopes, (o1, o2) -> o1[0] != o2[0] ? Integer.compare(o1[0], o2[0]) : Integer.compare(o2[1], o1[1]));
int[] dp = new int[N];
int k = -1;// 初始值
for (int[] envelope : envelopes) {
if (k == -1 || envelope[1] > dp[k]) dp[++k] = envelope[1];
else dp[binarySearchMinOfBiggerNum(dp, 0, k, envelope[1])] = envelope[1];
}
return k + 1;
}
// 和最长递增子序列题目的 dp 思路相同
private int binarySearchMinOfBiggerNum(int[] dp, int left, int right, int target) {
while (left < right) {
int mid = (left + right) / 2;
if (dp[mid] >= target) right = mid;
else left = mid + 1;
}
return right;
}
}
leetcode1143. 最长公共子序列
class Solution {
public int longestCommonSubsequence(String text1, String text2) {
int M = text1.length(), N = text2.length();
int[][] dp = new int[M][N];
dp[0][0] = text1.charAt(0) == text2.charAt(0) ? 1 : 0;
for (int i = 1; i < M; ++i) {
dp[i][0] = Math.max(dp[i - 1][0], text1.charAt(i) == text2.charAt(0) ? 1 : 0);
}
for (int i = 1; i < N; ++i) {
dp[0][i] = Math.max(dp[0][i - 1], text1.charAt(0) == text2.charAt(i) ? 1 : 0);
}
for (int i = 1; i < M; ++i) {
for (int j = 1; j < N; ++j) {
dp[i][j] = Math.max(dp[i][j - 1], dp[i - 1][j]);
if (text1.charAt(i) == text2.charAt(j)) {
dp[i][j] = Math.max(dp[i - 1][j - 1] + 1, dp[i][j]);
}
}
}
return dp[M - 1][N - 1];
}
}
- 空间压缩
class Solution {
public int longestCommonSubsequence(String text1, String text2) {
int M = text1.length(), N = text2.length();
int[] dp = new int[N];
dp[0] = text1.charAt(0) == text2.charAt(0) ? 1 : 0;
for (int i = 1; i < N; ++i) {
dp[i] = Math.max(dp[i - 1], text1.charAt(0) == text2.charAt(i) ? 1 : 0);
}
for (int i = 1; i < M; ++i) {
// 注意dp[0]的初始化
dp[0] = Math.max(dp[0], text1.charAt(i) == text2.charAt(0) ? 1 : 0);
int pre = dp[0];// 记录上一层循环值为下一层循环做dp[i-1][j-1]的值
for (int j = 1; j < N; ++j) {
int temp = dp[j];
dp[j] = Math.max(dp[j - 1], dp[j]);
if (text1.charAt(i) == text2.charAt(j)) {
dp[j] = Math.max(pre + 1, dp[j]);
}
pre = temp;
}
}
return dp[N - 1];
}
}
leetcode583. 两个字符串的删除操作
- 和最长公共子序列一毛一样
class Solution {
public int minDistance(String word1, String word2) {
int M = word1.length(), N = word2.length();
int[][] dp = new int[M][N];
dp[0][0] = word1.charAt(0) == word2.charAt(0) ? 1 : 0;
for (int i = 1; i < M; ++i) {
dp[i][0] = Math.max(dp[i - 1][0], word1.charAt(i) == word2.charAt(0) ? 1 : 0);
}
for (int i = 1; i < N; ++i) {
dp[0][i] = Math.max(dp[0][i - 1], word1.charAt(0) == word2.charAt(i) ? 1 : 0);
}
for (int i = 1; i < M; ++i) {
for (int j = 1; j < N; ++j) {
dp[i][j] = Math.max(dp[i][j - 1], dp[i - 1][j]);
if (word1.charAt(i) == word2.charAt(j)) {
dp[i][j] = Math.max(dp[i - 1][j - 1] + 1, dp[i][j]);
}
}
}
return M + N - 2 * dp[M - 1][N - 1];
}
}
leetcode1035. 不相交的线
- 本质还是最长不重复子序列
class Solution {
public int maxUncrossedLines(int[] nums1, int[] nums2) {
int M = nums1.length,N=nums2.length;
int[][] dp = new int[M][N];
dp[0][0] = nums1[0] == nums2[0] ? 1 : 0;
for (int i = 1; i < M; i++) {
dp[i][0] = Math.max(dp[i - 1][0], nums1[i] == nums2[0] ? 1 : 0);
}
for (int i=1;i<N;i++){
dp[0][i] = Math.max(dp[0][i - 1], nums1[0] == nums2[i] ? 1 : 0);
}
for (int i = 1; i < M; i++) {
for (int j = 1; j < N; j++) {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
if (nums1[i] == nums2[j]) dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - 1] + 1);
}
}
return dp[M - 1][N - 1];
}
}
leetcode718. 最长重复子数组
class Solution {
public int findLength(int[] nums1, int[] nums2) {
int M = nums1.length, N = nums2.length;
int[][] dp = new int[M][N];
int res = 0;// 记录最大值
for (int i = 0; i < M; i++) {// 初始化
if (nums1[i] == nums2[0]) {
dp[i][0] = 1;
res = 1;
}
}
for (int i = 0; i < N; i++) {// 初始化
if (nums1[0] == nums2[i]) {
dp[0][i] = 1;
res = 1;
}
}
// dp依赖关系
for (int i = 1; i < M; i++) {
for (int j = 1; j < N; j++) {
if (nums1[i] == nums2[j]) {
dp[i][j] = dp[i - 1][j - 1] + 1;
res = Math.max(res, dp[i][j]);
}
}
}
return res;
}
}
leetcode115. 不同的子序列
- 暴搜
class Solution {
int M, N;
String s, t;
public int numDistinct(String s, String t) {
M = s.length();
N = t.length();
this.s = s;
this.t = t;
return process(0, 0);
}
private int process(int allIndex, int tarIndex) {
if (tarIndex == N) return 1;
if (allIndex == M) return 0;
if (s.charAt(allIndex) != t.charAt(tarIndex)) return process(allIndex + 1, tarIndex);
return process(allIndex + 1, tarIndex) + process(allIndex + 1, tarIndex + 1);
}
}
class Solution {
public int numDistinct(String s, String t) {
int M = s.length(), N = t.length();
int[][] dp = new int[M + 1][N + 1];
for (int i = 0; i <= M; i++) dp[i][N] = 1;
for (int i = M - 1; i >= 0; i--) {
for (int j = N - 1; j >= 0; j--) {
dp[i][j] = dp[i + 1][j];
if (s.charAt(i) == t.charAt(j)) dp[i][j] += dp[i + 1][j + 1];
}
}
return dp[0][0];
}
}
leetcode72. 编辑距离
class Solution {
public int minDistance(String word1, String word2) {
if (word1 == null || word2 == null) {
return 0;
}
char[] chs1 = word1.toCharArray();
char[] chs2 = word2.toCharArray();
int row = chs1.length + 1;
int col = chs2.length + 1;
int[][] dp = new int[row][col];
//0个字符变成i个的添加距离
for (int i = 1; i < row; i++) {
dp[i][0] = i;
}
//j个字符变成0个的删除距离
for (int j = 1; j < col; j++) {
dp[0][j] = j;
}
for (int i = 1; i < row; i++) {
for (int j = 1; j < col; j++) {
//替换代价
if (chs1[i - 1] == chs2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1];
} else {
dp[i][j] = dp[i - 1][j - 1] +1;
}
/*
dp[i][j - 1] + 1:
i个转化成j-1长度的代价+一个添加距离
dp[i - 1][j] + 1:
i-1个转化成j长度的代价+一个删除距离
*/
dp[i][j] = Math.min(dp[i][j], dp[i][j - 1] + 1);
dp[i][j] = Math.min(dp[i][j], dp[i - 1][j] + 1);
}
}
return dp[row - 1][col - 1];
}
}
leetcode647. 回文子串
- 一般回文的动态规划都是初始化主对角线
class Solution {
public int countSubstrings(String s) {
int N = s.length();
boolean[][] dp = new boolean[N][N];
for (int i = 0; i < N; i++) dp[i][i] = true;
int res = N;
for (int i = N - 2; i >= 0; i--) {
for (int j = i + 1; j < N; j++) {
if (s.charAt(i) == s.charAt(j) && (j - i == 1 || dp[i + 1][j - 1])) {
res++;
dp[i][j] = true;
}
}
}
return res;
}
}
leetcode516. 最长回文子序列
class Solution {
public int longestPalindromeSubseq(String s) {
int N = s.length();
int[][] dp = new int[N][N];
for (int i = 0; i < N; i++) dp[i][i] = 1;
int res = 1;
for (int i = N - 2; i >= 0; i--) {
for (int j = i + 1; j < N; j++) {
dp[i][j] = Math.max(dp[i + 1][j], dp[i][j - 1]);
if (s.charAt(i) == s.charAt(j)) {// 不用管j-i长度,因为j-i<=1时dp[i + 1][j - 1]为零
dp[i][j] = Math.max(dp[i][j], dp[i + 1][j - 1] + 2);
}
res = Math.max(res, dp[i][j]);
}
}
return res;
}
}
leetcode5. 最长回文子串
class Solution {
public String longestPalindrome(String s) {
if (s == null || s.length() == 0) return "";
int N = s.length();
boolean[][] dp = new boolean[N][N];
for (int i = 0; i < N; i++) dp[i][i] = true;
int maxPre = 0, maxLen = 1;
for (int i = N - 1; i >= 0; i--) {
for (int j = i + 1; j < N; j++) {
if (s.charAt(i) == s.charAt(j) && (j - i <= 1 || dp[i + 1][j - 1])) {
if (j - i + 1 > maxLen) {
maxLen = j - i + 1;
maxPre = i;
}
dp[i][j] = true;
}
}
}
return s.substring(maxPre, maxPre + maxLen);
}
}