lower_bound和upper_bound的用法

一、一般数组

先看一段简单代码

#include
using namespace std;
int cmd(int a,int b)
{
	return a>b;
}
int main()
{
	int a[8]={7,5,3,1,6,9,6,2};
	sort(a,a+8);
	for(int i=0;i<8;i++)
	{
		cout<())-a;
	int pos4=upper_bound(a,a+8,4,greater())-a;
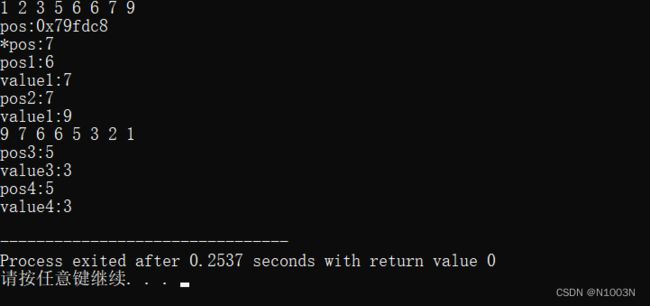
	cout<<"pos3:"<

输出结果： 

可以注意一下，这里输出的时候写pos代表地址，*pos代表数值。

int *pos=lower_bound(a,a+8,7);

cout<<"pos:"<<pos<

cout<<"*pos:"<<*pos<

可知lower_bound(a,a+8,7)-a找到的是第一个不小于也就是大于等于7的数的下标，从而可得到第一个大于等于7的数值为a[6]即7。

同理upper_bound(a,a+8,7)-a找到的是第一个大于查找数的下标，从而可得第一个大于7的数值为a[7]即9。

接下来看lower_bound(a,a+8,4,greater())-a找到的是起始位置到（末尾位置-1）中第一个小于等于查找数的数的下标。

接下来看upper_bound(a,a+8,4,greater())-a找到的是起始位置到（末尾位置-1）中第一个小于查找数的数的下标。

总结一下：

lower_bound(数组名，数组名+数组长度，要查找的数字)-数组名

可以找到第一个不小于即大于等于要查找数字的数的下标

upper_bound(数组名，数组名+数组长度，要查找的数字)-数组名

可以找到第一个大于要查找数字的数的下标

lower_bound(数组名，数组名+数组长度，要查找的数字,greater())-数组名

可以找到第一个小于等于要查找数字的数的下标

upper_bound(数组名，数组名+数组长度，要查找的数字,greater())-数组名

可以找到第一个小于要查找数字的数的下标

二、vector数组

依然先看代码

#include
using namespace std;
int main()
{
	vectorans;
	ans.push_back(7);
	ans.push_back(3);
	ans.push_back(5);
	ans.push_back(4);
	ans.push_back(6);
	sort(ans.begin(),ans.end());
	//3 4 5 6 7
	for(int i=0;i

输出结果

 和一般数组几乎没什么区别，形式为lower_bound(ans.begin(),ans.end(),4)-ans.begin()，找到的是下标，要表示相应的数值可以写ans[pos1]，也可以写成下面这样：

int p1=*lower_bound(ans.begin(),ans.end(),4);

这里的p1就是相应的数值。

upper_bound用法同理。

总结一下：

lower_bound(数组名.begin()，数组名.end()，要查找的数字)-数组名.begin()

upper_bound(数组名.begin()，数组名.end()，要查找的数字)-数组名.begin()

常用：

以这段代码为例

#include
using namespace std;
int main()
{
	int a[8]={1,3,4,4,4,20,21,22};
	int pos1=lower_bound(a,a+8,4)-a;
	cout<<"pos1:"<

有四个问题：

1.找数值为4的最小下标

2.找第一个数值大于等于4的下标

3.找第一个数值大于4的下标

4.数组中4的个数

对应上面四个问题：

第一二问用lower_bound(a,a+8,4)-a;

第三问用upper_bound(a,a+8,4)-a;

第四问用upper_bound(a,a+8,4)-lower_bound(a,a+8,4)-a;