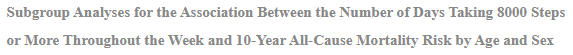JAMA子刊 | So easy! 多走路就可以降低死亡的风险（一区 IF=13.8）

郑老师统计课程，欢迎点击报名：Nhanes公共数据库挖掘 课程

现在微信运动还是比较流行，没事总爱看看自已，看看朋友们每天走了多少步数，JAMA子肝发表一周3次，每天步数在8000以上，可以降低死亡风险的。

So easy! 谁的微信步数还不是1万多步！！

2023年3月，日本京都大学学者在《JAMA Netw Open》（一区，IF=13.8）发表题为：" Association of Daily Step Patterns With Mortality in US Adults" 的研究论文。

这项研究是基于来自2005-2006 年国家健康和营养检查调查（NHANES）中 20 岁或以上的参与者。目的是评估在美国成年人中，一个人走8000步或更多步的天数与死亡率之间的剂量-反应关系。参与者按每周走8000步或以上的天数（0天，1-2天和3-7天）进行分组。使用多变量普通最小二乘回归模型估计10年随访期间全因和心血管死亡率的调整风险差（aRDs），调整潜在的混杂因素。结果表明，每周走 8000 步或更多步的天数与全因死亡率和心血管死亡率的降低呈曲线关系，保护性关联在每周3天达到稳定，这些研究结果表明，人们可以通过每周步行几天获得实质性的健康益处。

摘要与主要结果

一、摘要

背景：以前的研究表明，经常步行的人，特别是每天走8000步或更多步的人，死亡率较低。然而，人们对每周只进行几天高强度步行的健康益处知之甚少。目的是评估在美国成年人中，一个人走8000步或更多的天数与死亡率之间的剂量-反应关系。

方法：这项队列研究评估了 2005-2006 年国家健康和营养检查调查中 20 岁或以上的参与者的代表性样本，他们佩戴加速度计 1 周，并评估了截至 2019年12月31日的死亡率数据。数据分析时间为 2022年4月1日至2023年1月31日。参与者按每周走8000步或以上的天数（0天，1-2天和3-7天）进行分组。使用多变量普通最小二乘回归模型估计10年随访期间全因和心血管死亡率的调整风险差（aRDs），调整潜在的混杂因素（例如，年龄，性别，种族和民族，保险状况，婚姻状况，吸烟，合并症和平均每日步数）。

结果：在3101名参与者（平均[SD]年龄，50.5[18.4]岁;1583名[51.0%]女性和1518名[49.0%]男性;666名[21.5%]黑人，734名[23.7%]西班牙裔，1579名[50.9%]白人和122名[3.9%]其他种族和民族），632名（20.4%）一周中的任何一天都没有走8000步或以上，532名（17.2%）每周1至2天走8000步或以上， 1937年（62.5%）每周3至7天走8000步或更多步。在10年的随访中，全因和心血管死亡分别发生在439名（14.2%）和148名（5.3%）受试者中。与每周0天步行8000步或以上的受试者相比，每周1至2天步行8000步或以上（aRD，-14.9%;95%CI，-18.8%至-10.9%）和每周3至7天（aRD，-16.5%;95%CI，-20.4%至-12.5%）的受试者的全因死亡风险较低。全因和心血管死亡风险的剂量反应相关性呈曲线;保护性关联在每周3天达到稳定。每日步数在6000到10000之间的不同阈值产生了相似的结果。

结论：在这项针对美国成年人的队列研究中，每周走 8000 步或更多步的天数与全因死亡率和心血管死亡率的降低呈曲线关系。这些研究结果表明，人们可以通过每周步行几天获得实质性的健康益处。

二、研究结果

1.分析样本包括3101名参与者(平均[SD]年龄50.5[18.3]岁;女性1583人(51.0%)，男性1518人(49.0%);666名[21.5%]黑人，734名[23.7%]西班牙裔，1579名[50.9%]白人，122名[3.9%]其他种族和民族)。平均每日步数的中位数(IQR)为8793(6238- 11439)步。在参与者中，632人(20.4%)每周0天走8000步或更多，532人(17.2%)每周1至2天走8000步或更多，1937人(62.5%)每周3至7天走8000步或更多。与每周走8000步或更多天的参与者相比，每周走8000步或更多天的参与者更有可能是年轻人、男性、西班牙裔、有保险、已婚、从不吸烟，更不容易肥胖、使用他汀类药物、有合并症(即eGFR降低、糖尿病、高血压、心血管疾病、癌症、肺气肿)、活动受限，或将自己的健康评价为一般或较差(表1)。

缩写：BMI，体重指数(以公斤为单位的体重除以以米为单位的身高的平方);eGFR，估计肾小球滤过率。

a其他种族和民族包括美洲印第安人或阿拉斯加原住民，亚洲人，夏威夷原住民或太平洋岛民，多种族或民族，或未知。

b行动能力限制定义为自我报告在没有特殊设备的情况下行走0.25英里或爬10级楼梯的困难。没有报告这些困难的参与者被认为没有活动限制。

2.采取推荐步骤的天数与全因死亡率和心血管死亡率

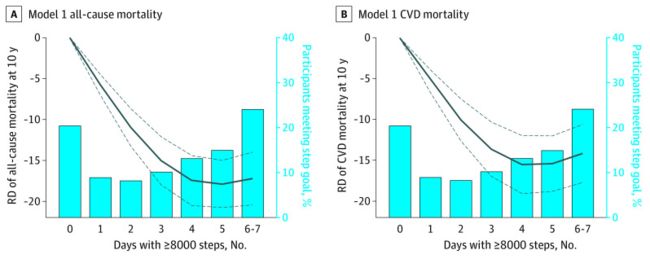
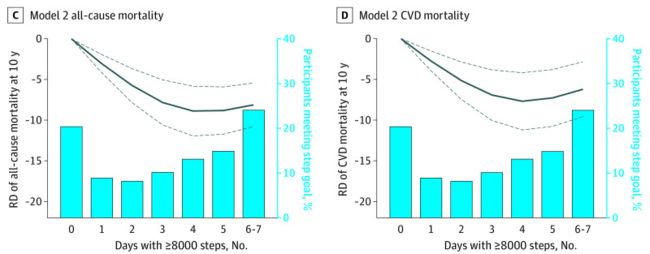
在10年的随访中，确定了439例(14.2%)死于各种原因，148例(5.3%)死于心血管疾病。在调整了潜在的混杂因素后，与每周0天走8000步或更多的参与者相比，每周1至2天走8000步或更多的参与者的10年全因死亡风险降低了14.9% (aRD，- 14.9%;95% CI，−18.8%至−10.9%)，而每周3至7天走8000步或更多步的人则降低16.5% (aRD，−16.5%;95% CI，−20.4%至−12.5%)(表2);同样，与每周0天相比，每周1-2天步行8000步或以上的人10年心血管死亡风险降低8.1% (aRD，−8.1%;95% CI，-11.8%至-4.4%)，而每周3至7天走8000步或更多步的人则降低8.4% (aRD，- 8.4%;95% CI，-12.5%至-4.4%)。限制性立方样条模型显示，每周走8000步或更多的天数与全因死亡率和心血管死亡率之间存在曲线关系;10年的死亡风险随着每周走8000步或更多的天数的增加而迅速下降，并在3至4天达到稳定(图1)。即使在调整了平均每日步数后，这种模式仍然存在。

a模型1包括年龄;性;种族和民族;保险状态;婚姻状况;吸烟;身体质量指数;估计肾小球滤过率;他汀类药物使用;以及糖尿病、高血压、心血管疾病、癌症和肺气肿的病史。除了模型1中的协变量外，模型2还包括平均每日步数。敏感度分析的结果，另外调整收入，流动性限制，和自评健康状况如表3所示，在补充1。

实线表示点估计;虚线表示95% CI。模型1包括年龄;性;种族和民族;保险状态;婚姻状况;吸烟;身体质量指数;估计肾小球滤过率;他汀类药物使用;糖尿病、高血压、心血管疾病、癌症和肺气肿病史。除了模型1中的协变量外，模型2还包括平均每日步数。RD表示风险差异。

3.年龄和性别的分层分析

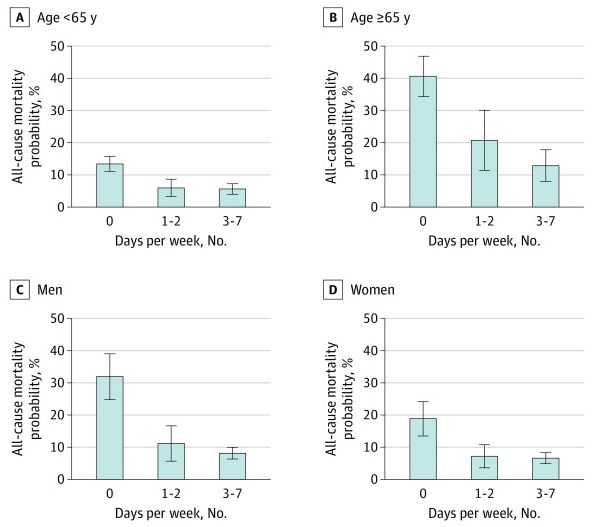
在分层分析中，当年轻和老年参与者每周走8000步或超过1-2天时，他们10年的全因死亡风险都较低(年龄<65岁:aRD，-7.4% [95% CI,-11.2%至-3.7%];≥65岁:aRD，−19.9% [95% CI,−30.8%至-8.9%];p交互=0.04)或每周3至7天(<65岁:aRD，−7.8% [95% CI，−10.3%至−5.2%];≥65岁:aRD，−27.7% [95% CI,−−36.5% 19.0%];p交互<0.001)vs每周0天(图2;我们还发现，当参与者每天1到2天走8000步或更多步时，无论性别，10年全因死亡风险都较低(男性:aRD，-20.8% [95% CI，-28.6%至-13.0%];女性:aRD，-11.6% [95% CI，-16.5%至-6.7%];p交互=0.07，或每周3至7天(男性:aRD，−23.8% [95% CI，−30.4%至−17.2%];女性:aRD，−12.2%[−18.3%至−6.1%];p交互=0.03)vs每周0天(图2;表2见补编1)。

基于回归模型，估计了每种暴露状态下全因死亡率的调整概率，确定了每个类别级别的个体特征，并对全国样本进行平均。模型根据年龄进行了调整;性;种族和民族;保险状态;婚姻状况;吸烟;身体质量指数;估计肾小球滤过率;他汀类药物使用;糖尿病、高血压、心血管疾病、癌症、肺气肿病史;平均每日步数。

4.基于每日步数不同阈值的敏感性分析

当我们使用不同的推荐每日步数阈值时，我们发现了类似的模式(见附录1中的图2)。例如，调整后的10年全因死亡风险在每周1至2天走10000步或更多的参与者中为8.1%，而在每周3至7天和每周0天走10000步或更多的参与者中分别为7.3%和16.7%。同样，在每周1-2天走1万步或以上的参与者中，调整后的10年心血管死亡风险分别为2.4%，而在每周3-7天和每周0天走1万步或以上的参与者中，调整后的10年心血管死亡风险分别为2.3%和7.0%。

5.其他敏感性分析

全因死亡率相对风险量表上的E值，与每周0天相比，每周1至2天为2.50，每周3至7天为2.66，显示的效果能够解释观察到的无边无际的每日步骤模式和死亡率之间的联系需要相当大(即风险率> 2.50的条件协变量测量包括在回归模型不存在日常步数和死亡率之间的联系)。同样，心血管死亡率相对风险量表上的E值，与每周0天相比，每周1-2天为2.34，每周3-7天为2.40。协变量的逆概率加权方法,包括所有在模型1中,我们估计RDs接近零的全因死亡率(与每周0天相比，每周1-2天(aRD，−7.2% [95%CI,-11.4%至-3.0%])和每周3-7天(aRD，−10.6% [95%CI,−14.5%至-6.6%])和心血管死亡率(与每周0天相比，每周1-2天(aRD，−2.0% [95%CI,−4.6%至0.6%])和每周3-7天(aRD，−4.0% [95%CI,−6.2%至1.7%])。当我们对贫困收入比、流动性限制和自评健康进行额外调整时，估计的RDs也更接近于零(补充1中的表3)。当我们将分析限制在使用有效加速度计测量至少6天的个人(补充1中的表4)和那些平均每日步数至少为2000或更多的人(补充1中的表5)时，结果没有发生定性变化。每周1-2天和每周3-7天的全因死亡率校正相对危险度分别为0.75 (95% CI, 0.59-0.96)和0.64 (95% CI, 0.42-0.99)，而每周0天的全因死亡率校正相对危险度为0(附录1中的表6)。

设计与统计学方法

一、研究设计

P（Population）参与者：基于来自2005-2006 年国家健康和营养检查调查（NHANES）中 20 岁或以上的参与者，并与 2019 年之前的全国死亡指数相关联。

E（exposure）暴露因素：参与者按每周走8000步或以上的天数（0天，1-2天和3-7天）进行分组。

O（outcome）结局：主要结局是随访10年时获得全因死亡率。次要结局是随访10年的心血管死亡率。

S（Study design）研究类型：队列研究。

二、统计方法

1.分析在2022年4月1日至2023年1月31日之间进行。我们使用具有Huber-White稳健性SEs的多变量普通最小二乘(OLS)模型来估计10年后每个活动组的全因死亡率和心血管死亡率的调整风险差异(aRDs)和95%CI，这些活动组由他们在一周内走8000步或以上的天数定义(1-2天和3-7天;参照组，0天)。模型1包括年龄调整;性;自我报告的种族和民族;保险状态;婚姻状况;吸烟;体重指数;估计肾小球滤过率(eGFR);他汀类药物使用;以及糖尿病、高血压、心血管疾病、癌症和肺气肿的病史。在模型2(我们的主要模型)中，我们进一步调整了平均每日步数。该模型不包括步数强度，因为之前使用该队列的一项研究表明步数强度与死亡率之间存在零关联。 

2.为了进一步评估参与者每周走8000步或以上的天数与死亡率之间可能的剂量-反应关联，我们在第10、50和90个百分位数使用了3节的限制性立方样条函数。此外，为了评估年龄和性别之间的关联模式，我们在最终的OLS回归模型中纳入了暴露与年龄(<65岁vs≥65岁)或性别(男性vs女性)之间的附加相互作用项。在这些分析中，我们使用Stata中的margin命令，基于OLS回归模型计算了各组全因死亡率的调整概率;也就是说，我们通过在每个类别的每个级别上固定个体特征来估计每个子组的概率，并在我们的国家样本上取平均值(称为预测边际的边际标准化形式)。

3.我们还进行了几次敏感性分析（附录1中的eMethods 3）。在所有分析中，NHANES调查权重用于解释选择参与者的不平等概率以及合格和接近的个人的无响应。使用R版本4.0.2（R统计计算基金会）和Stata版本17（StataCorp LLC）软件进行统计分析。统计代码示例在补编 1 的电子方法 4 中描述。所有假设检验均为2侧，P <0.05被认为具有统计学意义。

小  结

限制性立方样图，非线性关系现在文章当中用的越来越多，如果你研究的主要因素也是定量数据的，不妨用这方法试试，有可能可以发现意外的结果。

一个专门做公共数据库的公众号，关注我们