数据结构——线性表

本文内容是自己通过对本章的学习，概括汇总知识点以及加上自己的理解而写。不会有很多的概念性定义。而是旨在对大家该章知识框架的形成提供帮助，包括对知识的复盘，并且用最通俗的语言来帮助大家理解我所认为重要的知识。

如果你是来进行系统的学习，那么本文可能只是用来拓展知识面；但如果你是在学习相关内容后，对于框架体系的建立比较模糊，以及部分知识点存在疑惑，那么本文应该非常适合你。
 

先简单介绍本章的内容：

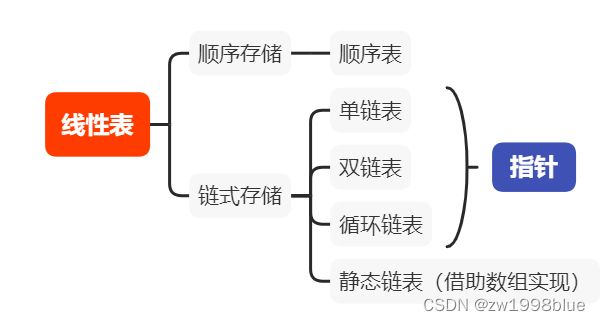
 线性表中的内容主要有两部分：一个是线性表的定义和基本操作，一个是线性表的实现。无外乎就是线性表这个数据结构的三要素：线性表的定义就是逻辑结构，实现方式就是存储结构，基本操作就是运算。首先以线性表的存储结构分类，在顺序存储和链式存储中分别详细介绍基本操作的原理和C++代码实现，最后再扩展一些线性表的应用。进行一个本章的总结。

目录

定义和基本操作

顺序表

基本操作实现

链表

单链表基本操作

双链表

循环链表

静态链表

---

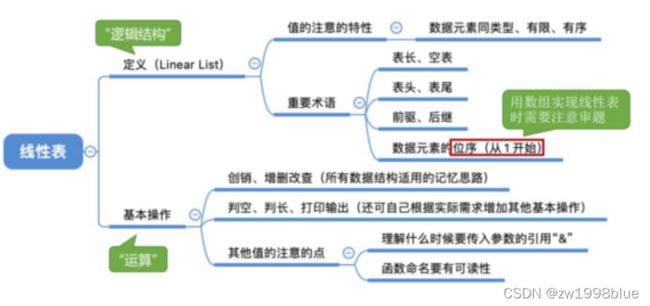
定义和基本操作

线性表的定义：线性表是由n个相同类型的元素组成的有序序列，一般用L表示。

基本操作：初始化、求表长、按值查找、按位查找、插入、删除、输出、判空、销毁、

---

顺序表

首先来看一下线性表用顺序存储——顺序表来如何实现。

顺序表可以分为静态分配和动态分配。静态分配中，数组大小已固定，可能会产生溢出导致程序崩溃；动态分配不必提前分配数组大小，一但原空间占满，就会另外开辟更大的存储空间替换原空间，达到扩充存储空间的目的。

注意：动态分配属于顺序存储，不是链式存储。本质上物理结构没有变，仍是随机存取

typedef int Elemtype;
typedef struct { 
	Elemtype elem[MaxSize];
	int length;
}SqList;
typedef struct {
	Elemtype *elem;
	int length;
}SeqList;

增加一个新结点就需要在内存中申请该结点所需空间

c:L.data=(ElemType*)malloc(sizeof(ElemType)*InitSize);

c++:L.data=new ElemType[InitSize];

new和delete, malloc和free 比较

属性上，new/delete是C++关键字，需要编译器支持。malloc/free是库函数，需要头文件支持。

在使用上，他们都可用于申请动态内存和释放内存。new/delete比malloc/free更加智能，其实底层也是执行的malloc/free。为啥说new/delete更加的智能？因为new和delete在对象创建的时候自动执行构造函数，对象消亡之前会自动执行析构函数。

在返回类型上，new操作符内存分配成功时，返回的是对象类型的指针，类型严格与对象匹配，无须进行类型转换，故new是符合类型安全性的操作符。而malloc内存分配成功则是返回void * ，需要通过强制类型转换将void*指针转换成我们需要的类型。

int *p;    p = new int; //返回类型为int*类型，大小为sizeof(int);

int *pa; pa = new int[50];//返回类型为int *，大小为sizeof(int) * 100;

new产生的原因：malloc/free无法满足动态对象的要求，来类中，对象在创建时需要自动执行构造函数，在消亡之前需要自动执行析构函数。由于malloc/free是库函数而不是操作符，不在编译器控制权限之内，不能把执行的构造函数和析构函数强加于malloc/free，所以有了new/delete。

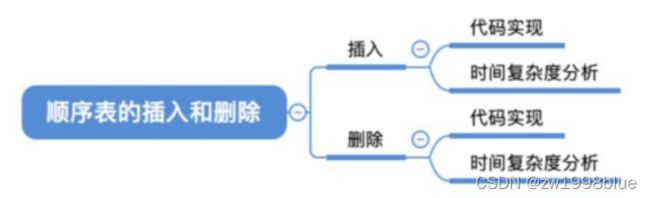
基本操作实现

插入

//插入：在线性表的第i个位置之前插入新的数据元素e，线性表的长度加1
int ListInsert(SqList *L, int i, ElemType e)
{
	if (i<1 || i>L->length + 1)	return -1;
	if (L->length >= MaxSize)	return -1;
	for (int j = L->length; j >= i; j--)
		L->elem[j] = L->elem[j-1];
	L->elem[i - 1] = e;
	L->length++;
	return 0;
}

时间复杂度：

---

删除

int ListDelete(SqList *L, int i,ElemType *e)
{
	if (i<1 || i>L->length) return -1;
	e = &L->elem[i - 1];//删除元素位置
	for (int j = i; j <= L->length; j++)//把第i个位置后的元素前移一位
		L->elem[j - 1] = L->elem[j];
	L->length--;
	return 0;
}

链表

我们怀着以下的几个问题来了解链式表示

链式存储的定义、各链表的基本操作和原理

单链表、双向链表、循环链表、静态链表的区别？

什么是头指针、头结点、首元结点？

---

链表包括单链表、双向链表、循环链表、静态链表

空间上，链式存储不需要使用地址连续的存储单元；因为额外存储指针，所以存储密度小于1,浪费空间。时间上，不同于顺序表的随机存取，链表是顺序存取，查找某元素需要通过头指针按顺序依次向后遍历查找；而删除和插入操作则不需要移动元素，只需改变指针的指向

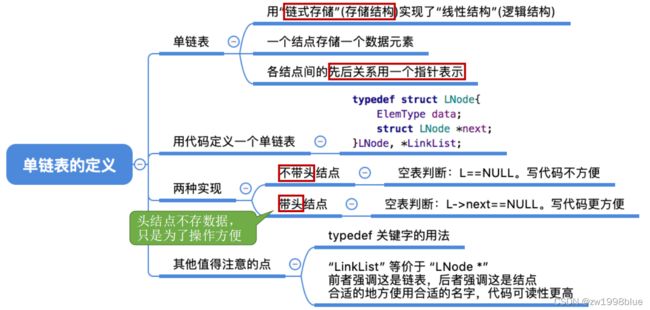
//单链表结点类型
typedef int ElemType;
typedef struct LNode
{
	ElemType data;
	struct Lnode *next;
}LNode,*LinkList;
//定义结点指针用LNode *p;定义链表用LinkList L;
但实际两者可以等同，因为结点和链表类型一样，写法不同只是用于区分它们，增强可读性

//双链表结点
typedef struct DNode
{
	ElemType data;
	struct Dnode *prior,*next;
}LDNode,*DLinkList;

//静态链表
typedef struct
{
	ElemType data;
	int next；
}SLinkList[MaxSize];

表示一个单链表，需要先设置一个头指针，这样就能找到链表中的 每个结点了。有时，为了操作方便，会给链表增加一个不存放数据的头结点（也可以存放表长等信息）。

头指针L：指向第一个结点的指针,常用于标识一个单链表L。

首元结点：存储第一个数据元素的结点

头结点：首元结点前的结点。好处有①便于首元结点的处理，使得对链表第一个位置的操作与其他位置一样，无需特殊处理。②无论链表是否为空，头指针都指向头结点的非空指针，便于空表和非空表统一处理

带头结点：L->next=NULL;        不带头结点：L=NULL；

单链表基本操作

1、建立单链表

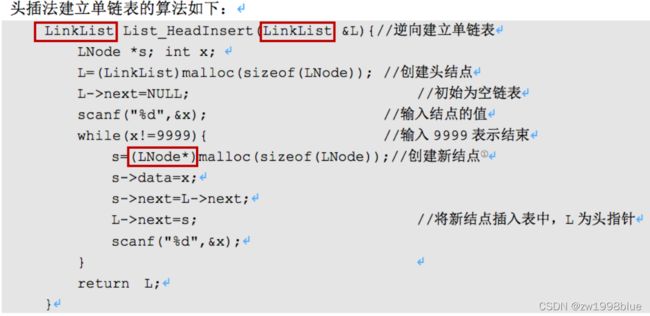
有头插法、尾插法。

头插法是每次把新节点插到头结点后面，使得其创建的单链表与数据输入顺序正好相反，称为逆序建表。尾插法是每次把新节点插到链表，使得其创建的单链表与数据输入顺序正好相反，称为正序建表。

注意：等号右边是某个结点，等号左边是某结点的指针域

头插法是先将头指针的后一节点赋给新节点的指针域，这样你就继承了头指针之后的一切，有了你的后继；第二步再把新节点赋给头指针的指针域，继承头指针，这样你就有了前驱，两者都有则完成插入。所以需要1个新结点s即可。

关键：s->next=L->next;        L->next=s;

修改指针的原则：先修改没有指针标记的那一端。因为一但先修改了L的指针域，L之后的结点就找不到了。

赋值操作前，每次都要创建新结点，分配一片内存空间，在把元素放入新结点中

尾插法每次要把新结点连接到链表尾部，所以要多设置一个指向表尾结点的尾指针。

操作分为三步：现将新结点s的指针域置空，有了后继；再把新结点赋值到尾结点r的指针域上，有了前驱；再让尾指针指向新的尾结点，为了后续结点的尾插

关键：s->next=NULL;        r->next=s;        r=s;//为了改变r指针的指向

LinkList List_TailInsert(LinkList &L) {
	LNode *r=L, *s;
	L = new LNode;
	int x = 5;
	s->data = x;
	while (x)
	{
		s = new LNode;//创建新结点
		s->next = r->next;
		r->next = s;
		r = s;
	}
}

---

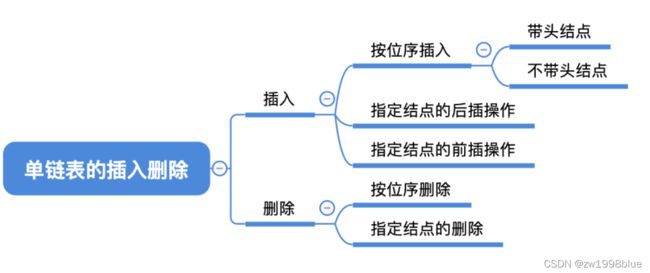
2、插入删除

 

插入

//实现插入
p=GetElem(L,i-1); 查找插入位置的前驱结点
s->next=p->next;
p->next=s;

 插入操作就是把值为x的结点插入到单链表的第i个位置，但是插入实际分为两种：

• 后插——就是按序号查找算法找到第i-1的结点，也就是待插入位置，然后进行插入。但是查找第i-1个元素使得时间复杂度为n；
• 前插——若在指定位置的之后插入，则不需要查找，时间复杂度是1。
• 转化方式：例如,s结点要插入到p结点之前，我们可以仍将s结点插在p结点之后，然后将s和p的数据互换，这样有满足逻辑关系，又使得时间复杂度为1

• s->next=p->next;
  p->next=s;
  swap(s->data,p->data);

删除

•  删除的通常做法是：从头结点按顺序找到待删除结点的前驱结点，然后删除，但是这里的遍历使得时间复杂度为n
• 改良做法：已知待删除结点p，可以选择把该节点和后继节点q的值交换，然后删除后继节点，可使得时间复杂度为1

	p = GetElem(L, i - 1);
	q = p->next;
	p->next = q->next;
	delete q;//删除q结点

3、应用

归并

双链表

产生原因：单链表只有一个指向后继的指针，如果要访问某节点的前驱结点，只能从头遍历，也就是访问后继节点的时间复杂度为1，访问前驱结点的时间复杂度为n。而引入双链表使得在插入、删除的时间复杂度只为1，缺点就是更加浪费空间。

循环链表

和单链表区别在于，最后一个结点的指针不是NULL，而是改为指向头结点。

优点是对表头和表尾进行操作的时间复杂度都是1.

静态链表

静态链表是借助数组来描述链式存储结构。

---

解题经验

链表的逆置、归并不需要额外空间，属于就地操作

快慢指针法：可以解决很多问题，如求链表中间结点、倒数第K个结点。   求中间结点时，快指针走两步慢指针走一步，当快指针走完时，慢指针刚好指向中间结点；查找倒数第k个结点时，慢指针不要动，快指针先走k-1步，然后两指针再以同样速度走。