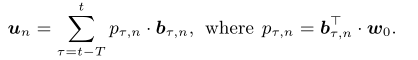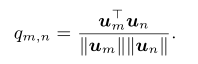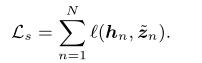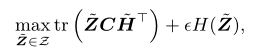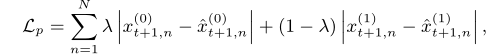ST-SSL:基于自监督学习的交通流预测模型
文章信息
文章题为“Spatio-Temporal Self-Supervised Learning for Traffic Flow Prediction”,是一篇发表于The Thirty-Seventh AAAI Conference on Artificial Intelligence (AAAI-23)的一篇论文。该论文主要针对交通流预测任务,结合自监督学习,衡量数据的时空异质性。
摘要
在智能交通系统中,准确预测不同时间段的城市交通流量是至关重要的。现有的方法存在两个关键的局限性:1、大多数模型集中预测所有区域的交通流量,而没有考虑空间异质性,即不同区域的交通流量分布可能存在偏差;2、现有模型无法捕捉时变交通模式引起的时间异质性,大多数现有模型通常是在所有时间段内与共享参数化空间进行时间相关性建模。为解决上述问题,文章提出了一种新的时空自监督学习(ST-SSL)的预测框架,该框架通过辅助的自监督学习范式,增强了交通模式表征,以反映时空异质性。具体而言,该模型构建在一个集成模块上,具有时间卷积和空间卷积。为实现自适应时空自监督学习,ST-SSL在属性层面和结构层面对交通流量图数据进行自适应增强。在增强的流量图的基础上,文章构建了两个基于自监督学习的辅助任务,通过时空异构感知增强对主要流量预测任务进行补充。文章的主要贡献如下:
该文章是第一个提出一种新的自监督学习框架来模拟交通流预测的时空异质性。所提出的预测框架可能会对其他实际的时空应用(例如空气质量预测)有所帮助。
文章提出了一种基于图结构时空图的自适应异构感知数据增强方案,以减弱噪声扰动对预测的影响。
文章引入两个自监督学习任务来补充主要的交通预测任务,通过增强模型识别能力和对交通时空异质性的认识。
基本概念
空间区域:文章将网络划分为N=I*J的网格,![]() 表示区域。
表示区域。
交通流量图(TFG):交通流量图定义为![]() ,其中V表示节点集合,为边集合,
,其中V表示节点集合,为边集合,![]() 为邻接矩阵,
为邻接矩阵,![]() 表示历史T个时间步交通网络内各个区域的流入量和流出量序列。
表示历史T个时间步交通网络内各个区域的流入量和流出量序列。
问题定义:给定若干历史时间步的交通流量图,文章所研究问题的目标是学习一个能够准确估计未来一个时间步内的所有区域的交通量的预测的函数。
模型框架
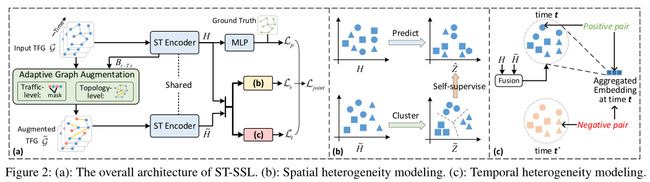
文章所提出的模型框架如下图中的图(a)所示。主要包括时空编码器(ST Encoder)、自适应图增广模块(Adaptive Graph Augmentation)。
时空编码器(ST Encoder):文章主要利用卷积神经网络构建时空编码器,将时间卷积分量与图卷积传播网络相结合,作为时空关系表示的主干。具体而言,时间特征提取层由基于门控机制的一维因果卷积构成,时间编码器沿时间维度进行卷积,如下式所示。
![]()
其中,![]() 表示第t个时间步交通网络的嵌入矩阵,
表示第t个时间步交通网络的嵌入矩阵,![]() 表示其中的第n行,即与区域
表示其中的第n行,即与区域![]() 相关,D表示嵌入维度。进一步,空间特征提取层如下式所示。
相关,D表示嵌入维度。进一步,空间特征提取层如下式所示。
![]()
文章的时空编码器采用“三明治”块结构构建,即以TC→SC→TC的顺序对数据进行处理。随着时空编码器的处理,时间维度最终变为0,从而得到最终的预测结果![]() 。
。
自适应图增广模块(Adaptive Graph Augmentation on TFG):文章设计了两阶段的图增广方法,即流量级数据增广和图拓扑级结构增广。首先,文章给出了不同区域异质性的衡量方法。具体而言,对于区域,其嵌入序列的计算方式如下。
其中,指权重![]() 不同时间步嵌入序列的聚合表示,
不同时间步嵌入序列的聚合表示,![]() 是可学习参数。该权重反映不同时间步与总流量规律的关系。基于上式,文章通过比对两个不同区域对应总流量规律的差异,从而反映不同区域的异质性。具体如下式所示,该值越大,则两个区域之间的相关性越强,因此异质性越小。
是可学习参数。该权重反映不同时间步与总流量规律的关系。基于上式,文章通过比对两个不同区域对应总流量规律的差异,从而反映不同区域的异质性。具体如下式所示,该值越大,则两个区域之间的相关性越强,因此异质性越小。
基于上式,文章提出流量级数据增广和图拓扑级结构增广。具体而言,流量级数据增广旨在基于概率掩盖第个时间步中相关性较弱的流量,其中服从二项分布![]() ,其处理结果为
,其处理结果为![]() 。图拓扑级结构增广旨在对网络内所有区域进行分析,包括两个步骤:1、若两个区域的流量规律不是高度相关,即异质性较大,基于概率掩盖这两个区域之间的连接,服从二项分布
。图拓扑级结构增广旨在对网络内所有区域进行分析,包括两个步骤:1、若两个区域的流量规律不是高度相关,即异质性较大,基于概率掩盖这两个区域之间的连接,服从二项分布![]() ;2、若两个区域之间的流量规律异质性较小,则会依照服从二项分布
;2、若两个区域之间的流量规律异质性较小,则会依照服从二项分布![]() 的概率添加一条边。基于上述两阶段数据增广,得到新的TFG,如下所示。
的概率添加一条边。基于上述两阶段数据增广,得到新的TFG,如下所示。
基于自监督学习的空间异质性建模:给定经过增广的TFG,文章的目标是使区域嵌入在辅助自监督信号的情况下有效地保持空间异质性。为实现该目标,文章在区域级别上设计了一个基于软聚类的自监督学习任务,将区域映射到对应于不同城市区域功能的多个潜在表示空间。具体而言,文章生成K个聚类嵌入![]() 。聚类过程如下式所示。
。聚类过程如下式所示。
![]()
其中,为D维向量,表示区域的区域嵌入。基于上式,区域的聚类指派如下。
![]()
为生成自监督学习的特征,所设计的辅助任务旨在预测用于原始区域嵌入生成的区域指派![]() 。对于区域,对应的自监督学习的损失计算方法如下所示。
。对于区域,对应的自监督学习的损失计算方法如下所示。
对于所有区域而言,其损失计算如下。
上述聚类方法存在两方面问题:首先,生成的聚类指派矩阵是由聚沉成绩所产生的,每个区域的聚类指派求和可能不为1;其次,可能存在每个区域都有相同的分配。为解决上述我呢提,文章提出区域聚类的分布正则化。具体而言,文章采用最大熵原理,即![]() ,定义可行解所构成的集合如下。
,定义可行解所构成的集合如下。
对于每一个可行的聚类指派,可以将嵌入矩阵![]() 映射为聚类矩阵
映射为聚类矩阵![]() 。因此搜索可以通过最大化嵌入矩阵和聚类的相似度获得最优解,如下式所示。
。因此搜索可以通过最大化嵌入矩阵和聚类的相似度获得最优解,如下式所示。
其中,tr()表示矩阵的迹,![]() 表示熵函数,计算公式如下。
表示熵函数,计算公式如下。
![]()
基于自监督学习的时间异质性建模:文章进一步设计了一个自监督学习任务,通过强制时间步长特定的流量模式表示之间的差异,将时间异质性注入到时间感知区域嵌入中。具体而言,文章首先融合原始的TFG和增广后的TFG。
进一步,将不同区域的特征聚合,从而获得第t个时间步网络级表示,计算方式如下。
为增强不同时间步表示的辨别能力,文章将网络级表示和区域级表示作为嵌入对![]() ,其中若区域级表示和网络级表示为同一个时间步则为正值,反之,则为负值。最后,基于上述定义,时间异质性建模的损失函数为交叉熵损失函数,定义如下。
,其中若区域级表示和网络级表示为同一个时间步则为正值,反之,则为负值。最后,基于上述定义,时间异质性建模的损失函数为交叉熵损失函数,定义如下。
综上所述,模型的整体损失函数定义如下:
实验
文章在几个真实数据集上进行一系列实验,以评估ST-SSL的性能。数据集包括纽约Bike数据集和Taxi数据集,以及北京出租车数据集。这些实验旨在回答以下研究问题:
问题1:与各种基线相比,ST-SSL的整体流量预测性能如何?
问题2:设计的不同子模块对模型性能的贡献是什么?
问题3:对于异构空间区域和不同时间段,ST-SSL的性能如何
问题4:增广图和学习表征如何使模型受益?
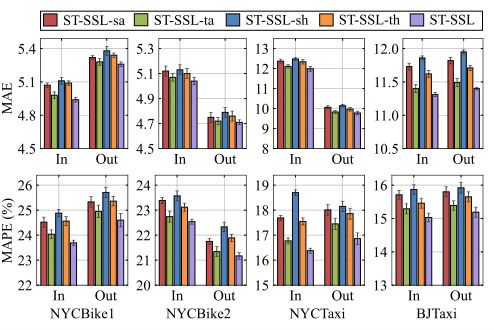
问题1:在不同数据集上的实验结果如下图所示。可以看到ST-SSL的预测误差最低。
进一步,文章对所提出模型在不同区域的预测误差进行可视化,并比对了不同基线模型的预测误差,如下图所示。
问题2:为验证所提出模型不同子模块的影响,文章构建了四组模型的变体进行消融实验。具体而言,ST-SSL-sa表示该模型用随机边缘去除和增加的方式取代了图拓扑上的异构引导结构增广;ST-SSL-ta表示该模型使用随机交通量掩膜替换原有的基于异质性引导的流量增广;ST-SSL-sh表示该模型不使用空间异质建模模块;ST-SSL-th表示该模型不使用时间异质性建模模块。实验结果如下。
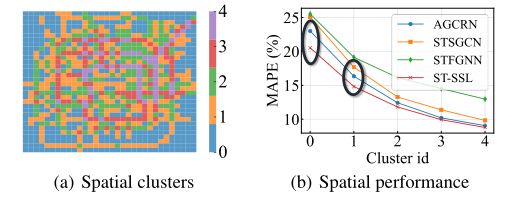
问题3:为探究ST-SSL的鲁棒性,文章在北京出租车数据集上对具有异构数据分布的空间区域和具有不同模式的时间段进行了流量预测。对于空间异质性而言,文章利用历史交通数据的统计量,例如均值、中位数、标准差,将不同区域进行聚类。下图分别展示了不同区域的划分结果以及预测结果。
对于时间异质性而言,文章将工作日分为四个时段,将节假日分为2各时段。下图分别展示了划分方法和预测结果。
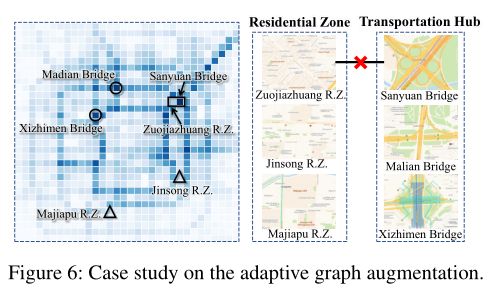
问题4:文章通过定性分析的方法进行分析,在北京出租车数据集上进行实验。结果如下图所示。文章所提出的方法自适应地去除了具有异构交通模式的相邻区域之间的连接。同时,在城市潜在功能相似的遥远区域之间建立联系。通过这种方式,ST-SSL不仅可以消除低相互关联交通模式的区域连接,还可以捕获全球城市背景下的长期区域依赖关系
此外,为了进一步探究ST-SSL中的嵌入是如何提升预测精度的,文章对比了AGCRN和ST-SSL的预测结果,通过T-SNE方法进行可视化,如下图所示。
结论
文章提出一种新的时空自监督学习(ST-SSL)框架以解决交通预测问题。具体而言,文章整合了时间和空间卷积来编码时空交通模式。进一步,文章设计两个主要模块:1、一个由自适应图增强和基于聚类的生成任务组成的空间自监督学习范式;2、一个依赖于时间感知的对比任务的时间自监督学习范式,以空间和时间异质性感知的自监督信号补充主要的交通流量预测任务。在4个交通流数据集上的综合实验证明了ST-SSL算法的鲁棒性。