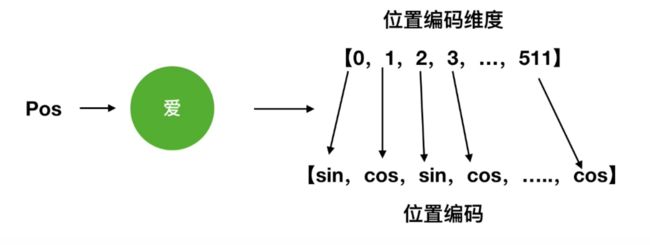
Transformer 中 Positional Encoding 实现
参考博文:
https://www.cnblogs.com/nickchen121/p/16470736.html
解决问题
位置编码的主要目的是确保模型能够理解序列中的元素之间的相对位置和顺序,从而更好地捕捉到语义信息。在Transformer模型中,位置编码通常与词嵌入(word embeddings)相加,以形成模型的输入表示。这有助于模型在处理序列数据时更好地理解元素的位置和顺序,从而提高其性能,特别是在自然语言处理任务中。
原理
这里就是拿经典款transformer举例了
这个i是维度,2i这块是告诉你是sin还是cos的,是0~dimension/2
详细过程:
sin(pos+k) = sin(pos)*cos(k)+cos(pos)*sin(k) #sin表示偶数维度
cos(pos+k) = cos(pos)cos(k) +sin(pos)sin(k) #cos表示奇数维度
!pos+k可是pos和k的线性组合!
例如
pos+K=5, 当我计算第五个单词的位置编码时:
pos=1, k=4; pos=2, k=3;
这样就可以得知几个位置之间的相对关系
代码实现
Transformer
一维绝对的位置编码
def create_1d_absolute_sincos_embeddings(n_pos_vec,dim):
assert dim % 2 == 0, "wrong dimension" # dim must be even
# 初始化position embedding
position_embedding = torch.zeros(n_pos_vec.numel(), dim, dtype=torch.float) #numel()返回数组元素个数
# omega是对i进行遍历
omega = torch.arange(dim//2, dtype=torch.float) #//是整除
omega /= dim/2.
omega = 1./(10000**omega)
out = n_pos_vec[:, None]@omega[None, :] # 先把n_pos_vec变成列向量,一个维度加上None相当于扩了一维;接下来是把omega拓成一个行向量, @是矩阵乘法
emb_sin = torch.sin(out)
emb_cos = torch.cos(out)
# 接下来是偶数位用sin赋值,奇数位用cos去赋值
position_embedding[:, 0::2] = emb_sin
position_embedding[:, 1::2] = emb_cos
return position_embedding
if __name__ == '__main__':
n_pos = 4
dim = 4
n_pos_vec = torch.arange(n_pos, dtype=torch.float)
print(n_pos_vec)
pe = create_1d_absolute_sincos_embeddings(n_pos_vec,dim)
print("pe", pe)Vision Transformer
一维的,绝对的,可训练的
这里用的也是一维的位置编码因为论文里做了实验表明二维的位置编码对模型效果并没有提升
def create_1d_absolute_trainable_embeddings(n_pos_vec,dim):
# 传入索引
# n_pos_vec: torch.aramge(n_pos, dtype=torch.float)
# 因为可学习所以用nn.embedding来实现
position_embedding = nn.Embedding(n_pos_vec.numel(), dim)
# 初始化weight(parameter class)
nn.init.constant_(position_embedding.weight, 0.)
return position_embedding # 一维的,绝对的,可学习的embeddingSwin Transformer
二维的,相对的,基于位置偏差的
相对位置,可学习
def create_2d_relative_bias_trainable_embeddings(n_head,height,width,dim):
# embeddings的行数就是bias的个数,列数就是num_heads
# 横轴取值 width:5[0,1,2,3,4] bias ={-width+1, width-1 }{-4,4} 4-(-4)+1 = 9
# 纵轴取值 height:5[0,1,2,3,4] bias ={-height+1, height-1} 1-(-1)+1 = 3
position_embedding = nn.Embedding((2*width-1)*(2*height-1), n_head)
# 初始化weight(parameter class)
nn.init.constant_(position_embedding.weight, 0.)
# 获取window中二维的,两两之间的位置偏差
# step1:算出横轴和纵轴各自的位置偏差,用网格法把横轴的位置索引和纵轴的位置索引定义出来
def get_2d_relative_position_index(height, width):
m1, m2 = torch.meshgrid(torch.arange(height), torch.arange(width)) # m1行一样,m2列一样
coords = torch.stack([m1, m2]) # 把m1和m2拼接起来,dim=-1表示最后一个维度 #2*height*width
coords_flatten = torch.flatten(coords,1) # 把coords压缩成一维,dim=1表示第一个维度,得到2*【height*width】
ralative_coords_bias = coords_flatten[:, :, :None]- coords_flatten[:, None, :]#得到网格里任意两点横轴纵轴坐标的差值,[2,height*width,height*width]
# 把它们都变成正数
ralative_coords_bias[0, :, :] += height-1 # 横轴坐标的差值,0代表高度维
ralative_coords_bias[1, :, :] += width-1 # 纵轴坐标的差值 1代表宽度维
# 把两个方向上的坐标转化成一个方向上的坐标,类似于把一个2dtensor赋值到1dtensor
# A;2d,B:1d B[i*cols+j] = A[i,j]
ralative_coords_bias[0,:,:] += ralative_coords_bias[1, :, :].max()+1 # 把横轴坐标的差值转化成一维坐标,即i*cols
# 相对位置索引
return ralative_coords_bias.sum(0) # [height*width,height*width] # 两个方向上的坐标相加,得到相对位置索引
relative_position_bias = get_2d_relative_position_index(height, width) # [height*width,height*width]
bias_embedding = position_embedding(torch.flatten(relative_position_bias)).reshape(height*width,height*width,n_head) # [height*width,height*width,n_head]
bias_embedding.permute(2,0,1).unsqueeze(0) # [1, n_head,height*width,height*width]
return bias_embedding # 二维的,相对的,可学习的embedding