带你彻底了解红黑树与AVL树(详细)
红黑树介绍
红黑树,一种二叉查找树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black。
通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出俩倍,因而是接近平衡的。
红黑树,作为一棵二叉查找树,满足二叉查找树的一般性质。下面,来了解下二叉查找树的一般性质。
二叉查找树,也称有序二叉树(ordered binary tree),或已排序二叉树(sorted binary tree),是指一棵空树或者具有下列性质的二叉树:
若任意节点的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
若任意节点的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
任意节点的左、右子树也分别为二叉查找树。
没有键值相等的节点(no duplicate nodes)。
因为一棵由n个结点随机构造的二叉查找树的高度为lgn,所以顺理成章,二叉查找树的一般操作的执行时间为O(lgn)。但二叉查找树若退化成了一棵具有n个结点的线性链后,则这些操作最坏情况运行时间为O(n)。
红黑树虽然本质上是一棵二叉查找树,但它在二叉查找树的基础上增加了着色和相关的性质使得红黑树相对平衡,从而保证了红黑树的查找、插入、删除的时间复杂度最坏为O(log n)。
但它是如何保证一棵n个结点的红黑树的高度始终保持在logn的呢?这就引出了红黑树的5个性质:
每个结点要么是红的要么是黑的。
根结点是黑的。
每个叶结点(叶结点即指树尾端NIL指针或NULL结点)都是黑的。
如果一个结点是红的,那么它的两个儿子都是黑的。
对于任意结点而言,其到叶结点树尾端NIL指针的每条路径都包含相同数目的黑结点。
正是红黑树的这5条性质,使一棵n个结点的红黑树始终保持了logn的高度(红黑树的高度至多为2log(n+1)证明略),从而也就解释了上面所说的“红黑树的查找、插入、删除的时间复杂度最坏为O(log n)”这一结论成立的原因。
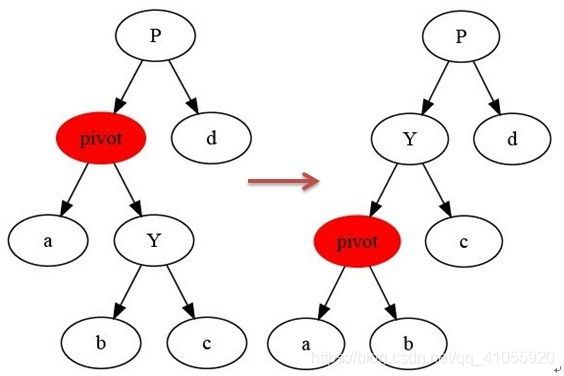
_第1张图片](http://img.e-com-net.com/image/info8/7e8ccfc1c0114bf1b5ead460bb1724f8.jpg) 左旋
左旋
AVL树
概念:
AVL树又称为高度平衡的二叉搜索树。它能保持二叉树的高度平衡,尽量降低二叉树的高度,减少树的平均搜索长度。
性质:
左子树和右子树的高度之差绝对值不超过1。
树中的每个左子树和右子树都是AVL树。
每一个节点都有一个平衡因子,任一节点的平衡因子是1、0、-1,平衡因子等于右子树的高度减去左子树的高度。
AVL树的调整
如果在AVL树中进行插入或删除节点后,可能导致AVL树失去平衡。这种不平衡可能出现在下面四种情况中:
对a的左儿子的左子树进行一次插入。(LL)
对a的左儿子的右子树进行一次插入。(LR)
对a的右儿子的左子树进行一次插入。(RL)
对a的右儿子的右子树进行一次插入。(RR) 其中1、4是关于a点的镜像对称,2、3是关于a点的镜像对称。
第一种情况(1、4)需要通过对树的一次单旋转完成调整。 第二种情况(2、3)需要通过对树的一次双旋转完成调整。
下面展示一些 内联代码片。
//右单旋
private AVLTreeNode<T> rightRotation(AVLTreeNode<T> node) {
AVLTreeNode<T> left = node.left;
node.left = left.right;
left.right = node;
// 更新高度
node.height = Math.max(height(node.left), height(node.right)) + 1;
left.height = Math.max(height(left.left), height(left.right)) + 1;
return left;
}
//左单旋
private AVLTreeNode<T> leftRotation(AVLTreeNode<T> node) {
AVLTreeNode<T> right = node.right;
node.right = right.left;
right.left = node;
// 更新高度
node.height = Math.max(height(node.left), height(node.right)) + 1;
right.height = Math.max(height(right.left), height(right.right)) + 1;
return right;
}
* 先右旋后左旋
*
* @param node 失衡树根节点
* @return 旋转后的根节点
*/
private AVLTreeNode<T> rightLeftRotation(AVLTreeNode<T> node) {
node.right = rightRoation(node.right);
return leftRoation(node);
}
* 先左旋后右旋
*
* @param node 失衡树根节点
* @return 旋转后的根节点
*
private AVLTreeNode<T> leftRightRotation(AVLTreeNode<T> node) {
node.left = leftRoation(node.left);
return rightLeftRoation(node);
}
红黑树与AVL树的区别
红黑树旋转操作非常局部化,而且次数极少(插入最多两次旋转,删除最多三次旋转),而改变颜色的操作不会影响到用户对树的query操作(即不要lock),另外很多树,如AVL树,2-3树,2-4树都可以转化成红黑树,红黑树能达到O(logn)高度,但是不像AVL树那样严格要求左右子树高度差必需相差不超过1。可以说RB树是目前为止高度要求最灵活的准平衡BST。准平衡是相对完全二叉树来说的,AVL树(比如Fibonacci树)也不是完美平衡的。
红黑树的算法时间复杂度和AVL相同,但统计性能比AVL树更高。
当然,红黑树并不适应所有应用树的领域。如果数据基本上是静态的,那么让他们待在他们能够插入,并且不影响平衡的地方会具有更好的性能。如果数据完全是静态的,做一个哈希表,性能可能会更好一些。
红黑树是一个更高效的检索二叉树,因此常常用来实现关联数组(“关联数组”是一种具有特殊索引方式的数组。不仅可以通过整数来索引它,还可以使用字符串或者其他类型的值(除了NULL)来索引它。)。