快速排序，归并排序，希尔排序，堆排序（讲解及C++实现）

此文章算是我用了一天多的时间对数据排序算法的一次小结，算是复习一下排序算法，顺便扫清一些以前没有看过的排序算法部分。这个文章有比较详细明了的讲解和总结（其实大多都是从其他的文章参考到的），也供一起学习使用。里面的代码是自己实现的，可能性能不是很优化。 受作者水平所限，如果代码有任何问题，请在评论区提出。

首先说一些比较基本的排序算法

比较基础的排序算法包括冒泡排序，选择排序，和插入排序方法， 这三种排序方法比较简答，其代码实现也很容易，仅在下面简单提及：

1. 对于冒泡排序算法，每一次将小的进行前移或者将大的向后移动(不详细说)，时间复杂度为$n+n-1+...=\frac{n(n+1)}{2}$ 即为$O(n^2)$
2. 选择排序是每一次找出最大的数将其与第一个交换，则每一次进行寻找就可以了，时间复杂度仍然为$O(n^2)$
3. 插入排序是将记录插入到已经排好序的序列中, 从而得到一个新的有序序列的过程。其时间复杂度仍然为$O(n^2)$, 其思路是先认为第一个数据是有序的，然后对于所有后面的数据(例如数据$a$)，寻找第一个小于数据$a$的元素，并且将这个数据插入到该元素的后面，这个实现也较为简单，代码可以参考六大排序算法：插入排序、希尔排序、选择排序、冒泡排序、堆排序、快速排序

而本文主要讲解四种排序算法，即快速排序，归并排序，希尔排序和堆排序算法

一、快速排序算法

快速排序算法是对冒泡排序算法的一种改进， 其思路是首先以随机的一个数(排序中可以使用数组第一个数) 作为基准数，然后对数组的两边先进行整理， 使得基准数能够插入到一个位置并通过交换使得左边的数

快速排序方法是从数组的两端开始进行探测的， 即在数组的两端分别定义一个下标$i,j$,以如下的数组为例，首先，下标j从右向左进行移动并找到第一个比基准数小的数，然后下标i开始从左向右移动并找到第一个比i小的数，找到之后，将两个数进行交换，则最终左边的数都会比基准数小，而右边的比基准数大

最终，当下标i和j移动到同一个数时，则左边的数据均为比原基准数小的数据，而右边的均为比原基准数大的数据。
由于是下标 $j$先进行移动的，总是找到一个比基准数小的数，而 i 移动到和 j 相遇时, 显然相遇处的数是比基准数小的数，

数据	49	1	3	52	75	13	8	9	12	17	63	76	81
下标	i												j

下标i,j分别找到比基准数小和基准数大的数

数据	49	1	3	52	75	13	8	9	12	17	63	76	81
下标				i						j

然后将 $i,j$对应的数进行交换，

数据	49	1	3	17	75	13	8	9	12	52	63	76	81
下标				i						j

排好序的每一边的数组先调换12和75，相遇时，首先 $j$ 找到9为比原来数小的数，最终i,j在9 处相遇

数据	49	1	3	17	12	13	8	9	75	52	63	76	81
下标								i,j

接着只需要交换49和9即可得到符合要求的数组，如此进行递归，可以分别排好两边即可

快速排序每一次排序需要遍历n个元素并且调换位置， 而递归的深度为${\log }_{2}n$, 此时则其算法的总的复杂度为$O(n{\log }_{2}n)$， 而其中只需要一个辅助的参数来进行数组元素的调换，以及一个temp来存储对应的基准数，空间复杂度为$O(1)$

这里需要补充说明的是，首先下面这个代码是我修改过两次的，修复了在数字相等时进行排序的栈的溢出和不能排序的问题

另外需要说明，快速排序的最坏情况是逆序数组情况, 这里放上一道用来测试的例题:

上面的题目如果直接使用下面的快速排序代码是会超时的，而希尔排序和归并排序都是可以通过的

class Solution {
    public:
        bool containsDuplicate(vector nums) {
            int n = nums.size();
            if (n<=1) return false;

            int* nums2 = (int*)malloc(n*sizeof(int));
            for (int i = 0; i < n; i++) *(nums2 + i) = nums[i];

            Quick_Sort(nums2, n); // 快速排序，如果想测试其他的，只要改用其他入口函数并复制粘贴私有函数即可
            for (int i = 0; i < n-1; i++){
                if (nums2[i] == nums2[i+1]) return true;
            }
            return false;
        }
};

超时并提示最后一次测试数据为：[-24500,-24499,-24498,-24497,-24496,.....
这是由于，在数组逆序排列的情况下，每一次j都会由于找不到比其小的数重新调用函数,造成了大量的时间浪费

快速排序的cpp代码实现:

#include
#include
using namespace std;

void Show_Array(int A[], int length) {
	for (int i = 0; i < length; i++) {
		cout << A[i] << " ";
	}
	cout << endl;
}


// 快速排序迭代函数
void Sort_Arr_quick(int A[], int start, int end) {
	if (end - start > 1) { // 对于序列长度至少为3的情形, 
		// 先行排好序，再对子数列进行排序
		int i = start + 1, j = end, temp = A[start]; // temp 为标准数

		for (; j > start ; j--) {
			// 如果找到了最小的数
			if (A[j] <= temp) {
				// 当右端的下标j找到比标准数小的数时,i从左端出发 
				// 注意: 小于等于时，应该放在左边，也要交换
				for (; i < j; i++) {
					if (A[i] > temp) { // 此时，找到了大的数,则进行交换
						int t = A[i];
						A[i] = A[j];
						A[j] = t;
						break; // ******注意******* 放到外循环中，j继续向左移动
					}
				} // 退出循环之后，有i = j,且得到在i = j上的数比基准数小，此时直接进行交换

				if (i == j) { // 两个下标碰面之后
					if (i == end) {
						// 对于(1,1,1,1,1,1)的情况，j最终抵达1,直接再次循环 ,此时可能会导致栈溢出的现象
						// 此时i已经达到最右侧，说明最大的数就是这个数, 而j处的可能是这个数，也可能比这个小
						// 此时可能是两端都是i中间小的情况, 则和i-1交换数值,
						// 需要从i-1再次排序
						if (A[j] < temp) {
							A[start] = A[i];
							A[i] = temp; // 交换，之后对中间的部分排序,不用分别排序
							Sort_Arr_quick(A, start, end);
						}
						else if (A[j] == temp){
							A[start] = A[i - 1];
							A[i - 1] = temp; // 交换倒数第二个数
							Sort_Arr_quick(A,start, end-1); // 丢弃最后一个数，内部继续排序 
						}
					}
					else { // 交换左右侧的数
						A[start] = A[i];
						A[i] = temp;   // 交换两数
						Sort_Arr_quick(A, start, i);     // 此时i最小可以达到0,而数组最大下标至少为2
						Sort_Arr_quick(A, i + 1, end);	 // 两个部分分别sort
					}
					break;
				}
			}
		}
		// 如果start达到数组首端，则没有搜索出比temp小的数，此时即可直接返回
		if (j == start) {
			// 此时，i达到最左边，说明start是数组中最小的数，则只需要丢弃第一个数，继续排序
			Sort_Arr_quick(A, start + 1, end);
			// Sort_Arr_quick(A, start + 1, end);
		}
	}
	else { // 数组的长度此时小于等于2, 则直接进行交换
		if (A[end] < A[start]) {
			int t = A[end];
			A[end] = A[start];
			A[start] = t;
		}
	}
}

// 快速排序入口函数
void Quick_Sort(int A[], int length) {
	if (length == 1) return; // 直接结束函数 
	Sort_Arr_quick(A, 0, length - 1);
}

// 快速排序算法
int main() {
	int length = 12;
	int A[12] = {170,-368,148,672,397,-629,-788,192,170,309,-615,-237 };
	Quick_Sort(A, length);
	Show_Array(A, length);
	return 0;
}

二、归并排序算法

使用归并的排序算法的思路是将排序问题进行分治算法，使用递归或者迭代的算法将数组拆分为子数组，并将子数组得到的部分进行继续拆分，直到无法拆分时，将得到的结果进行组合，可以参考这篇文章 (下图和讲解均出自这篇文章)

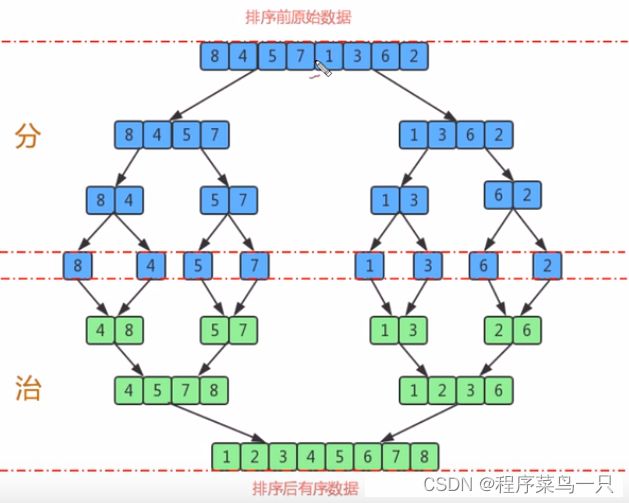
归并排序的主要思路是拆分与合并

首先给出一个有start, mid和end的排序函数 sort_arr用于数组的拆分，如果数组长度大于2,则继续使用回调拆分数组

而数组的排序是在合并过程中进行的，合并过程中，需要准备一个Temp数组，利用sort_arr函数给出的组合区段的start，end和mid值，将start和end区段内的部分以mid剖开并视为两个数组，每一次取两数组中首元素较大的一个放入Temp数组中

在拆分的部分，通过$n$次递归可以递归出$2^n$个数据，故递归深度为$lo{g}_{2}n$。Temp数组中，每一次比较两个有序数组中首元素的大小，每一层排完的时间复杂度为$n$, 而两个数组中的首元素大小分别进行排序，算法的总的时间复杂度为 $O(n\times lo{g}_{2}n)$ ，而最终需要一个辅助数组来进行存储得到的数据，则其空间复杂度为$O(n)$。

故归并排序的算法时间复杂度为$O(n\times {\log }_{2}n)$, 是一种较为优越的排序算法，cpp 代码实现如下 :

# include 
# include 
# include 

using namespace std;

void Show_Array(int A[], int length){
	for (int i = 0; i < length; i++) {
		cout << A[i] << " ";
	}
	cout << endl;
}

// 融合数组的两个部分
void Merge_Array(int A[], int tempArr[], int start, int mid, int end){
	int i = start;
	int j = mid + 1; // 第二个部分的起始下标
	int index = start;
	// 注意: i == mid时，进行终止, 并需要判断 i,j 和mid以及数组length之间的关系，否则会导致数组溢出现象
	while (index <= end)
	{	// 注意: 不是i每一次都要进行自增，是将小的数放在Temp数组中之后，则将i或者j进行自增运算
		if (i <= mid && j <= end) {
			if (A[i] < A[j]) {
				tempArr[index] = A[i++];
				index++; 
				// 事先进行取值，之后进行自增运算
			}
			else {
				tempArr[index] = A[j++];
				index++;
			}
		}
		else if (i > mid){
			tempArr[index] = A[j++];
			index++;
		}
		else if (j > end){
			tempArr[index] = A[i++];
			index++;
		}
	}
	// 注意: 由于归并排序使用的是已经排好序的数组，应当是Temp而不是A,因此要将Temp中排好的序重新赋值给A;
	for (int i2 = start; i2 <= end; i2++) {
		A[i2] = tempArr[i2]; 
	}
}

// 归并排序函数 --> 这个是用来拆分的部分
void sort_arr(int A[], int tempArr[], int start, int end) { 
	// 注意第二个数组指针可以直接进行数组参数的书写
	// 这个函数是用来递归寻找中间点的函数
	if (start < end)  // 如果仅有1个元素, 则不进行处理，不使用递归
	{
		int mid = start + (end - start) / 2;
		// 其中, 由于是整数运算，自动丢弃小数部分
		// 其中，如果使用 (start + end) /2 , 可能会导致整数溢出，因此使用上述算式
		sort_arr(A, tempArr, start, mid);
		sort_arr(A, tempArr, mid + 1, end);
		Merge_Array(A, tempArr, start, mid, end);
		// 每一次Merge的部分，都从start -> mid, mid -> end 排好序了
		// 最终排序的递归到 1x1 的部分
		// 将两个部分进行排序后重新放回tempArr中
	}
}

// 归并函数主函数
void Merge_Sort(int A[],int length) {  
	// 直接修改数组元素内的值
	int *p;
	p = (int*)malloc(length * sizeof(int)); // 分配大小为length的辅助数组p 
	// p = (int*)calloc(length, sizeof(int));  
	if (p)
	{
		// 检测是否辅助数组分配成功
		sort_arr(A, p, 0, length - 1);
		free(p);   // 释放指针空间, 在调用成功之后，
	}
	else
	{
		cerr << "Error : failed to allocate the memory" << endl;
	}
}

int main() {
	// 归并排序算法
	int A[13] = { 1, 49, 3, 52, 75, 13, 8, 9, 12, 17, 63, 76, 81 };
	// 使用递归或者迭代的算法，将归并排序采用二叉树来进行实现 ，递归的深度为log2n
	// 每一次，将递归得到的两个数组再次进行递归拆分，直到无法拆分时，进行排序并将结果合并为一个数组, 
	// 合并之后, 得到的结果再次和相邻的部分进行合并，即从二叉树底端再次合并到顶端
	int length = 13;
	Merge_Sort(A, length);  
	Show_Array(A, length);
	return 0;
}

三、希尔排序算法

附注：如果要了解希尔排序，首先应当会插入排序，如果没有基础可以参考C++算法之插入排序。 另外说明一下本文代码中的插入排序思路和上文中逐步交换的并非一致，本文中的插入排序是从后向前搜索并插入到第一个比原数据大的数据之后。如果没有搜索到，就放在数组最前面，首先记录数据点（拿出来需要插入的点这里称为数据点）的值，然后从数据点要插入点的下标到数据点的原先下标部分的数据，整体向后移动一格给插入腾出空间，之后进行数据的插入赋值。

希尔排序方法是插入排序方法的改进， 希尔排序的原理是利用插入排序在数组越有序的情况下，插入运算的次数越少这一特性， 先对数组数据进行分组后插入排序整理，使得最后一次插入排序的运算量减少的排序方法。

希尔排序在最坏的情况下复杂度仍然为$O(n^2)$, 但实际运行效率较高，往往我们可以使用$O(n^{1.3})$来估计数组的效率

希尔排序的基本思路是先选择一个整数作为增量，将待排序的文件中的所有数据进行分组，并以分出来的每个等差数列作为一组，再次排序

我们仍然使用快速排序用到的长度为13的数组作为示例

数据	49	1	3	52	75	13	8	9	12	17	63	76	81

此时，假设我们想要将数据分为三组，我们取3作为数组的增量，则得到的三个子数组如下：

第一组	49	52	8	17	81
第二组	1	75	9	63
第三组	3	13	12	76

此时，对每一组分别进行插入排序得到如下数组

第一组	8	17	49	52	81
第二组	1	9	63	75
第三组	3	12	13	76

第一次整理之后，得到的数组为：

8	1	3	17	9	12	49	63	13	52	75	76	81

第二次使用2为步长进行分组再次插入排序整理

第一组	8	3	9	49	13	75	81
第二组	1	17	12	63	52	76

排序后:

第一组	3	8	9	13	49	75	81
第二组	1	12	17	52	63	76

则第二次整理之后，数组变为

3	1	8	12	9	17	13	52	49	63	75	76	81

此时可以发现有序了很多，最后一次整体再次使用插入排序，其运算量相比直接插入排序也会少了很多。

另外需要注意的是，其中，每一次排序的选取的间隔(代码中记为$space$) 不同，可能导致不同的结果。其中选取n的方法往往可以使用Knuth提出的$gap=gap/3+1$的方法来进行, 具体可以参考【排序算法】希尔排序（C语言）

代码如下：

#include 
#include 
using namespace std;

void Show_Array(int A[], int length) {
	for (int i = 0; i < length; i++) {
		cout << A[i] << " ";
	}
	cout << endl;
}

// 以指定的间隔进行分组并排序
void sort_Arr_shell(int Arr[], int length, int space) {
	for (int init_index = 0; init_index < space; init_index++) { // init_index最多达到space
		// 尝试在space之内的所有的初始index值
		// 进行区间内的插入排序
		for (int st = init_index + space; st < length ; st += space){ // 第一次st应该是5
			// 记录插入排序的交换数字下标为st, 并使用st向前搜索需要插入的位置
			
			int i = st - space;
			for ( ; i >= init_index; i -= space) {
				if (Arr[i] < Arr[st]) {
					int temp = Arr[st];
					for (int k = 0 ; st - k * space > i; k++) {
						// 从 i * space 开始到st位置,整体向后赋值移动一格(如果没有，取消操作,终止循环)
						Arr[st - k * space] = Arr[st - (k + 1) * space];  // 赋值到i+2 * space为止
						// 注意要使用从后向前赋值的方式进行后移
					}
					Arr[i + space] = temp; // 将st处的值插入到Arr的i+space对应位置
					break;
				}

			}

			// 此时将数据插入到Arr[init_index+space * i上]
			if (i < init_index) { // 此时应当有 i < 0
				// 如果成功循环完毕后, 发现i比init_index小(对应于init_index - space),
				// 此情况时Arr[st]是最小的数的情况，此时用temp存储并将st，并将前方整体后移一格
				int temp = Arr[st]; 
				for (int k = 0; st - k * space > init_index; k++) {
					// 从 i + 2* space 开始到st位置(如果没有，取消操作,终止循环),整体向后移动一格
					// 注意: init_index 也需要赋值到 init_index + space中
					Arr[st - k * space] = Arr[st - (k + 1) * space]; 
				}
				Arr[init_index] = temp; // 将st处的值插入到Arr的i+space对应位置
			}
		}
	}
}

// 希尔排序入口函数
void Shell_Sort(int Arr[], int length) {
	int space = length; // 使用length/3 +1获取下一步的增量
	do {
		space = space / 3 + 1;
		sort_Arr_shell(Arr, length, space); 	
	} while (space != 1); // 最后一次的space是1
	// 每一次更新init_space
}

// 希尔排序算法
int main(){
	int A[13] = { 52,1, 81, 49,75, 13, 8, 9, 12, 17, 63, 76, 3 };
	int length = 13; 

	Shell_Sort(A, length);
	Show_Array(A, length);
	return 0;
}

四、堆排序算法

堆排序算法是依据树形结构来进行的
堆是一种称为完全二叉树的结构

首先我们介绍大根堆和小根堆

其中大根堆的结构是根顶部(父节点)比底部(两个子节点)数字均大，小根堆是根的底部比顶部数字均小， 其中，对于堆，每一个父节点都有两个子节点，而大根堆和小根堆都可以使用数组来进行存储， 其存储的位置如图所示，而下标标注已在圆圈标注中给出

我们以下面一个大根堆的存储结构为例, 其存储结构如图所示:

12	10	8	6	5	4	7	4	3	2	1

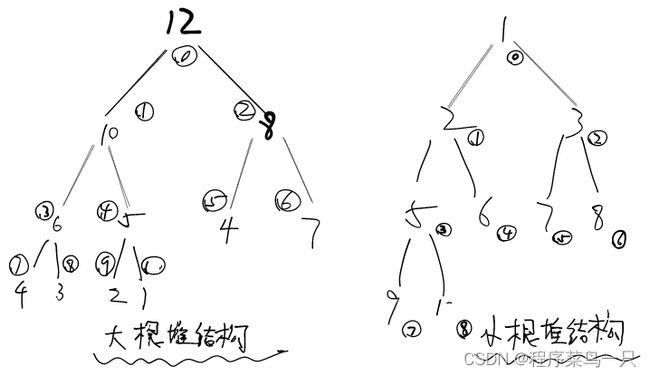
首先我们介绍几个堆的存储特点:
首先下图是一个堆，其中圆圈中的数是堆对应存储数组的下标。树结构可如下图所示:

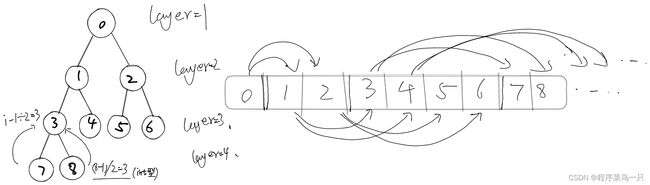
显然由上图可以归纳得出

1. 设子节点的下标为$i$,则父节点的下标为: $(i-1)/2$
2. 设父节点为$j$,求解子节点的下标分别为$2\ast j+1,2\ast j+2$
3. 每一层的首个节点下标为$2^{layer-1}-1$，通过此算法这个可以获取整个树的层数

我们首先假设"维护"一个仅两层的大根堆的过程: 只需将父节点和子节点中最大的值交换即可

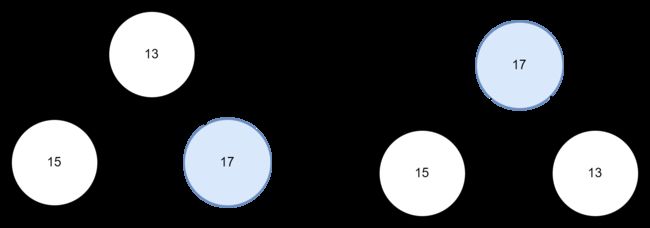
我们以下面的一个三层的无序堆为例，说明通过堆排序寻找数组最大值的过程：

1. 对于一个无序堆想要变成一个大根堆，可以使用自底向上的方法，也即先找到一个末端子节点的值(假设layer3)，并对其父节点维护大根堆，则父节点的值必然是两个子节点中最大的, 则对父节点在layer2上的部分维护完成后(下图第2步)，则下面两层的最大值必然会被放在 layer2中。

2. 然后我们只需要自下向上再维护layer1(图3部分)，则layer1中的值就是整个树的最大值
   
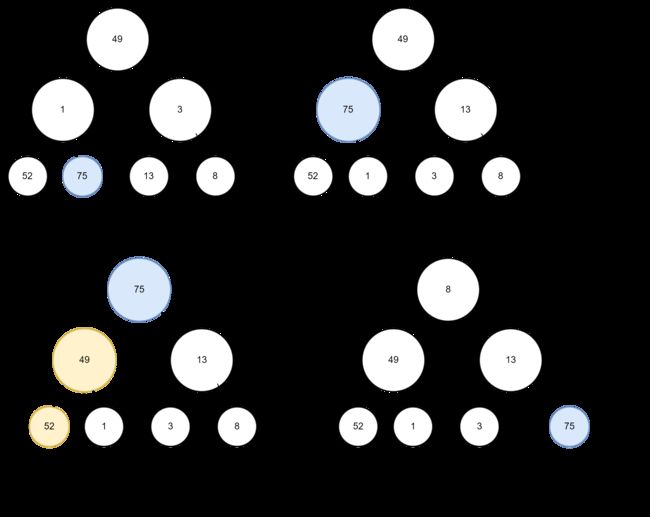
   堆排序的思路如图4， 每一次找到最大的值并与末尾的值交换，则得到了数组中最大的元素。同理得到第二大元素之后，和倒数第二个元素进行交换。 如此反复，最终即可得到升序排序的数组。

补充: 将无序堆转换为大根堆的方式
需要注意的时，在第3步中，虽然最大值已经求出，此时的数组并非大根堆数组(黄色为反例)，如果想要得到大根堆数组，只需对于第一层的每一个子节点，将其分别当成一个堆，每一个堆再次自下而上进行维护过程，得到2,3节点的值， 如此进行循环，即得到了大根堆数组。

堆排序的复杂度较难直接说明，在这里仅说明其复杂度为$O(N\times {\log }_{2}N)$

就堆排序本身而言，在一般情况下，其排序效率上还是比不上快速排序等的排序效率，但是这种方法相对于冒泡和选择排序的方法往往都会好很多

堆排序的cpp代码实现如下：

#include 
using namespace std;

void Show_Array(int A[], int length) {
	for (int i = 0; i < length; i++) {
		cout << A[i] << " ";
	}
	cout << endl;
}

int pow(int a, int b) {  // 代码较少的pow方法
	if (b == 0) return 1;
	int c = 1;
	for (int i = 0; i < b; i++) {
		c *= a;
	}
	return c;
}

// 输入数组的下标，找到所在的层
int FindLayer(int index) {
	int layer = 0;
	int temp = index + 1; // temp 最小为1
	for (; temp != 0; temp/=2) {
		layer++;
	}
	return layer;
}

// 通过递归方法，自底向上整理所有堆，交换对应的下标(通过这个函数整理的堆首元素必定是最大的)
void arange_Heap(int Arr[], int Maxlayer ,int length){
	// 使用循环的方式，通过将根节点向上移动，寻找堆中的最大值
	if (Maxlayer == 1) return; // 不排序，直接返回

	for (int sort_Layer = Maxlayer - 1;sort_Layer > 0; sort_Layer--) {
		// 从该层开始进行排序
		for (int sort_index = pow(2, sort_Layer - 1)-1; sort_index < pow(2, sort_Layer) - 1; sort_index++) {
			int l_index = 2 * sort_index + 1;
			int	r_index = 2 * sort_index + 2;
			// 首先判断子节点和sort_index的大小
			if (l_index >= length);  // 2i+ 1>=length 此时没有左节点也没有右节点，直接返回
			else if (r_index < length) { // 两边都有节点
				int large_index = sort_index;
				if (Arr[large_index] < Arr[l_index]) {  // 记录三个节点中最大值的下标
					large_index = l_index;
				}
				if (Arr[large_index] < Arr[r_index]) {
					large_index = r_index;
				}
				if (large_index != sort_index) {
					int t = Arr[sort_index];
					Arr[sort_index] = Arr[large_index];  // 交换到根节点上
					Arr[large_index] = t;  // 交换两个值
				}
			}
			else{ // 2 * sort_index = length -2, 仅有一个左节点
				if (Arr[sort_index] < Arr[l_index]) { // 如果左节点大于对应节点，则交换
					int t = Arr[sort_index];
					Arr[sort_index] = Arr[l_index];
					Arr[l_index] = t;
				}
			}
		}
	}
}

// 堆排序主调函数
void Heap_Sort(int Arr[], int length) {
	int layer = FindLayer(length);

	if (length == 1) return;
	for (int len = length; len > 1; len--) {
		int max_layer = FindLayer(len - 1);
		arange_Heap(Arr, max_layer, len ); // 通过堆方法找到首元素为最大值
		// 将首元素与末尾对应部分元素交换
		int t = Arr[0]; // l最小为2
		Arr[0] = Arr[len-1];
		Arr[len-1] = t;
	}
}

// 堆排序
int main() {
	int A[13] = { 52,1, 81, 49,75, 13, 8, 9, 12, 17, 63, 76, 3 }; 
	int length = 13;
	Heap_Sort(A, length);
	Show_Array(A, length);
	
	return 0;
}

五、参考资料

参考资料:
[1] 归并排序（分治法）
[2] 排序算法：归并排序【图解+代码】
[3] 快速排序法（详解）
[4] 六大排序算法：插入排序、希尔排序、选择排序、冒泡排序、堆排序、快速排序
[5] 【排序算法】希尔排序（C语言）
[6] 堆排序详细图解（通俗易懂）
[7] 排序算法：堆排序【图解+代码】

六、总结和补充

上述讲到的快速排序，归并排序，希尔排序和堆方法，相较于冒泡和选择排序而言，都是性能非常优越的方法。在时间复杂度上等，都有较良好的性能。

如果想参考其他优越的排序算法，可以自行搜索基数排序，桶排序等等其它的排序算法，如基数排序的时间复杂度为$O(n)$，但是仅仅适用于整数或者有指定位数小数的排序

虽然在c++中，本身具有自带的std::sort()函数，但是排序速度上可能和上述的排序算法有差异，如果想要自行比较，可以复制修改上述代码并进行比较。

这一次算是将比较重要的排序算法进行了一下总结归纳，以后可能会在学习期间更新一些数据结构里面的基本内容。